SESSION 5

MASS TRANSFER - I

Chairman: J. Chato

INTRODUCTION

Pressure-driven fluid convection or filtration flow across the artery wall may promote lipid infiltration,¹ therefore having important implications in the earliest stage of atherogenesis.²

Filtration flow across large arteries has been studied by many investigators, and it is now common knowledge that endothelial lining integrity^3,4 and transmural pressure^5,6 are two major factors affecting filtration flow. However, the filtration rate across the wall of an artery has also been found to depend on the perfusate albumin concentration, by decreasing according to increasing albumin concentration in the perfusion solution.⁷ This dependency has been attributed mainly to a phenomenon called 'concentration polarization' at the blood/wall interface with the macromolecules increasing in concentration from the bulk value towards the interface.⁷

Concentration polarization of macromolecules is influenced by the flow rate, or wall shear rate, and drops when wall shear rate increases.^8,9 Therefore we have reason to believe that the flow rate or wall shear rate may also affect the filtration flow across the artery wall. The previous measurements of filtration flow or hydraulic conductivity of blood vessel walls were made in the absence of blood flow, which is not the case in vivo. In the present study, the filtration rates across the canine carotid artery were measured in vitro under 4 different flow conditions.

MATERIALS AND METHODS

The canine common carotid artery was cannulated with thin stainless steel pipes and then encased in a water tight transparent Plexiglas chamber (Fig. 1). The encased blood vessel segment was perfused with Krebs solution in steady flow. Filtration rates across the walls of the freshly prepared arterial segments were measured using the calibrated glass capillary on the chamber under 4 different experimental conditions: 1) albumin-free Krebs solution under absent flow condition; 2) albumin-free Krebs solution with flow (148 ± 8 ml/min); 3) Krebs solution containing 1.0 g/dl bovine serum albumin under absent flow condition; 4) Krebs solution containing 1.0 g/dl bovine serum albumin with flow (148 ± 8 ml/min).

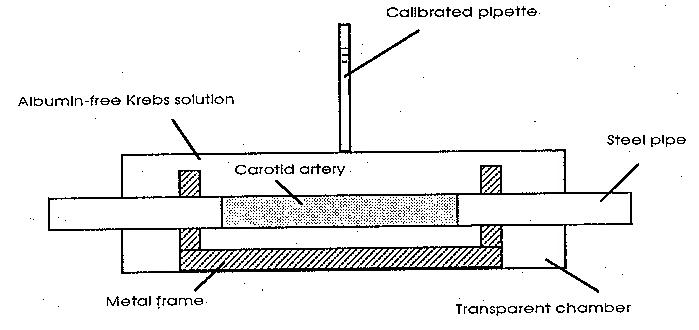
Figure 1. Schematic drawing of the specimen chamber used to measure the filtration rates. The pipette was calibrated by injecting known aliquots of solution.

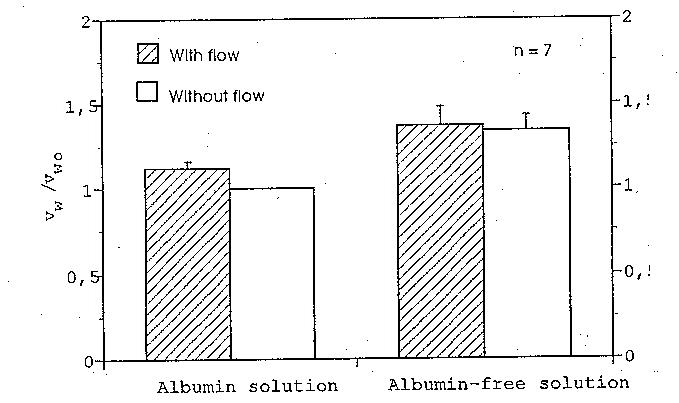
Figure 2. Mean values of the ratios between the filtration rates under different experimental conditions. v_wo is the filtration rate of the albumin solution under absent flow conditions. Note that the fluid flow only affects the filtration rate of the albumin solution; its influence on the filtration rate of the albumin-free solution is not significant.

RESULTS

The mean values of the normalized filtration rates with standard deviations are plotted in Fig. 2. The filtration rate of the albumin solution under a flow rate of 148 ml/min was about 12% higher than that registered under absent flow conditions (p < 0.005). In the case of the albumin-free solution, the statistics showed no significant difference in filtration rate between the flow condition and the absent flow condition (p > 0.01), indicating that the flow did not affect the filtration rate of albumin-free solution across the artery wall.

DISCUSSION

Due to the fact that flow has no effect on the filtration rate across the arterial wall in the absence of albumin, we doubt that the changes in filtration rate were caused by a cellular response to wall shear forces. We do, however, suggest that the increase of filtration rate was basically the result of the decreased luminal surface concentration of albumin. Albumin protein particles on the luminal surface affects the filtration flow twofold: 1. The concentrated protein layer creates a greater osmotic pressure difference across the wall of the tested vessel, thereby lowering the pressure gradient across the artery wall, which is the driving force for filtration flow. 2. Most importantly, albumin particles accumulated on the luminal surface of the test artery can physically block the junctions and pores of the endothelium, hindering the passage of fluid through the wall. The luminal surface concentration of macromolecules is influenced by the flow rate, or wall shear rate, and drops when wall shear rate increases. That is why filtration rate of the albumin solution (but not the albumin-free solution) across the arterial wall increased under flow conditions.

In conclusion, concentration polarization (luminal surface concentration) of proteins or lipoproteins has a significant effect on filtration across the artery wall. Luminal surface concentration of protein particles is wall shear-dependent. Therefore, blood flow or wall shear rate may indeed affect the filtration rate of the artery wall.

REFERENCES

1. Tedgi, A. & M.J. Lerver. 1985. The interaction of convection and diffusion in the transport of ¹³¹I-albumin within the media of the rabbit thoracic aorta. Circ. Res. 57: 865-873.
2. Walton, K.W. 1975. Pathogenetic mechanism in atherosclerosis. Am. J. Cardiol. 35: 542- 558.
3. Vargas, C.B., F.F. Vargas, J.G. Pribyl & P.L.Blackshear. 1979. Hydraulic conductivity of the endothelial and outer layers of the rabbit aorta. Am. J. Physiol. 236: H53-H60.
4. Tedgui, A. & M.J. Lever. 1984. Filtration through damaged and undamaged rabbit thoracic aorta. Am. J. Physiol. 247: H784-H791.
5. Lever, M.J. & N. Sharifi. 1987. The effects of transmural pressure and perfusate albumin concentration on the hydraulic conductivity of isolated rabbit common carotid artery (abstract). J. Physiol. 387: p. 68.
6. Baldwin, A.L., L.M. Wilson & B.R. Simon. 1992. Effect of pressure on aortic hydraulic conductance. Ateriosclerosis and Thrombosis 12: 163-171.
7. Tarbell, J.M., M.J. Lever & C.G. Caro. 1988. The effect of varying albumin concentration on the hydraulic conductivity of the rabbit common carotid artery. Microvasc. Res. 35: 204-220.
8. Blackshear, P.L., K.W. Bartel & R.J. Forstrom. 1977. Fluid dynamic factors affecting particle capture and retention. In The Behavior of Blood and Its Components at Interface. L. Vroman & E.F. Leonard, Eds: 270-279. New York Academy of Science. New York.
9. Deng, X.Y., Y. Marois, T. How, Y. Merhi, M.W. King & R. Guidoin. 1995. Luminal surface concentration of lipoprotein (LDL) and its effect on the wall uptake of cholesterol by canine carotid arteries. J. Vasc. Surg. 21: 135-145.

ABSTRACT

New mathematical models are formulated and analytical solutions are presented for the diffusional release of a solute from a biodegradable drug-impregnated slab matrix in which the initial drug loading c₀ is greater than the solubility limit c_s. A Stefan problem with moving boundaries results from this formulation. An inward moving diffusional front separates the reservoir (unextracted region) containing the undissolved drug from the partially extracted region. The cumulative mass released is determined as a function of time. The ultimate goal of such an investigation is to provide a reliable design tool for the fabrication of specialized implantable matrix/drug combinations to deliver pre-specified and reproducible dosages over a wide spectrum of conditions and required durations of therapeutic treatment. Such a mathematical/computational tool may also prove effective in the prediction of suitable dosages for other drugs of differing chemical or molecular properties without additional elaborate animal testing.

Controlled-release drug delivery is a subject of keen interest world-wide at this time. National and international pharmaceutical concerns and biomedical device developers are actively interested in exploiting this rapidly evolving and potentially lucrative market. Some of the many state-of-the- art applications may conceivable include:

• sustained release of estrogen and progesterone for menopausal women
• programmed release of antibiotics for patients recovering from surgical repair of bone fractures and/or installation of articular prostheses
• encapsulation of ovarian cells which themselves may continue to produce estrogen
• slow release of contraceptive chemicals for both men and women, particularly in third-world countries where the discipline of taking daily doses may be lacking
• drug delivery to targeted organs: e.g. slow release of insulin for diabetics
• encapsulation of pancreatic cells which may themselves trigger the natural production of insulin on a long term self-sustainable basis for diabetic patients.

Recent technical advances now permit one to control the rate of drug delivery. The required therapeutic levels may thus be maintained over long periods of months and years through implanted rate-controlled drug release devices. Two such novel drug delivery systems currently employed are implantable polymeric and ceramic erodible monoliths.

An inward moving diffusional front separates the reservoir (unextracted region) containing the undissolved drug from the partially extracted region. This front is followed by an inward propagating erosion front. The positions of these fronts are not known a priori but must be determined in the course of the solution. The mathematical formulation of such moving boundary problems (Stefan problem) has wide application to heat transfer with melting phase transitions and diffusion-controlled growth of particles, in addition to our topic of controlled-release drug delivery.

Additional applications of an industrial, agricultural or environmental nature, involving the diffusional release of a dispersed or dissolved solute from a polymeric monolith in which a pre- programmed dose-time schedule is necessary, further extend the interest in this problem to international levels. Examples of such applications may include the removal of solvent from polymer solutions during the dry spinning of fibres, photoresist technology and microlithography, diffusional release of pollutants and additives from polymers into the environment and controlled release of agricultural chemicals.

The rate-limiting property of the controlled drug delivery system resides in the design properties of the implanted drug delivery device itself, and is not necessarily dependent upon the physiology of the subject. Drug release kinetics may depend on a number of intrinsic properties of the drug delivery implant: drug solubility, molecular weight and partition coefficient, matrix swelling, osmotic pressures, ion exchange, local electromagnetic force fields, etc. In this work, we focus on two specific properties of the drug delivery system: drug diffusion and matrix erosion. By the term erosion, we mean to denote the process by which material which is intrinsically insoluble in water can be converted into one that is water-soluble. In a pendant chain system for example, one may imagine a drug which is covalently bound to insoluble molecules and is then released by scission of its bonds either by water or by enzymatic action. As the surface of the matrix is exposed to the surrounding extracellular fluids, its structure erodes and the drug impregnated within its walls and pores escapes.

We obtain simplified expressions based upon linearized distributions of drug concentration. These are valid under conditions of pseudo-stationarity; that is, when the velocity of the diffusion front is not too large as to alter concentration distributions too abruptly. Outside the pseudo- stationary range, the diffusion front progresses more rapidly through the matrix medium and the pseudo-stationary approximation upon which the linearized concentration distributions were based may no longer be valid. We have shown that the analytical solutions using linear concentration distributions are accurate to within a few percent of our exact numerically obtained solutions for a wide range of the dimensionless parameters a and b , where a is the ratio between the solubility limit concentration of the drug behind the diffusion front and the initial loading concentration of the drug in the matrix ahead of the diffusion front, and the dimensionless parameter b is the ratio of the erosion front velocity times the initial thickness of the slab divided by diffusion coefficient. The exact numerical results were obtained by a straightforward finite-difference computational solution of the governing equations with given initial and boundary conditions.

Thirty-one cases were computed with the following parameter values: Set 1: three values of b = 0.05; .08; 0.10 with five values of a = 0.08; .10; 0.12; 0.18 and 0.20 (15 possible combinations) and Set 2: four values of b = 0.1; 0.5; 1.0 and 5.0 combined with four values of a = 0.5; 1.0; 2.0 and 10.0. In this range of practical interest, the agreement of the linear approximation with the exact numerical solution for the position and velocity of the diffusion front and the resulting cumulative mass release as a function of time is seen to be very adequate. The analytically derived cumulative mass curves begin gradually to diverge from the exact comptational solutions for a > 0.5.

By adjusting several design parameters characterizing the drug delivery system, one may control the cumulative mass release process in a predictable manner. For example, by incorporating the desired macromolecular drug into the casting of a polymeric matrix, "winding tortuous" pores are created which condition the speed of the diffusion process through a corresponding alteration in the effective permeability of the cast drug-impregnated matrix. By coating the matrix with an impermeable film or membrane, one can slow down the rate of drug release until bioerosion occurs. One may also increase the diffusion rate by raising the ratio of drug loading to solubility limit c_o/c_s.

Many of these considerations, including the shape factor and matrix swelling, can be incorporated into further refined versions of the above models which may then serve as a valuable framework for the design of experimental protocols to test and evaluate the sensitivity of such factors on the cumulative mass release of drug into the body as a function of time. Currently, time- consuming trial-and-error methods are employed in the design of such implants. Using the present approach, an efficient computationally aided tool can be created to design the desired implant in order to release the clinically prescribed dose-time program for specific therapeutic applications ranging from weeks to years in duration.