SESSION 7

CRYOBIOLOGY - I

Chairman: M. Toner

INTRODUCTION

Cryopreservation of cells and tissues require the pre-loading of these systems with chemical additives called CPAs (cryoprotective agents). The addition and removal of CPA from single cells is fairly well understood and can be both measured with microscopy techniques and modeled with irreversible thermodynamics as expressed in the equations of Kadeem-Katchalsky¹. However, there are still several challenges to modeling CPA transport in tissue systems, where unlike the single cell, the membrane is only one of many resistances to transport faced by the CPA which must ultimately enter the cell cytoplasm. In particular, the CPA must be transported through the tissue a certain distance before arriving at a particular cell membrane. This transport and the corresponding cell osmotic excursion, once the CPA effects are felt at a particular cell, are difficult to measure and predict.

The purpose of this work was to obtain suprazero water transport data from the measurement of volumetric shrinkage response of cells within an optically thick whole tissue slice exposed to a hyperosmotic, non-permeating CPA, sucrose. We then try to explain the dynamics of cellular and vascular volume changes by mathematical modeling which includes various resistances to sucrose diffusion in the tissue matrix.

THEORY AND MODELING

Two models for the transport of sucrose through the tissue via an extracellular/ vascular pathway were developed using a Krogh cylinder approach. For a one dimensional Cartesian case the general species transport equation can be written

The first model proposes that sucrose transport into the tissue and subsequent cellular changes can be interpreted by an effective diffusivity of species 1, sucrose. Since there is no reaction, equation 1 then reduces to

A second model was proposed which assumes that water entering the vasculature from cellular dehydration due to increased sucrose concentration leads to a bulk convective flux towards the boundary of the slice. The Starling's equation is used to describe cellular dehydration due to osmotic pressure difference created by sucrose in the vasculature similar to the freeze induced dehydration as previously described³. The diffusion of sucrose into the tissue is thus coupled to convection of water out of the tissue, due to dehydration. Equation 1 is rewritten for sucrose, with no reaction, and it reduces to:

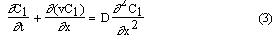
The two models are implemented numerically using a finite difference discretization scheme. Boundary conditions included a constant sucrose concentration at one boundary and symmetry at the centerline. The initial condition was zero sucrose concentration throughout the tissue.

MATERIALS AND METHODS

Experiments were performed on freshly excised livers from Sprague Dawley male rats (175- 200g), (Harlan Sprague Dawley, Inc., Indianapolis, Indiana). Thin (~500µm) tissue slices were subject to a hyperosmotic sucrose solution at 2°C (0.3M or 0.6M) for different time periods, and slam frozen immediately after the experiment in liquid nitrogen. The tissue samples were then freeze substituted,² embedded in resin, sectioned and imaged under a light microscope fitted with a digitizing system³.

RESULTS AND DISCUSSION

Image analysis of cellular and vascular/extracellular volumes was performed with NIH Image software^TM (NIH, Bethesda, MD) to ascertain cellular and vascular volume over time. Figure 1 shows the morphology of the liver tissue after 0, 5, 15, and 30 minutes of exposure to 0.6M sucrose solution at 125µm from the constant sucrose concentration boundary. As shown in the figure, individual hepatocytes appeared as a clump of dark stained polygonal structures with gray round nuclei. The large white continuous areas between the cells correspond to the vascular/extracellular space (predominately vasculature, 10.6% plus some interstitium, 4.9%). The micrograph shown in Figure 1A gives a view of the liver cells in their control (normal) size prior to sucrose dehydration. The micrographs in Figure 1(B, C, D) demonstrate the dehydration trend exhibited by the continuous reduction in the areas of the cells as exposure time to hypertonic stress is increased. In addition there was a change in the vascular volume too (denoted by the white regions in the micrograph).

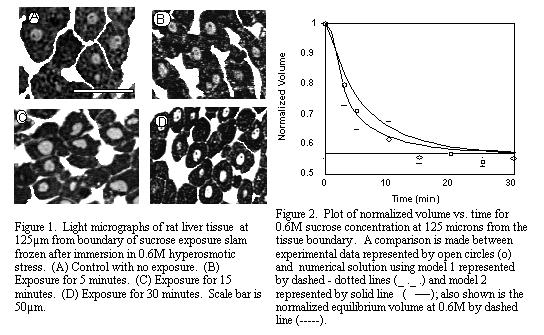
Figure 2 represents a comparison between the experimental and numerical data for 0.6M sucrose at 125µm from the tissue boundary. The normalized cell volume on the y-axis is plotted against minutes of immersion in the hypertonic sucrose solution on the x-axis. Experimental data is represented by open circles, numerical solution using the first model is represented by a dashed- dotted line, where D_eff was estimated by the eye and had R² > 0.97, and the normalized equilibrium volume for a cell exposed to hypertonic 0.6M sucrose environment by a dashed line. D_eff jumps from a value of 0.16D_sucrose at 0.3M (data not shown) to 0.33D_sucrose at 0.6M. These changes in effective diffusivity may be a reflection of the varying void fraction and tortuosity of the tissue during cellular dehydration and vascular engorgement, thereby changing the effective diffusivity⁴. The incorporation of these geometric changes inside the tissue appear to play an important role in the hindered transport of sucrose and need to be incorporated into future modeling attempts.

The second model is represented on the graph by a solid line. It tries to explain the hindered diffusion of sucrose and corresponding cellular shrinkage in a tissue, by incorporating the effect of convecting water which leaves the cells. The model captures the nature of the volumetric shrinkage of the cells, being able to predict them within the error bars of the experimental value. However, the 0.6M case underpredicts the volumetric shrinkage response in contrast to the results obtained from 0.3M sucrose (data not shown), where volumetric shrinkage is overpredicted. This may be an indication that factors in addition to convection, such as vascular compliance, need to be incorporated for better prediction of the experimental results in future models.

CONCLUSION

Transport of a non-permeating CPA in liver tissue was studied by experimental and theoretical techniques. The system consisted of a 20mm x 15mm x 500µm (thick) slab of liver tissue which was exposed to culture media and hyperosmotic sucrose (0.3 or 0.6M) at the boundary. The volumetric changes of cell and vascular spaces within the tissue slab at 125µm from one of the symmetric boundaries was studied by slam freezing followed by freeze substitution microscopy. The experimental data was then theoretically investigated using two models; one based on an effective diffusion coefficient for sucrose, and another which incorporated the convective flux of water out of the cells (and the tissue) while sucrose diffuses in. We estimate the effective diffusion of sucrose as 16-33% of the actual diffusivity of sucrose in bulk water. The role of convection of water out of the tissue is against the flow of sucrose and appears to be important in reducing the effective diffusivity of the sucrose. Moreover, vascular compliance, porosity and tortuosity are important factors that need to be considered while modeling transport in tissues.

REFERENCES

1. Mcgrath, J.J. 1988. Chapter in Low Temperature Biotechnology: Emerging applications and Engineering contributions, J.J. McGrath and K.R. Diller eds, ASME BED 10: 273-330.
2. Robards, A.W., & Sleytr, U.B. 1985. In Low Temperature Methods in Biological Electron Microscopy. (Chapter 7) Elsevier, 10.
3. Pazhayannur, P.V., & Bischof, J.C. 1997. Measurement and simulation of water transport during freezing in mammalian liver tissue, ASME Journal of Biomechanical Engineering 119: 269-277 .
4. Geankoplis, C.J. 1993. Transport Processes and Unit Operations, Prentice Hall, Engelwood Cliffs, N.J., 3rd. ed.: 412-413.

   ---

   ^a This work was supported by a grant from Whitaker foundation to JB. ^c Address for correspondence: Department of Mechanical Engineering, University of Minnesota, Minneapolis, MN, 55455, USA. Phone, 612-625-5513; fax, 612-624-5230.

   ---

   ANALYSIS OF MASS TRANSPORT DURING
   WARMING OF CRYOPRESERVED CELLS
   Alexander V. Kasharin and Jens O.M. Karlsson

   Department of Mechanical Engineering, University of Illinois, Chicago, Illinois 60607, USA

   As a first step towards developing mechanistic models of damage to cryopreserved cells during the warming process, an analysis of water transport during warming was undertaken. With the aim of identifying regimes in which conventional two-compartment, membrane-limited water transport models will be valid for predicting cell dehydration/rehydration during warming, the Peclet number was evaluated. Simulations showed that Pe » 1 during the early stages of warming, indicating that transport was rate-limited by diffusion to and from the membrane. However, by comparing the time-scale of transport to the time-scale of the warming process, it was possible to identify conditions in which the membrane- limited transport model would yield adequate predictions in diffusion- dominated regimes. Simulations suggested that a membrane-limited model would fail during slow warming of rapidly cooled cells, but that it would perform adequately if cooling was slow, or if warming was rapid.

   ---

   METHOD OF DESIGNING PRE-FREEZING PROTOCOL IN
   CROYOPRESERVATION OF BIOLOGICAL MATERIALS

   Ryo Shirakashi^a and Ichiro Tanasawa^b

   ^a Institute of Industrial Science, University of Tokyo, 7-22-1 Roppongi, Minato-ku, Tokyo 106, Japan ^b Tokyo University of Agriculture and Technology, Faculty of Engineering, Mechanical Systems Engineering, 2-24-16 Naka-cho, Koganei, Tokyo 184, Japan

   ABSTRACT

   Procedures of determing the pre-freezing protocol in cryopreservation of biological materials are discussed. In order to cryopreserve biological materials, especially tissues with large sizes, the concentration of cryoprotective agents (CPAs) should be high enough after pre-freezing process, because a high concentration CPA solution can be vitrified a rather low cooling rate. In the pre- freezing process, the concentration of CPA is raised gradually to avoid osmotic stress. In this paper, a conventional method of designing the pre-freezing protocol is proposed. The rate of increase of the concentration of CPA can be calculated on the basis of Kedem-Katchalsky equations using the membrane permeabilities, Lp, w and s. Optimal protocol can be determined by calculating a process in which the normalized volume of the cell is kept constant whole through the process.

   INTRODUCTION

   To cryopreserve successfully a biological material, especially a tissue with large size, one would rather avoid the deleterious effects of cooling rate. When the cooling rate is lower, the cells composing biomaterial suffer from solution effect or mechanical stress caused by extracellular ice crystals. On the other hand, when the cooling rate is higher, intracellular ice is nucleated which might break the cell membrane mechanically. These phenomena suggest that only a certain narrow range of cooling rate permits high viability of cryopreserved cells. Many researchers use CPA to get over this trend. Vitrification is the ideal method, because the deletrious effects of cooling rate in the freezing process is negligeble by avoiding ice nucleation. Fahy, MacFarlane, Angell and Meryman¹ showed that the glass transition occur even at a low cooling rate, if the concentration of CPA is high enough (for glycerol around eutectic point). But, to introduce such a high concentration CPA into cells, as well as into a tissue, is so difficult that efforts such as searching new CPA (low viscosity, low toxicity), adding a pressure during freezing process are made to reduce the concentration of CPA which can vitrify. In any case, CPA should permeate through the membrane of cells without suffering from osmotic shock. To avoid the possible effect of the osmotic pressure induced by a sudden change of concentration of CPA, it might be effective to raise the concentration of CPA gradually². Moreover, pre-freezing protocol should be finished in a short period, because the longer the pre-freezing period, the more degenerate biomaterial might be .

   This paper proposes a method to design pre-freezing protocol using the membrane permeabilities and size of cells, using Kedem-Katchalsky (K-K) equation as fundamental equation. Similar researches were made by R. Levin and T.W. Miller³. We tried to simplify the method of design, moreover, to assess whether the designing principle is usable by applying the method to endothelial cells of porcine arteries.

   DESIGN CONCEPT

   As the large difference of concentration between intracell and extracell gives osmotic stress, it might be effective to change concentration of CPA continuously. By solving K- K equation numerically, the volume change of a cell can be predicted. Optimized profile can be calculated by keeping b_min larger than b_cri which is the normalized equilibrium volume. According to the numerical calculation, the volume flux across the membrane is nearly 0 through the pre-freezing process, that is, K-K equation can be simplified to eqs. (1) as below.

   C^o_a=C^o_a0+[w_aRT(1-b_lim)]/[s_a(b_lim-e)²]*C¹_e0*(S₀/V₀)*(t-t_min) (1)

   It is clear that among three membrane permeabilities, w_a and s_a is important for optimizing the rasing rate of concentration.

   PRE-FREEZING PROCESS OF PORCINE ARTERIES

   To examine fundamental equations for design, porcine arteries were immersed in glycerol solution of different concentrations, followed by estimation of viabilities of endothelial cells. Two kinds of protocols were taken place. Viabilitiy which was assessed by means of dye-exclusion test⁴ after each pre-freezing process is compared with corresponding b_min calculated. The result shows a possibility of predicting damage depends on pre-freezing protocol, so that design of optimal profile for pre-freezing process might be possible. However, estimation of damaged cells should be quantified more clearly, and also more reliable values of the membrane permeabilities and critical cell volume b_cri are required.

   NOMENCLATURE

   C : Concentration (mol/m³)
   b: Cell volume ratio (m³³)
   R : General gas constant (J/(mol K) )
   S :Surface area (m²)
   t : Time (sec)
   T : Temperature (K)
   V : Volume (m³)
   J : Flux through cell membrane ( mol/m², m³/m² )
   Lp : Hydraulic conductivity (m³/(N sec) )
   w: Solute permeability coefficient (mol/(N sec) )
   s: Reflection coefficient
   e: Non-osmotic volume fraction at noramilized osmolarity
   I : Level of brightness
   E : Mean value
   V : Deviation
   

   Subscript and Superscript

   a : Cryoprotective agent
   e : Electrolyte
   o : Extracell
   i : Intracell
   0 : Initial state
   V : Volume
   cri : Critical value
   lim : Minimum limit value
   min : Minimum
   rex : Relaxation
   x : Axis along radius direction of a artery
   y : Axis along axial direction of a artery
   

   REFERENCES

   1. Fahy, G. M., D. R. McFarlane, C. A. Angell & H.T. Meryman. 1984. Cryobiology 21: p.407
   2. Fahy, G. M., & S.E. Ali. 1997. Cryobiology 35: p.114
   3. Levin, R. L., & T.W. Miller.1997. Cryobiology 18: p.32
   4. Imahori, K., & T. Yamakawa et al. Eds. 1990. In Dictionary for Biochemistry (Seikagaku - jiten), 2nd Ed., published by Tokyo kagaku do-jin : p.576, p.934 ( in Japanese)