|
POSTER SESSION 1
HEAT LOSS AND LIQUID STEEL FLOW IN METALURGICAL LADLES DURING HOLDING PERIOD IN CONTINUOUS CASTING
Eliana Ferreira Rodrigues*, Eduardo Bauzer Medeiros**, Renato Minelli Figueira***
*DETEF-Escola de Minas - UFOP,**DEMEC - UFMG, ***DEMET - UFMG,
** Av.Antônio Carlos 6627, 31270-901, Belo Horizonte, MG, BRAZIL,
FAX: (+)(55)(31) 443-3783, email: FLUGZBAU@ORACULO.LCC.UFMG.BR
INTRODUCTION
In the steel industry temperature control is of crucial importance to the quality of the final product. This temperature must be controlled to tight limits, particularly in the case of the liquid steel supplied to a continuous caster via a tundish. Too high temperatures result in energy wastage and poor quality steel. Low temperatures cause blockages and skull formation. Control of ladle temperature appears to be the most important factor, governing the continuous casting process. Whilst it is clear that a general estimation can be obtained with the help of a "conventional" heat balance, more accurate results can only be obtained if other phenomena, particularly temperature stratification inside the ladle, are taken into account.
In the present work a model is developed, considering transient fluid flow and heat transfer in the ladle melt during holding, which is also essential for determining the influence of the slag cover.
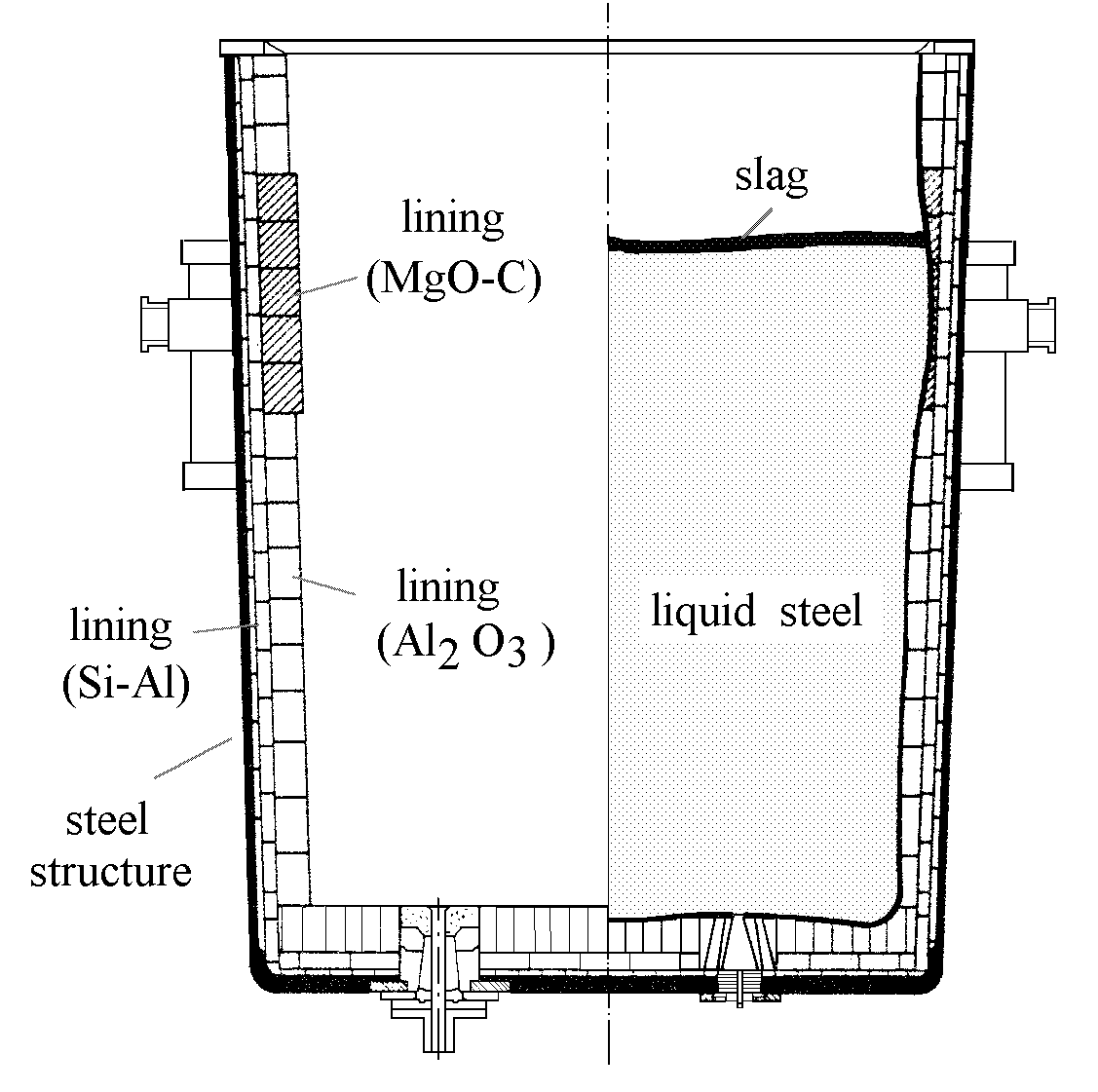
Figure 1 - Sketch of a typical ladle.
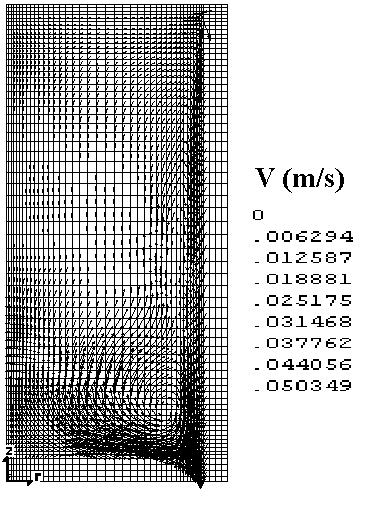
Figure 2 - Velocity 5 minutes after gas stirring.
METHOD
The ladle is assumed to be a cylinder of radius R (= 1.675 m), with negligible (practical) wall inclination, containing steel to a depth H (= 4.0 m). Since the variations in temperature and turbulent fluid flow in the angular (q) direction is negligible, the relevant equations need only to be solved in the radial and vertical direction (r, z). The simulation begins with an assumed homogeneous and steady state ladle full of molten steel. Heat is transferred from the steel to the refractory linings, considering on top either a thin slag layer or a thick (insulating) layer, the latter results shown here.
The partial differential equations governing the heat transfer and fluid flow inside the liquid steel during the holding period can be expressed as:
 (1) (1)
where Gf and Sf are a generalized diffusion coefficient and generalized source term, respectively, for the specific variable f .

In the above equation, µ ef , is the effective turbulent viscosity calculated by means of the standard k-e model. The values of the various constants in the turbulence model follow the recommendations of Launder and Spalding1.
Two dimensional transient heat conduction can be conveniently used to describe the temperature profile in the lining:
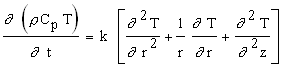 (2) (2)
Equations (1) and (2) have been solved numerically by means of an "ANSYS" and FLOTRAN/F.E.M. code, considering a constant heat conduction coefficient, density and specific heat ( K, r , cp) for each refractory type, and varying melt temperature (K, r and m ).
Boundary Conditions: No slip boundary conditions have been assumed for the steel/lining interface, resulting in zero values for k and e , and the velocities ur and uz. The normal velocity components ant the normal gradients of the parallel velocity components, turbulence energy, and energy dissipation rate were set at zero at both the central symmetry axis and at the top.The velocities parallel to the walls and the turbulence quantities at the near wall nodes have been evaluated using standard logarithmic wall functions1. The heat losses through the thermal boundary layer has been determined considering conduction heat loss through the wall and natural convection in addition to radiation heat transfer at the outside of the walls. Appropriate heat transfer correlation were obtained from2. An average flux of 12.5 kW/m2 has been assumed for both the side and bottom walls, together with an average 1853 K liquid steel temperature. The initial velocity has been considered to be zero. The heat flux at the top has also been set to zero (for the given example) corresponding to the thick skull layer situation.
RESULTS AND CONCLUSIONS
Figures 3 and 4 show a set of typical results corresponding to 20 minutes after the initial time (which is set right after the end of inert gas stirring). For each set of results, typically, 1500 iterations were carried out. When compared to Figure 2, where recirculation is noticeable, with stronger effects near the junction of the bottom to the side wall, it can be observed that recirculation has been reduced. The temperature profile indicates a pronounced stratification after 20 minutes, the temperature gradient being strongly affected by the wall proximity, a fact which is also apparent in the velocity profile. Not surprisingly, viscosity parameters show a pronounced variation near the wall. Perhaps the most relevant fact is that these parameters show what are the exact properties of the molten, and therefore what properties can be expected for the end product.
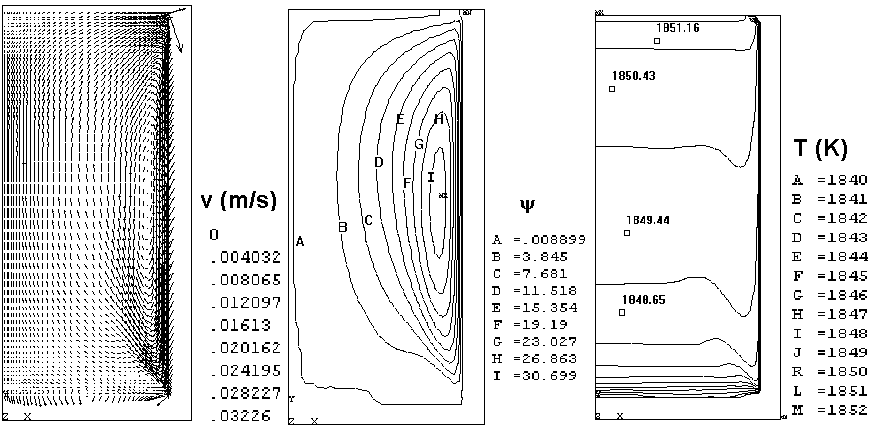
Figure 3 - Velocity, stream funcion and temperature profiles, 20 min after the end of inert gas stirring
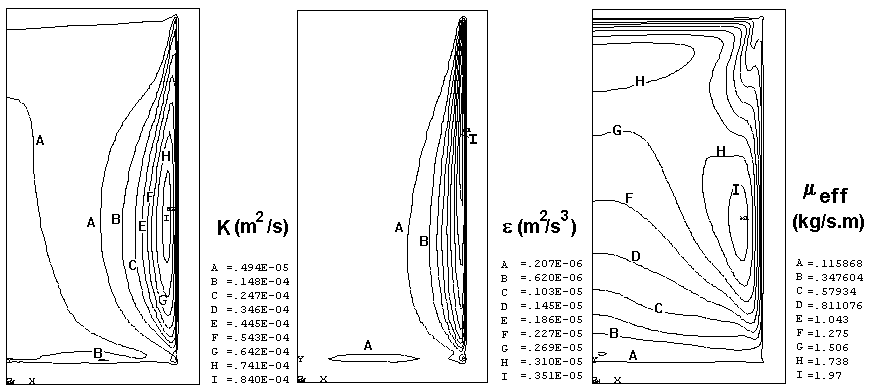
Figure 4 - Kinetic energy k, Rate of Kinetic energy dissipation e , and viscosity m , 20 min after the end of inert gas stirring.
These results are being presently compared with values measured in industry, and simulation data3,4 from the literature. They show good agreement with these sources, strongly hinting at the feasibility of this technique.
REFERENCES
- Launder, B.E. and Spalding, D.B., The Numerical Computation of Turbulent Flows, Computer Methods in Applied Mechanics and Engineering, vol. 3, 1974, pp. 269-289.
- Chakraborty, S. and Sahai, Y., Effect of Slag Cover on Heat Loss and Liquid Steel Flow in Ladles before and during Teeming to a Continuous Casting Tundish, Metallurgical Transactions B, vol. 23B, April, 1992, pp. 135-151.
- Austin, P.R., Camplin, J.M., Herbertson, J. and Taggart, I.J., Mathematical Modelling of Thermal Stratification and Drainage of Steel Ladles, ISIJ International, vol. 32, no. 2, 1992, pp. 196-202.
- Ilegbusi, O,and Szekely, J., Melt Stratification in Ladles, ISIJ International, 1987, vol. 27, pp.563.
COMPUTATIONAL STUDY OF TURBULENT NßXED CONVECTION IN VERTICAL FLAT DUCT UNDER OVERPOWER TRANSIENT
A. Cihat BAYTAS1 and A. Rüstem ASLAN2
l ITU, Institute For Nuclear Energy, 2 ITU, Faculty of Aeronautics and Astronautics ,
80626, Maslak, ISTANBUL,TURKEY
baytas@sariyer.cc.itu.edu.tr
aslanr@sariyer.cc.itu.edu.tr
INTRODUCTION
The mixed convective flow between parallel plates is encountered in various engineering applications such
as building elements, solar collectors, electronic components cooling and nuclear reactors which especially
use plate type fuel elements. Many studies have been published on convection in vertical flat duct. Thermal
boundary conditions of uniform wall heat fluxes and uniform wall temperature were considered. In this
investigation, thermal boundary condition of uniform symmetric and asymmetric boundary conditions are
considered. In addition to this, the overpower transient wall conditions have been investigated and its
effect on velocity and temperature field is also explored. Overpower transient variations of wall
approximates the accident conditions of various types that are nuclear reactor accidents, abnormal
condition of electronic cooling, etc.
The main focus of the present investigation is to consider the unsteady turbulent mixed convection in a flat
duct containing uniform heat flux on the wall. First, the unsteady flow equations are solved until a steady
state is reached. Then, it is assumed that the wall heat fiux is suddenly increased exponentially to simulate
the abnormal condition. For simplicity, we approximate the power production at the walls by
q''(t) = qo''(t) exp(t/R)
where q'' is time dependent wall heat flux and qo'' is steady state wall heat flux value, t is time and R is
period.
MATHEMATICAL FORMULATION AND SOLUTION PROCEDURE
Flow and thermal characteristics in a vertical flat duct can be considered as two- dimensional when the
plate depth is large enough and the effects on the flow are negligible. When the streamwise heat
conduction and viscous diffusion are negligible the mixed convection problem can be represented using
the Parabolized Navier Stokes equationsl. The non dimensional form of the governing equations are
obtained for an incompressible flow and Bossinesq approximation.
The governing equations are solved using a finite difference method based on LSOR. A non-uniform
grid which clustered toward the walls is employed to resolve the sharp gradients present near the
walls. The grid lines are also clustered at the entrance of the duct. The turbulence is modeled
using the Baldwin-Lomax algebraic turbulence modell .
The temperature and velocity fields are obtained for various Gr/Re numbers. The results compare well
with the available literature2,3 . Wall capacity effect on the unsteady local Nusselt number during various
heating conditions and the dimensionless interfacial heat flux are also investigated.
The above analysis is performed for various period, R, values. The effect of various period values on
the temperature and velocity fields and heat transfer characteristics are also analysed.
REFERENCES
- Aslan, A.R., "Parabolised Navier-Stokes Methods for Ducted Flow Systems", von Karman Institute Lecture Series,1991-O1, Computational Fluid Dynamics, Rhode-St-Genese, Belgium,1991.
- Lin, T.F. , Yin, C.P. and Yan, W.M., "Transient Laminar Mixed Convective Heat Transfer in a Vertical Flat Duct", Transaction of the ASME, Journal of Heat Transfer, Vol.113, pp384- 390, May 1991.
- Hung, Y.H., Tsai, K.J. and Sheu, F.C., "Turbulent Mixed Convection in Vertical Parallel Plates with Asymmetrical Isoflux Heating", HTD-Vol. 213, Fundamentals of Mixed Convection, pp.21-29, ASME 1992.
NATURAL CONVECTION IN A CLOSED THERMOSYPHON
S.S. Leong
School of Mechanical and Manufacturing Engineering
The University of New South Wales
Sydney, Australia 2052
ABSTRACT
Natural convection in vertical cylinders with the lower half heated and the upper half cooled has practical application in the preservation of permafrost beneath buildings in ice-bound regions and the cooling of turbine blades. A knowledge of the flow pattern and heat transfer within the cylinder is important for optimising processes. Numerical solutions of the three-dimensional equations for buoyancy driven flows in a closed thermosyphon are presented. The governing non-linear coupled equations (energy and vorticity-vector potential) are approximated using finite differences. The energy and vorticity transport equations are solved using the Samarskii-Andreyev ADI scheme. A fast Fourier transform algorithm is used to solve the elliptic partial differential equations. Solutions are presented for an aspect ratio (length to radius) of 4, Prandtl number (Pr=100) and Rayleigh number (based on the radius) 100 < Ra < 100000.
GOVERNING EQUATIONS
The lower half of the vertical cylinder is heated and the upper half is cooled. Using R and 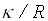 (where k is the fluid thermal diffusivity) as scaling factors for the length and velocity respectively and Boussinesq approximation, the energy and vorticity transport equations are given by (where k is the fluid thermal diffusivity) as scaling factors for the length and velocity respectively and Boussinesq approximation, the energy and vorticity transport equations are given by
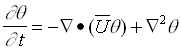 (1) (1)
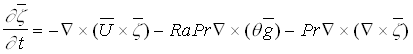 (2) (2)
The vector potential field 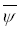 is given by is given by
 (3) (3)
and the velocity vector 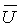 is solved using is solved using
 (4) (4)
NUMERICAL SOLUTION
A uniform mesh consisting of  discrete points in the discrete points in the  , ,  and and  directions respectively is superimposed on the solution domain so that the radial mesh points are given by directions respectively is superimposed on the solution domain so that the radial mesh points are given by 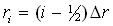 for i=1,2,3,...L; the azimuthal mesh points are given by for i=1,2,3,...L; the azimuthal mesh points are given by  for j=1,2,3,...M and the axial mesh points are given by for j=1,2,3,...M and the axial mesh points are given by 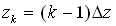 for k=1,2,3,...N, where for k=1,2,3,...N, where 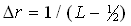 , ,  and and 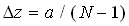 . Details of the solution procedure are reported by Leong. To reduce computational requirement, this paper will present results for an aspect ratio (length to radius) of 4. . Details of the solution procedure are reported by Leong. To reduce computational requirement, this paper will present results for an aspect ratio (length to radius) of 4.
RESULTS
Figure 1 shows the temperature distribution in the vertical midplane ( =0º and 180º), when Ra=1000, 5000 and 50000 and Figure 2 shows the contour plots of =0º and 180º), when Ra=1000, 5000 and 50000 and Figure 2 shows the contour plots of 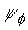 in the same vertical midplane. At Ra=1000, fluid does not cross the mid-height plane and heat is transferred between the two halves by conduction. When Ra=5000, two streams of fluid crosses the mid-height plane. Figure 1(b) shows the temperature distribution in the vertical plane where the two streams of fluid cross the mid-height plane, and Figure 2(b) shows the contour plots of in the same vertical midplane. At Ra=1000, fluid does not cross the mid-height plane and heat is transferred between the two halves by conduction. When Ra=5000, two streams of fluid crosses the mid-height plane. Figure 1(b) shows the temperature distribution in the vertical plane where the two streams of fluid cross the mid-height plane, and Figure 2(b) shows the contour plots of 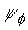 in the same vertical plane. Figure 3 shows the vertical velocity profile of the two streams of fluid. The number of streams of fluid is increased to six at Ra=50000. Figure 4(b) shows three ascending streams and three descending streams. in the same vertical plane. Figure 3 shows the vertical velocity profile of the two streams of fluid. The number of streams of fluid is increased to six at Ra=50000. Figure 4(b) shows three ascending streams and three descending streams.
These numerical solutions are in agreement with the experimental results obtained by Japikse et al.
CONCLUSIONS
The numerical results show that the complex three-dimensional natural convection in a closed thermosyphon observed experimentally can be predicted numerically.
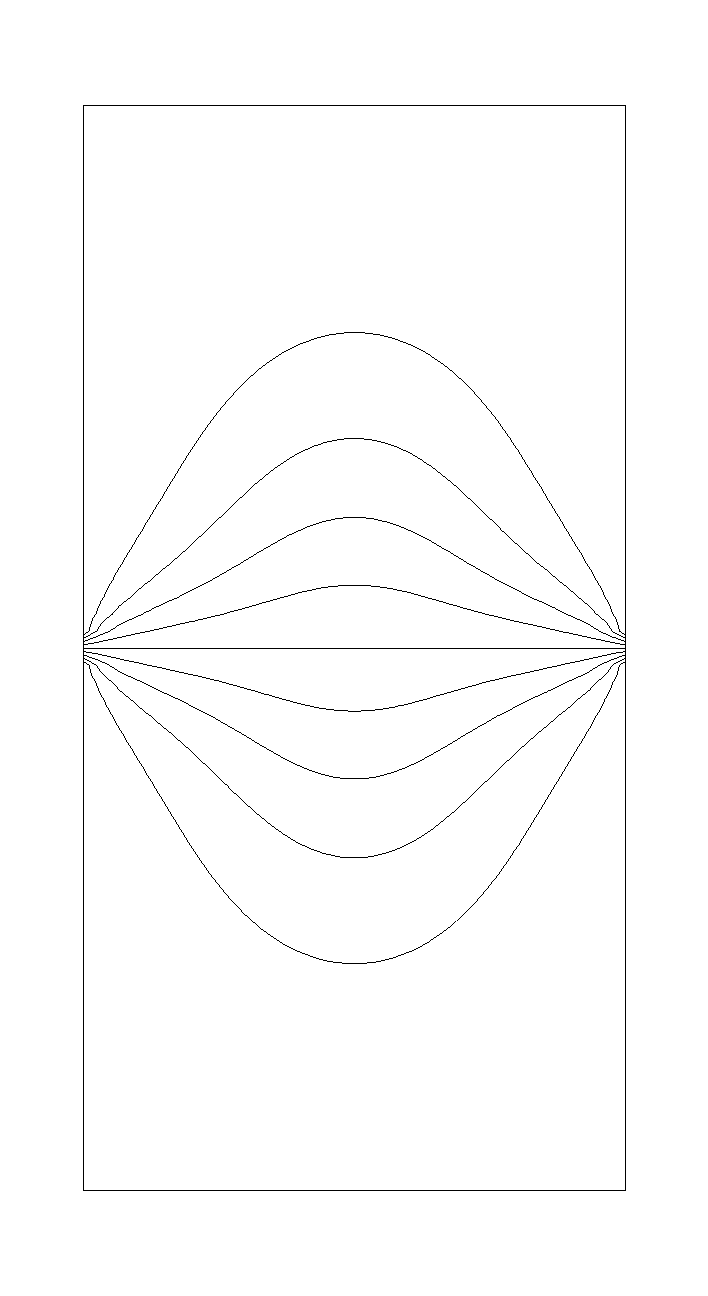  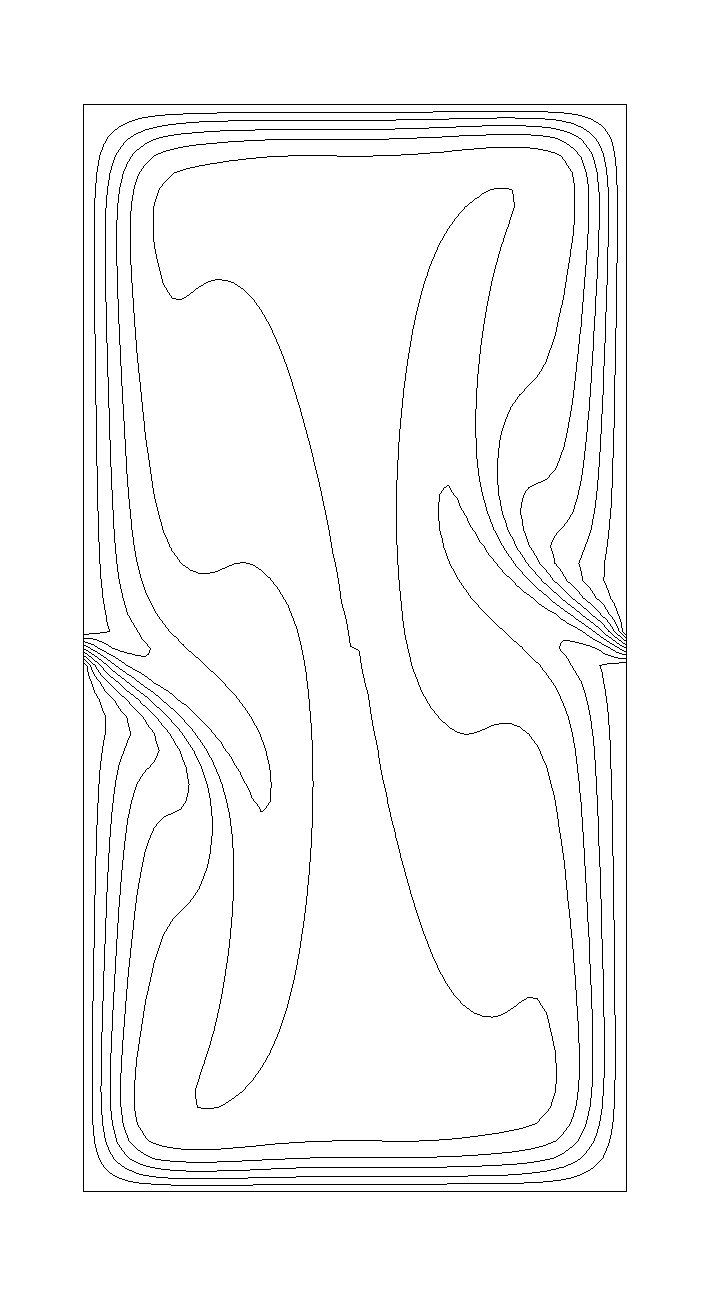
Fig. 1. Temperature distribution in the vertical midplane ( =0º and 180º) for =0º and 180º) for
(a) Ra=1000, (b) Ra=5000 and (c) Ra=50000
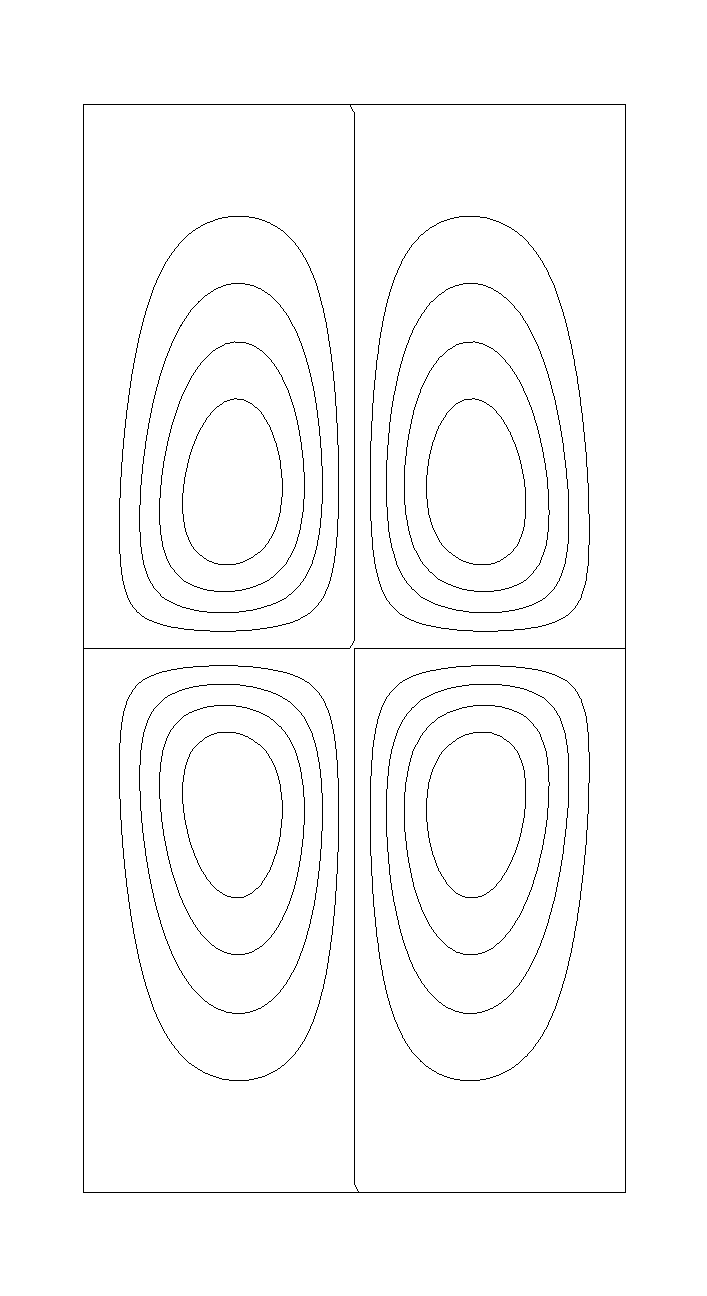 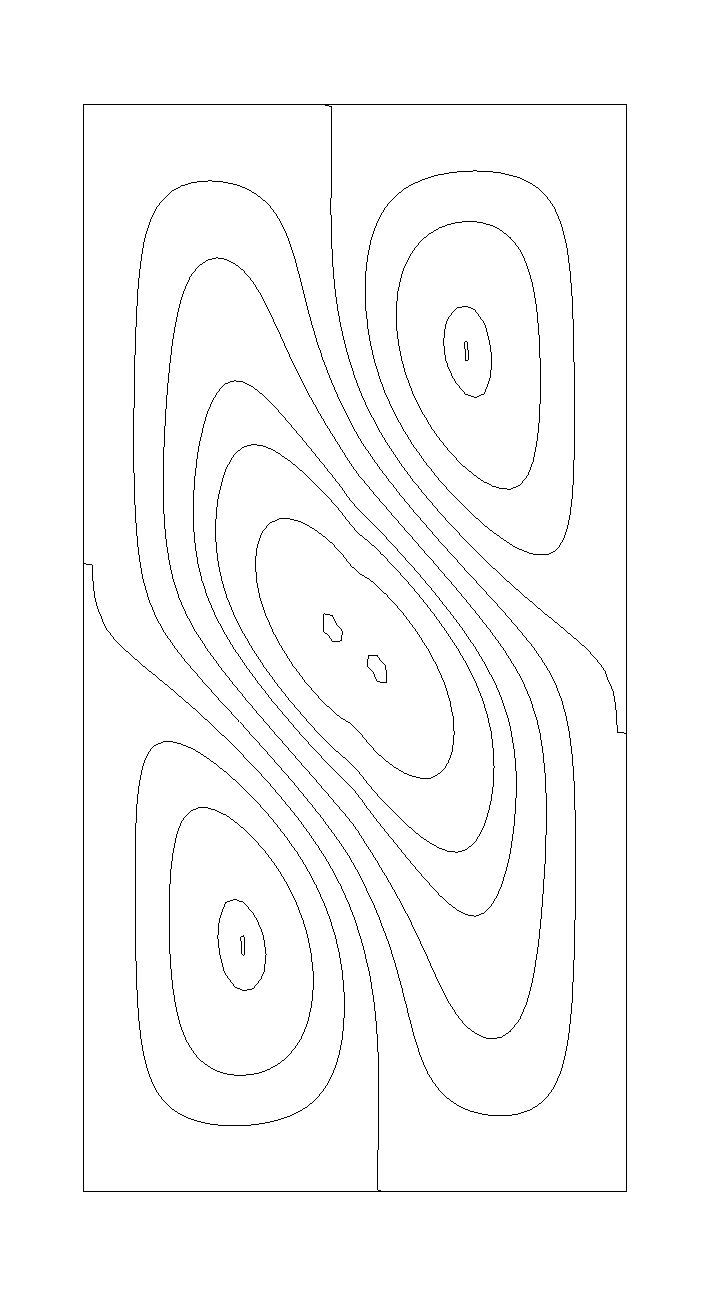 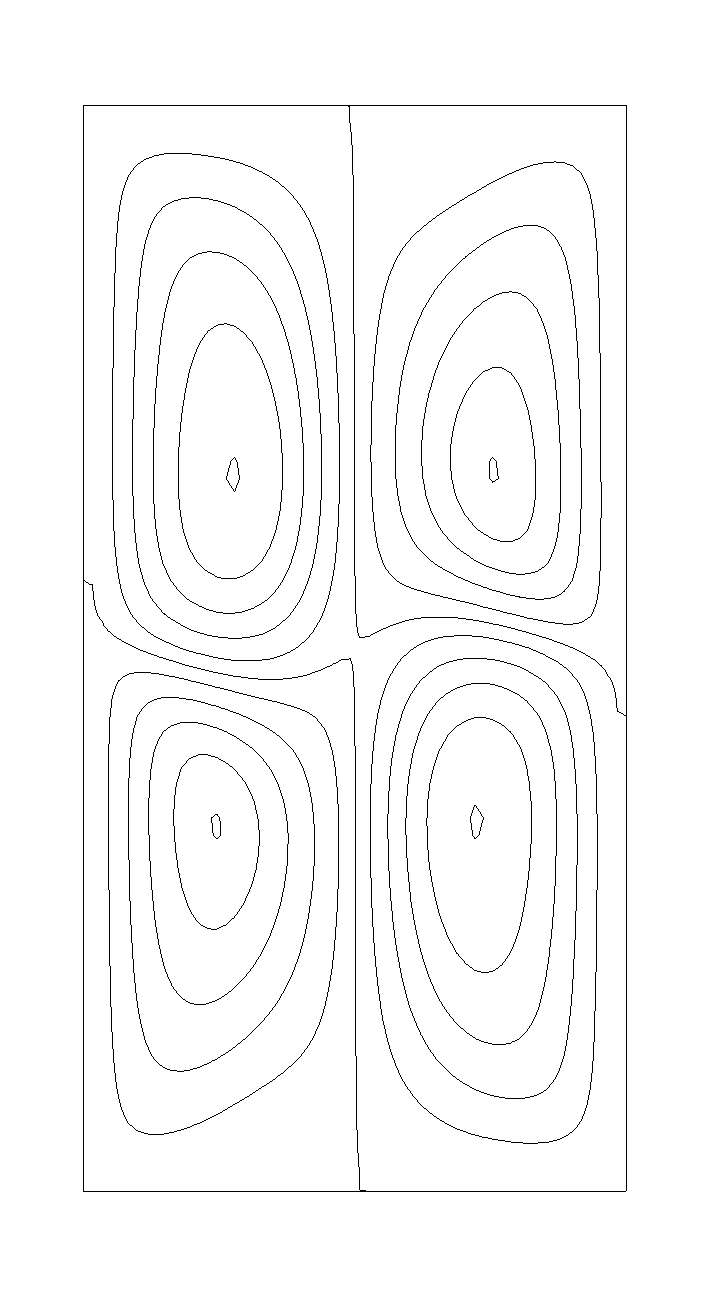
Fig. 2. Contour plots of 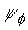 in the vertical midplane ( in the vertical midplane ( =0º and 180º) for =0º and 180º) for
(a) Ra=1000, (b) Ra=5000 and (c) Ra=50000
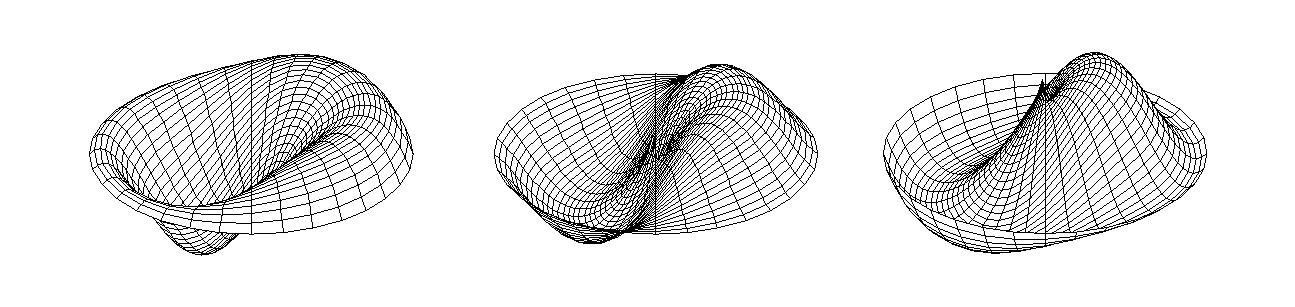
Fig. 3. Vertical velocity in the horizontal plane when Ra=5000 at
(a) 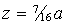 , (b) , (b) 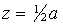 and (c) and (c) 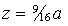
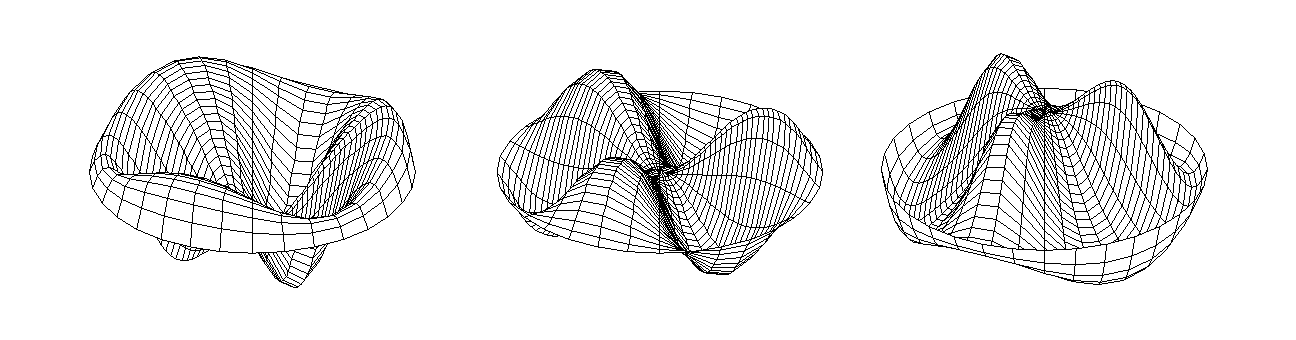
Fig. 4. Vertical velocity in the horizontal plane when Ra=50000 at
(a) 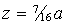 , (b) , (b) 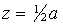 and (c) and (c) 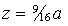
REFERENCES
- Leong, S.S., Natural Convection In Cylindrical Containers, PhD Thesis, University of N.S.W., Kensington, Australia, 1983.
- Japikse, D., Jallouk, P.A. and Winter, E.R.F., 1971, Single-phase transport processes in the closed thermosyphon, Int. J. Heat Mass Transfer, Vol. 14, pp 869-887, 1971.
TRANSIENT INTEGRAL TRANSFORM SOLUTION OF NATURAL CONVECTION IN ENCLOSURES
M. A. Leal and R M. Cotta
Laboratório de Transmissão e Tecnologia do Calor - LTTC
Mechanical Engineering Dept. - Universidade Federal do Rio de Janeiro
EE/COPPE/UFRJ
Cidade Universitária - Cx. Postal 68503 - Rio de Janeiro - RJ - 21945.970 - Brazil
ABSTRACT. This paper deals with transient natural convection within two-dimensional
enclosures, modeled through the streamfunction-only formulation of the flow equations under the
Boussinesq approximation and the associated energy equation. The transient version of this classical
coupled heat and fluid flow problem was solved through integral transformation, and compared
against previously reported numerical solutions. We consider a square air-filled enclosure, with
differentially heated lateral walls, and insulated top and bottom walls. Buoyancy effects are taken
into account through the Boussinesq approximation, under laminar flow regime. The transient
behavior of the coupled heat and fluid flow phenomena was investigated, for different values of the
Rayleigh number, Ra.
PATTERNS OF BIFURCATING CONVECTIVE FLOWS IN LONG HORIZONTAL CAVITIES
Alexander Yu. Gelfgat, Pinhas Z. Bar-Yoseph, and Alexander L. Yarin
Computational Mechanics Laboratory, Faculty of Mechanical Engineering,
Technion - Israel Institute of Technology, Haifa 32000, Israel
Fax. 972-4-829324533,
e-mail: merbygr@cmlp.technion.ac.il
A bifurcation from steady to oscillatory state of buoyant convective flow in laterally heated
rectangular cavities is numerically investigated. The considered flow is defined by the momentum,
the continuity and the energy equations in the Boussinesq approximation and the three characteristic
parameters: Grashof number Gr, Prandtl number Pr and the aspect ratio of the cavity (length/height)
A. Cavities with 4 no-slip boundaries, isothermal vertical boundaries and perfectly insulated
horizontal boundaries are considered. Case of a stress-free upper boundary was considered in 1. The
analysis is focused on the case of low Prandtl number fluid, in particular Pr = 0 and Pr = 0.015. The
aspect ratio is varied from 1 to 10.
The problem was numerically investigated using the spectral Galerkin method with globally defined
basis functions which satisfy all the boundary conditions and the continuity equation. The global
formulation of the Galerkin method allows us to decrease the number of degrees of freedom (number
of scalar modes in the numerical method), which gives a possibility to investigate consequently
steady states, their stability and weakly supercritical states of the flow in the framework of a single
model. Results of Galerkin method are verified by solution of the full unsteady Boussinesq problem
with the use of the finite volume method. Both numerical techniques are described in detail in 2,3.
The most unexpected result of this study is existence of several branches of steady states. For aspect
ratio 4 the existence of 2 different steady states was previously reported 4, namely flow with one
main convective vortex and flow with 2 separated vortices. While stability of these known states was
studied, other branches steady states flows with 3 and 4 separated vortices were discovered for
cavities of larger aspect ratios. Examples of such flows are shown in Figs. 1 and 2. These steady
states were calculated first by the Galerkin method and then some of them were reobtained by the
finite volume method which approved their existence. Another set of multiple steady states was
found for cavities with 1 < A < 2 and Pr = 0 (Fig.3). Initially all the steady flow are symmetric with
respect to rotation around the center of the cavity. Lower line between points A and B in Fig.3
corresponds to a steady bifurcation from symmetric to non-symmetric steady state (Fig.4). Upper
line between points I and II corresponds to the oscillatory instability of non-symmetric steady states.
Region in Gr-A plane where non-symmetric steady states are stable becomes smaller with the
increase of the Prandtl number and completely disappears at Pr = 0.015.
Other objectives of this study are to compare oscillatory instability at zero and low Prandtl numbers
(Pr = 0.015) and at large and infinite aspect ratios (A = 10 and the infinite fluid layer, A = ¥). It was
found that a similarity between the most unstable perturbations at Pr = 0 and 0.015 as a rule does
not exist. Such similarity may be found, for example, at A = 4 (see Ref.2) for single-vortex steady
states. Behavior of steady states at large aspect ratios show some analogies with the infinite layer.
Namely, a single-vortex state transforms into a many vortex state and vice versa. These transitions,
depending on the aspect ratio and the Prandtl number, may either continuously transform one into
another or change abruptly because of instability of one of them. On the other hand, no asymptotic
behavior for large A was found for the critical Grashof number and the critical frequency
corresponding to the onset of oscillatory instability. The most unsteady perturbations also show that
the influence of the confined geometry on the stability of the flow cannot be neglected. This is
illustrated in Fig.5 where isolines of the flow at the critical values of parameters are shown together
with isolines of the most unstable perturbation of this flow. It is seen that at A =10 the flow has
spatially periodic features, as it is expected by the analogy of an infinite fluid layer. On the other
hand, the most unstable perturbation has no such features which means that the confined shape of the
cavity has an important influence on the onset of the instability.


ACKNOWLEDGEMENT
This research was supported by the German-Israeli Foundation for Scientific Research and
Development, grant No.I-284.046,10/93.
REFERENCES
- Gelfgat A.Yu., Bar-Yoseph P.Z. and Yarin A.L. Numerical Investigation of Hopf Bifurcation Corresponding to Transition From Steady to Oscillatory State in a Confined Convective Flow. Proc. of the 1996 ASME Fluids Ercgiheering Division Summer Meeting, FED - vol.237, pp 369-374,1996.
- Gelfgat A.Yu. and Tanasawa I. Numerical Analysis of Oscillatory Instability of Buoyancy Convection with the Galerkin Spectral Method. Numerical Heat Transfer. Part A., Vol. 25, pp 627-648,1994.
- Gelfgat A.Yu., Bar-Yoseph P.Z. and Solan A. . Stability of Confined Swirling Flow with and without Vortex Breakdown. Journal of Fluid Mechanics, Vol. 31 l, pp 1-36,1996.
- Roux B. (ed.). Numerical Simulation of Oscillatory Convection in Low-Pr Fluids: A GAMM Workshop. Notes on Numerical Fluid Mechanics, Vol. 27,1989.
NUMERICAL DETERMINATION OF THE CORRELATIONS QUALIFYING THE MASS AND HEAT TRANSFER AROUND A SPHERE SATURATED WITH A PURE LIQUID IN NATURAL CONVECTION
M. BOUAZIZ, A. DAÏF*, A. ALI CHERIF, X. CHESNEAU
Laboratoire de Mécanique, Acoustique et Instrumentation, UPRES EA 1945
Université de Perpignan, 52, Avenue de Villeneuve 66860 PERPIGNAN France
ABSTRACT
The work that we present concerns the determination of correlations expressing mass and heat transfers around a sphere in natural convection.
Various authors have undertaken theoretical and experimental work on the determination of expressions that give average Nusselt and Sherwood numbers. Renksizbulut and Yuen1 have studied the mass and heat transfer around a sphere saturated with liquid evaporating in forced convection. Yuge2, Amoto and Tien3 have experimentally studied the heat transfer in natural convection around a sphere. Ranz and Marshall4 have proposed expressions of Nusselt and Sherwood numbers in natural convection, these last have been obtained by analogy with the data proposed by Frössling5 in pure forced convection.
In this study, we are interested in heat and mass transfers around a sphere in a gas environment. The sphere is porous and saturated with a single constituent liquid. The study is envisaged in natural convection by taking into account the variation of physical properties according to the temperature and pressure. To describe the liquid-vapor equilibrium and to determine the molar fraction at the surface of the sphere in a high pressure gas we use the fugacity and the Redlich-Kwong equation. In addition, equations of mass and heat transfers are linked, due to the fact of taking into account the enthalpic diffusion in the heat equation.
The resolution of transfer equations (impulsion, heat and mass) around the sphere allows us to determine local Nusselt and Sherwood numbers. The knowledge of the values of these numbers is exploited to define their average values by integration. A dimensionless equation allows us to give a more general form of the equations and to show thermal and mass Grashof numbers. Equations and boundary conditions are obtained by the utilization of the finite difference implicit method. The sampling step following is constant ; following y, a preliminary study is realized to determine a convenient scale. The different stages followed up for the resolution of the equations are :
- Initialization of the calculation by taking temperature, speed and concentration profiles (calculation point near from the stagnation point).
- Resolution of the mass transfer equation.
- Resolution of the heat transfer equation.
- Resolution of the movement equation.
- Test of the thickness of the hydrodynamic layer limits : if the test is positive one passes to the next stage, otherwise, one increases the thickness and one returns to stage 2.
- Passage to the next section.
- End of calculations for an angle = 170°.
We have undertaken the calculation for different liquids (decane, octane, hexane, ethanol, methanol and water) with a molar mass varying from 18 to 142 g/mol. The temperature and the pressure of the gas vary respectively from 300 to 673 K and 1 to 60 bar. To take into account the mass and thermal natural convection in the Nusselt and Sherwood numbers' expressions, we have determined an average Grashof number with the thermal and mass Grashof number. To give a general character to the expressions, we have used a large number of calculation points.
The adopted form of the expressions that we seek to determine as functions of heat (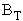 ) and mass ( ) and mass ( ) transfer numbers as well as Prandtl (Pr) and Scmidt (Sc) numbers is as follows : ) transfer numbers as well as Prandtl (Pr) and Scmidt (Sc) numbers is as follows :
 (1) (1)
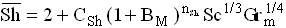 (2) (2)
A first determination of the coefficients  gives different values according to the products and the pressure studied. To find a valid expression for all products and for all pressures, one determines expressions of gives different values according to the products and the pressure studied. To find a valid expression for all products and for all pressures, one determines expressions of  according to the mass expansion coefficient of the fluid ( according to the mass expansion coefficient of the fluid ( = = ) and to the pressure and to ) and to the pressure and to  according to the pressure. The results of this analysis are represented in figures 1 and 2 and allow us to obtain expressions of Nusselt and Sherwood numbers. according to the pressure. The results of this analysis are represented in figures 1 and 2 and allow us to obtain expressions of Nusselt and Sherwood numbers.
REFERENCES
- Renksizbulut, M. and Yuen, M.C., "Numerical study of droplet evaporation in a high-temperature stream" Journal of Heat Transfer,Vol 105, pp 389-397, May, 1983.
- Yuge, T., "Experiments on heat transfer from spheres including naturel and forced convection", J. Heat transfer, N°3, 82, 1960.
- Amato, W. S. and Tien, C., "Free convection heat transfer from isothermal spheres in water", Int. J. Heat and Mass Transfer, Vol. 15, pp 327-339, 1972.
- Ranz, W.E. and Marshall, W.R., "Evaporation from drops", Chemical Engineering Progress Vol 48, No 3, pp 141-146, March, 1952.
- Frössling, N., "Ûber die verdûugtug fattender tropfen gerlands beitrôge fûr geophysik", 52, pp 170-215, 1938.
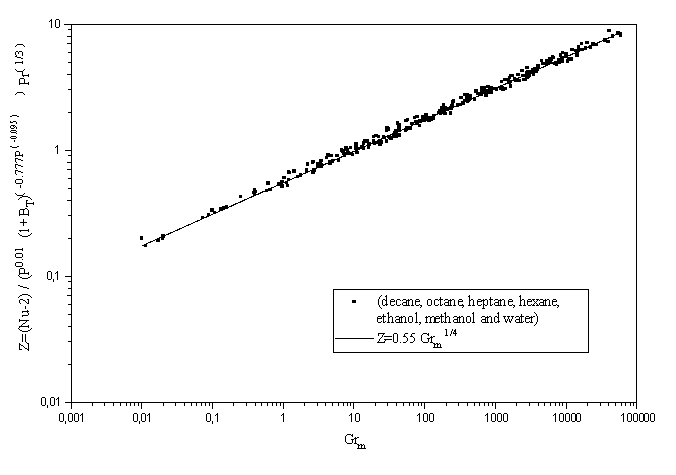
Figure 1 : Nusselt number evolution according to the average Grashof number
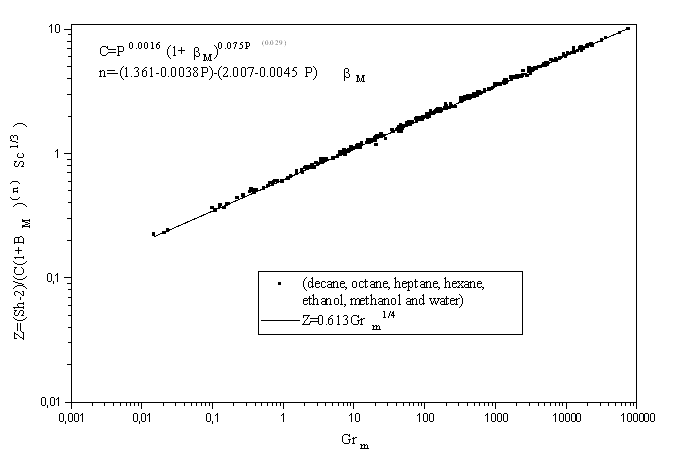
Figure 2 : Sherwood number evolution according to the average Grashof number
TRANSIENT NATURAL CONVECTION IN AN ENCLOSURE FILLED WITH A SATURATED POROUS MEDIUM
A. A. Merrikh, I. Pop* and A. A. Mohamad
Mechanical Engineering Department, Eastern Mediterranean University,
G.Magosa, N.Cyprus via Mersin10-Turkey
* Faculty of Mathematics,
The University of Cluj, R-3400 Cluj, CP 253, Romania
ABSTRACT
Transient convective flow in an enclosure filled with a saturated porous medium is investigated using Darcy-Boussinesq approximation. The flow inside a rectangular enclosure filled with a saturated porous medium is driven naturally due to the temperature difference between the vertical walls of the enclosure where the horizontal walls are assumed adiabatic. A second order accurate in time and in space, MacCormack scheme is used for the numerical solution of the time dependent energy equation. The present analysis is performed for Rayleigh numbers in the range of 1-1000 and aspect ratio 0.5-2. Grid and time step independence is carefully tested and flow structure and heat transfer characteristics are presented for the above ranges of parameters. A slow recirculated flow starts next to the hot vertical wall of the enclosure. It is observed that there is a certain time needed for the flow to penetrate towards the cold side wall. This time period was found to be dependent on aspect ratio and Rayleigh number. It was also observed that as aspect ratio increases, the time to achieve steady state increases and rate of heat transfer decreases.
Model Equations
Two dimensional, incompressible, Darcy-Boussinesq approximated fluid flow and heat transfer is modeled using following set of nondimensional equations. Heat transfer is modeled assuming local thermal equilibrium between the porous matrix and the fluid. Governing equations are:
 (1) (1)
 (2) (2)
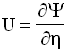  (3) (3)
Boundary Conditions
The stream function and velocity components normal to solid (impermeable) walls are set to zero. The horizontal walls of the cavity are adiabatic i.e., the temperature gradient at the horizontal walls is set to zero while one vertical side wall is kept at high temperature.
Adiabatic horizontal walls:   (5) (5)
Isothermal vertical walls: 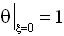  (7) (7)
Method of Solution
The above equations (1-2) together with the boundary conditions are solved numerically. The stream function (Poisson equation) is solved by finite difference. Energy equation is advanced in time by using MacCormack scheme [1]. In order to obtain grid and time independent results, several grid and time steps are tested. It was obtained that 121x121 grid points with 5x10-6 time step would achieve a grid and time independent solution.
Results and discussion
As the vertical wall of the enclosure is suddenly heated, the fluid particles at the neighborhood of the wall receive heat and their density decreases causing the lighter fluid to rise vertically being replaced by the cold fluid particles, Fig-1. This makes a recirculation and as time proceeds, the fluid particles become hotter and penetrate towards the core of the cavity, i.e., stretching the recirculation. The flow penetrates towards the cold vertical wall and then reaches steady state. As Rayleigh number increases, the time for the flow to reach steady state decreases. It was also observed that increasing aspect ratio decreases the rate of heat transfer from the hot vertical wall, Fig-2.
Conclusion
Transient convective flow in an enclosure filled with a saturated porous medium is investigated numerically. It was observed that there is a certain time needed for the flow to reach the cold side wall and this time period was found to be dependent on aspect ratio and Rayleigh number. It was also observed that as aspect ratio increases, the time to achieve steady state increases and rate of heat transfer decreases.
References
- A. Merrikh, Transient Natural Convection in Open Cavities, M.S.M.E. Thesis, Eastern Mediterranean University, 1996.

THE PENETRATION OF UNSTEADY FREE CONVECTION FROM A HEATED AND COOLED VERTICAL FLAT SURFACE IN A POROUS MEDIUM
R. BRADEAN and D. B. INGHAM
Department of Applied Mathematical Studies
The University of Leeds, Leeds, LS2 9JT, England
P. J. HEGGS
Department of Chemical Engineering
UMIST, Manchester, M60 lQD, England
I. POP
Faculty of Mathematics, The University of Cluj
R-3400 Cluj, CP 253, Romania
ABSTRACT. Unsteady two-dimensional free convection is generated by an impulsively heated
and cooled, in space, infinite vertical flat surface which is embedded in a stationary
porous medium. The matched asymptotic expansions technique is used to obtain approximate
analytical solutions for small values of time and these results are found to be in very
good agreement with the finite-difference results for all the values of the Rayleigh
number considered, namely 0 < Ra < 100. It is found that the flow consists of a row of
counter rotating cells, each cell developing along the hot or cold regions of the surface.
For values of Ra larger than about 40, and for small times, two recirculating regions
develop at the point of collision of the two opposite streams which flow along the
surface. At large values of time the unsteady numerical solution converge to the steady
state results.
NUMERICAL SOLUTIONS FOR BUOYANCY-DRIVEN FLOW IN A 2-D SQUARE ENCLOSURE HEATED FROM ONE SIDE AND COOLED FROM ABOVE
Orhan AYDIN, Ahmet UNAL ve Teoman AYHAN
Karadeniz Technical University, 61080 Trabzon, TURKEY
ABSTRACT
Buoyancy-driven flows in fluid-filled enclosures have received considerable attention in recent years. Attention is justified by its many applications including heating and cooling of building spaces, solar collectors, cooling of electronic equipment, thermal energy storage, convection in lakes, crystal growth in liquids, etc. The determination of buoyancy-driven flow in enclosures also provides a comparison of numerical methods dealing with viscous flow calculations. Numerous studies exist in the literature related to investigating natural convection in enclosures. A recent review of existing literature is given by Ostrach1. Most of the previous researches have addressed natural convection in enclosures due either to a horizontally or vertically imposed temperature difference. Rather little work has been carried out on flows regarding more complex boundary conditions. However, very different boundary conditions are present in practice. For example, in cooled ceiling systems in buildings, the heat gained from the side is withdrawn by cooled ceiling2.
In this study, steady natural convection in a two-dimensional square enclosure isothermally heated from one side and isothermally cooled from above is numerically investigated. The other side and bottom are perfectly insulated. Air with a Prandtl number of 0.71 is used as a working fluid. The usual stream function and vorticity aproximation is used through the Bousinesq approximation. The governing equations are solved numerically, employing finite-difference methods. The vorticity-transport and energy equations are solved by the Alternating Direction Implicit (ADI) method of Peaceman and Rachford, the stream function equation being solved by SOR. The discretized transient equations are marched in time to an asymptotic steady-state solution. Hybrid-differencing is employed for the convective terms for numerical stability because higher values of Grashof numbers are considered. The diffusive terms and the buoyancy term are discretized by central differencing. Iteration convergence is obtained for stream function at each time step.
In order to test and validate the computer code developed in the present study, a buoyancy-driven flow in a square cavity which has differentially heated vertical walls and adiabatic upper and bottom walls is studied. This configuration has been considered by many researchers. The results obtained for this configuration in this study are compared with those given in an earlier study by de Vahl Davis3, which serves as a benchmark for comparison in many studies on natural convection.
In the present study, the values of Prandtl number between 0.01 and 100 are considered in order to investigate the influence of the Prandtl number. The computations are caried out for Rayleigh numbers ranging from 102 to 109. The results are presented in the form of streamlines and isotherms. Based on computations, average Nusselt number for heated vertical wall is calculated and the the highest Rayleigh number at which steady state laminar flows are possible is determined for each Prandtl number under consideration.
REFERENCES
- Ostrach, S., Natural Convection in Enclosures, J. Heat Transfer, 110, 1175-1190, 1988.
- Niu, J. and van der Kooi, J., Indoor Climate in Rooms with Cooled Ceiling Systems, Building and Environment, 29, 283-290, 1994.
- de Vahl Davis, G., and Jones, I.P., Natural Convection in a Square Cavity, a Comparison Exercise, Int. J. Num. Meth. Fluids, 13, 227-248, 1983.
MOLECULAR DYNAMICS SIMULATION ON VAPOR SHIELDING UNDER HIGH HEAT LOAD
S.Toda, H.Nakadate, H.Hashizume and Y.Katsumura
Department of Quantum Science and Energy Engineering,
Tohoku University, Aramaki, Aoba, Sendai, 980-77, Japan
Tel: +81 22 217 7901 Fax:+81 22 217 7904
E-mail: stoda@hll.nucle.tohoku.ac.jp
ABSTRACT
Introduction
In tokamak device, a plasma disruption leads to high energy deposition on portions of the first wall or divertor plate for short time. Therefore it becomes important to evaluate erosion thickness for the purpose of estimating lifetimes of divertor plate and first wall armor materials. However, an incident high heat flux on a surface of the divertor plate can produce ablated vapor cloud, and it reduces the total energy transported to the ablating surface. In order to numerically analyze the process of this vapor shielding, a heat conduction problem with phase change has to be solved together with Boltzmann equation, ionization balance, radiation transport equation and so on. Although several models for the vapor shielding have been developed for years, the physics of such a process is too complex to perform numerical analysis. In this study, we adopt the molecular dynamics method to analyze the effect of the vapor shielding.
Calculating method
In molecular dynamics method, the equations of motion for a collection of particles in a simulated cell are numerically calculated with short time interval. Several properties can be calculated with using obtained data for position and velocity of all particles at each time step.
In this study, the Lennard-Jones potential function is used to determine the interaction of molecules. Melting and evaporation processes of an argon wall in a call are simulated with incident helium particles. The periodic boundary condition is assumed on four surfaces of the simulated cell, and the other two surfaces is taken as a constant temperature surface and a plasma incident surface, respectively as shown in Figure 1.

Figure 1. A schematic diagram of a simulating cell.
Result
Behaviors of the particles are simulated about for 0.2 nsec with 2.0 fsec time interval. Figure 2 shows some snapshots of the calculation cell of simulation. The argon wall melts and evaporation occur.
Transition of the average kinetic energy of the incident helium particles near above the argon wall is shown in Figure 3. With the development of vapor layer, the energies of incident helium particles decrease because of elastic collisions with vapor atoms, which can be regarded as formation of the vapor shielding. The effect of the shielding is estimated about 40% in this case.
Conclusion
In this study, the process of melting and evaporation of the solid argon wall was simulated with using molecular dynamics method. The vapor shielding effect with elastic collisions occurred in this system and the erosion ratio is decrease with the growth of the vapor layer. In order to analize highly non-equilibrium processes such as a disruption ablation, the molecular dynamics is a effective simulating method.

Figure 2. Some snapshot of the calculating cell. Black points and null circles indicate the incident helium and argon atom, respectively.
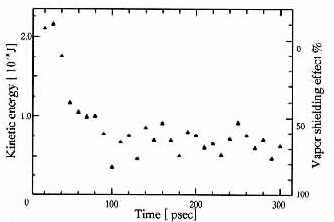
Figure 3. Transition of average kinetic energy of incident helium atoms and effect of the vapor shielding.
EFFECTIVE THERMAL CONDUCTIVITY OF TWO-DIMENSIONAL POROUS MEDIA
Fernando Manuel Ramos
e-mail: fernando@lac.inpe.br
Instituto Nacional de Pesquisas Espaciais (INPE)
Laboratório Associado de Computação e Matemática Aplicada (LAC)
Caixa Postal 515
12201-970 - São José dos Campos - SP - Brazil
The determination of the effective thermal conductivity of porous media is a problem of great interest to engineers and geophysicists. Particularly, this is an important issue in the development, for space applications, of two-phase thermal control systems, such as heat pipes and capillary pumping loops (CPL). Denoted by k e, the effective thermal conductivity is defined as the conductivity of an equivalent homogeneous medium which exhibits the same steady-state characteristics as the heterogeneous body. The value of k e is minimum if the different media are disposed in layers normal to the direction of heat flow. On the other hand, the maximum value is attained when all materials are arranged in parallel to the heat flux. Two recent studies reveal the existence of several empirical correlations and theoretical models1-2.
The goal of this article is to present a simple and versatile methodology for the solution of the diffusion equation in two-dimensional heterogeneous bodies. The present approach, based on an explicit finite-difference scheme, handles any geometry which can be represented on a rectangular grid. Although we restrict our focus to two-dimensional bodies made up of one or two materials, the method of solution is general and can be extended to three-dimensional heterogeneous solids composed of several media.
The problem is governed by the diffusion equation in a two-dimensional domain composed of one or two isotropic and homogeneous media, subjected to an initial condition and to boundary conditions of second or third kind. Across the interfaces of different materials, there is continuity of temperature and heat flux. The thermophysical properties are assumed to be temperature-independent. An uniform square Cartesian mesh is used to discretize the computational domain.
To illustrate the proposed methodology, two representative examples are considered. The first example concerns the problem of determining the effective thermal conductivity of a two-dimensional array of touching square cylinders, as shown in Fig. 1, representing a spatially periodic porous medium. Because of the symmetry of the thermal paths, a common approach in this case is to estimate the average properties from the thermal behavior of a unit cell, assuming adiabatic conditions at the local boundaries parallel to the macroscopic heat flux. The results, computed for a wide range of conductivity ratios, are found to be in excellent agreement with experimental and numerical data of Nozad et al.3 and Hsu et al.1 .

Figure 1: Array of touching square cylinders and its corresponding unit cell (dotted square).
In the second example, we consider the problem of determining the effective thermal conductivity of a Sierpinski carpet (SC), constructed according to the procedure depicted in Fig. 2. At order n = 1, the initial filled square is devided into nine equal-sized smaller pieces, the central square being removed. At subsequent orders, this procedure is repeatedly applied to the remaining squares. The effective thermal conductivity of a SC was computed up to the forth construction stage. The results are found to be in accordance with Archie's law, relating k e and porosity in rocks fully saturated by a conducting fluid4 ,. and results are also in good agreement with those obtained by Thovert and collaborators5.

Figure 2: Construction of the Sierpinski carpet.
REFERENCES:
- Hsu, C.T., Cheng, P., and Wong, K.W. "A Lumped-Parameter Model for Stagnant Thermal Conductivity of Spatially Periodic Porous Media", ASME Journal of Heat Transfer, Vol. 117, pp.; 265-269, 1995.
- Tavman, I.H. "Effective Thermal Conductivity of Granular Porous Materials", International Communications in Heat and Mass Transfer, Vol. 23, Nº 2, pp. 169-176, 1996.
- Nozad, I., Carbonnel, R.G., and Whitaker, S. "Heat Conduction in Multiphase Systems, Theory and Experiment for Two-Phase Systems, Chemical Engineering Science, Vol. 40, pp. 843-855, 1985.
- Nigmatullin, R.R., Dissado, L.A., and Soutougin, N.N. "A Fractal Pore Model for Archie's Law in Sedimentary Rocks", Journal of Physics D: Applied Physics, Vol. 25, pp. 32-37, 1992.
- Thovert, J.F., Wary, F., and Adler, P.M., 1990, "Thermal Conductivity of Random Media and Regular Fractals", Journal of Applied Physics, Vol. 68, pp. 3872-3883.
|

