|
Session 10
NATURAL CONVECTION II
Chairman: D. Pepper
SPECTRAL FINITE DIFFERENCE ANALYSIS OF NATURAL CONVECTION FROM ROWS OF VERTICAL FINS
Yoshihiro MOCHIMARU * and Chang-Yu LIU **
*Dept. of International Development Engineering
Tokyo Institute of Technology, Tokyo 152, Japan
**School of Mechanical & Production Engineering
Nanyang Technological University, Singapore
INTRODUCTION
Natural convection heat transfer from a fin array is one of the major concerns on cooling of integrated circuits & electronic devices. Many analytical or experimental studies have been reported. This paper presents an analytical study on natural convection from a vertical fin array using a spectral finite difference method. Both the flow & the temperature fields are presented.
ANALYSIS
It is assumed that the fin array is mounted vertically & the temperature on the base is constant & uniform. It is also assumed that the height of the fin is small & the fin thermal efficiency is approximately unity. In this analysis, all the length are made dimensionless with respect to the gap c between the fins. Dimentionless temperature T is defined as  , where T' is the local temperature of the fluid, , where T' is the local temperature of the fluid,  : the ambient temperature, : the ambient temperature,  : the uniform temperature on the base plate. Reference velocity U is defined so that : the uniform temperature on the base plate. Reference velocity U is defined so that  ,where Gr : Grashof number based on ,where Gr : Grashof number based on  and c; and c;  : kinematic viscosity. Since the heat and fluid flow field is periodic in space, only one unit cell domain corresponding to the region enclosed by two fins is considered for numerical solution. Without loss of generality, it is assumed that the region extended to semi-infinite space is expressed in a Cartesian coordinate system by : kinematic viscosity. Since the heat and fluid flow field is periodic in space, only one unit cell domain corresponding to the region enclosed by two fins is considered for numerical solution. Without loss of generality, it is assumed that the region extended to semi-infinite space is expressed in a Cartesian coordinate system by  . .  corresponds to the base plate. Let the dimensionless height of the fins be L, so that fins are denoted by corresponds to the base plate. Let the dimensionless height of the fins be L, so that fins are denoted by  ,or ,or  Due to the symmetry of the heat and fluid flow field, Due to the symmetry of the heat and fluid flow field,  along the axes ( along the axes ( or or  ) which does not lead to steady-state fields of infinite extension with finite temperature. Instead, to get steady-state fields of semi-infinite extension, the following assumptions along the axes ) which does not lead to steady-state fields of infinite extension with finite temperature. Instead, to get steady-state fields of semi-infinite extension, the following assumptions along the axes 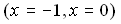 are introduced : are introduced :   , , where where  is a suitable constant to be given a priori. Using the following coordinate system ( one of a conformal mapping system ) is a suitable constant to be given a priori. Using the following coordinate system ( one of a conformal mapping system )   , ,

or equivalently

The equation of vorticity transport under Boussinesq approximation, the relation between vorticity and the stream function, and the energy equation neglecting dissipation can be given by ( in dimensionless forms )
 (1) (1)
 (2) (2)
   (3) (3)
  (4) (4)
where  , and Pr denote a dimensionless stream function, dimensionless vorticity, and a Prandtl number respectively. The boundary of the domain is expressed by , and Pr denote a dimensionless stream function, dimensionless vorticity, and a Prandtl number respectively. The boundary of the domain is expressed by 
BOUNDARY CONDITIONS
Boundary conditions are
 or or  or or 

 or or 
 or or 
 or or  or or 
 or or 
 or or 
NUMERICAL SOLUTION PROCEDURE
Since the analyzed region is expressed by  the independent variable the independent variable  can be transformed in such a way that can be transformed in such a way that  . Thus the coordinate system . Thus the coordinate system  can be replaced by can be replaced by  A spectral finite difference scheme A spectral finite difference scheme by a time marching method is applied. For a symmetrical solution the following form is assumed: by a time marching method is applied. For a symmetrical solution the following form is assumed:
 , ,  (5) (5)
To maintain numerical stability for getting a steady-state solution by a semi-implicit scheme independently of each component at a stage of time integration, terms    are added to the left hand side of Eqs.(1),(2), and (3) respectively, where are added to the left hand side of Eqs.(1),(2), and (3) respectively, where  is a time increment for integration; is a time increment for integration;  is a suitably chosen constant. Treatment for mixed boundary conditions ( Dirichlet and Neumann conditions ) is the same as in Ref.2. Auxiliary conditions at is a suitably chosen constant. Treatment for mixed boundary conditions ( Dirichlet and Neumann conditions ) is the same as in Ref.2. Auxiliary conditions at  are given by are given by     As an initial condition for numerical integration, the following are used: As an initial condition for numerical integration, the following are used:  ( inside the domain ). Time integration is based on a semi-implicit scheme. ( inside the domain ). Time integration is based on a semi-implicit scheme.
NUMERICAL RESULTS
Steady-state mean Nusselt number  over the fin and base plate surfaces is given by over the fin and base plate surfaces is given by
 (6) (6)
where  Steady-state streamlines and isotherms for air are shown in Figs.1 - 6 under three conditions. Figure 7 shows variation of mean Nusselt number Steady-state streamlines and isotherms for air are shown in Figs.1 - 6 under three conditions. Figure 7 shows variation of mean Nusselt number  against against  for air. for air.

CONCLUSION
It was demonstrated that, with proper transformation of governing equations and boundary conditions, it is possible to solve the natural convection heat transfer from a fin array, using a spectral finite difference method. Both the flow and temperature fields were presented in terms of various parameters.
REFERENCES
- Y.Mochimaru, A Spectral Finite Difference Scheme and its Effectiveness, Proc. 26th Ann. Iranian Math. Conf., Vol.2, 245-254(1995).
- Y.Mochimaru, Extension of Applicability of a Spectral Finite Difference Scheme to Mixed
 Boundary Conditions, 9th International Sym. Transport Phenomena in Thermal-Fluids Engineering, Vol.1, 315-320(1996). Boundary Conditions, 9th International Sym. Transport Phenomena in Thermal-Fluids Engineering, Vol.1, 315-320(1996).
NUMERICAL INVESTIGATION OF LAMINAR NATURAL CONVECTION IN A FOIL TYPE TRANSFORMER
Dr. J. Declercq*, N. Erkens**, Prof. Dr. E. Van den Bulck**
*Pauwels Trafo N.V. , Antwerpsesteenweg 167, 2800 Mechelen, Belgium
Tel. (32)15 283351 Fax. (32) 15 283216 Email. Jan_Declercq@compuserve.com
**K.U.Leuven, Dept. of Mechanical Engineering, Celestijnenlaan 300A, 3001 Heverlee, Belgium
Email. Nancy.Erkens@mech.kuleuven.ac.be , Erik.Vandenbulck@mech.kuleuven.ac.be
INTRODUCTION
The main factor limiting transformer life is the hottest spot temperature inside the windings. According to the Montsinger relation, life expectancy of the electric insulation around those windings is halved for every 6 K temperature rise. This makes accurate prediction of the temperature distribution inside the transformer and particularly of the hottest spot temperature essential.
Since in operating conditions only the top oil temperature is measured, correlations are needed to calculate the temperatures in the windings. The available Nusselt correlations in literature involve 2D natural convection between vertical plates, subjected to either symmetric, uniform heat flux or uniform wall temperature as can be seen in Figure 1. These simplified boundary conditions hardly correspond with the real life problem, where asymmetric, highly non-uniform heating rates are present.
This study conducts a CFD-calculation of the hot spot temperatures for the parallel plate geometry, with highly non-uniform heating and mineral oil as the working fluid. After experimental verification of the CFD-model, it compares the obtained Nusselt number with Nusselt numbers, calculated from available correlations in literature.
The application of these results lies in the power transformer industry, where better predictive models of heat transfer are needed. This study has been dedicated to foil type winding of a 25 MVA transformer, restricted to one channel. The foil type winding consists mainly of copper or aluminium foil, covered with insulation and wound cylindrically, with radial cooling channels in between. The non-uniform heat production is caused by the electric current passing through the foil and supplementary losses near top and bottom of the windings due to stray losses.
  
Figure 1. Terminology Figure 2. CFD-calculated temperature field
GOVERNING EQUATIONS
The problem considered is a 2D conjugate heat transfer problem. The laminar flow of the incompressible fluid is governed by the continuity equation and the Navier-Stokes equations extended with a buoyancy source term.
 (1) (1)  (2) (2)
Since heat transport is involved, an additional transport equation has to be solved to compute the temperature. Temperature dependence of cooling mineral oil has to be taken into account.
BOUNDARY CONDITIONS
The inlet temperature was held constant at 52.1 °C. The pressure drop of 17 Pa in the cooling unit (not modelled here) was imposed as a counter pressure at the outlet. The heat losses, due to the electric current through the foil and supplementary losses at top and bottom, were imposed as a volumetric heat generation. The heat generation is highly non-uniform and exceeds the average heat flux with 30 % at the bottom and the top of the foil.
NUMERICAL ASPECTS
The model was implemented in the PHOENICS code, using a staggered grid arrangement. The 2D simplest algorithm was used. The hybrid difference scheme was applied. Convergence was reached at 800 sweeps, using conservation of mass and energy as convergence criterion.
A profound grid study pointed out that a minimum of 35 exponentially distributed cells have to cover the width of each cooling channel, to reach grid independent results.
A linear relaxation factor of 0.2 was used for pressure and 0.6 for temperature. For the vertical velocity a false time relaxation of 0.001 was used. Pressure and temperature were solved by the whole-field method, velocity was solved point-by-point.
EXPERIMENTAL MEASUREMENTS
Pauwels Trafo performed temperature measurements inside the windings at the presumed hot spots on a full scale transformer. To do so, Copper-Constantane thermocouples with a thin epoxy insulating layer were wound together with the foil. They were located at 9 mm from the top of the foil and mid-width of each bundle. Temperature measurements were started after nineteen hours of operation, to ensure stabilised temperatures.
CFD-CALCULATED NUSSELT NUMBER AND TEMPERATURES
Figure 2 shows the temperature field in the foil windings and the cooling channels. Cold fluid entering at the bottom is heated by the heat, released in the windings. Figure 3 presents the computed Nusselt number in one of the cooling channels. The higher Nusselt number at the entrance is due to entrance effects. In the middle section the Nusselt number is quite constant. Near the exit region the Nusselt number increases again, because of the exponential increase in the heat, released in the windings near the top. The mean discrepancy derived from the measured temperatures versus the CFD-calculated temperatures for each of the foil bundles is 2.5ºC.
 
Figure 3. CFD computed Nusselt number Figure 4. Comparison of CFD-calculated wall versus height temperature with wall temperatures calculated
from correlations in literature
Figure 4 presents the CFD-calculated wall temperatures over the full height of the foil both for uniform and non-uniform volumetric heat production. Hot spot temperatures for non-uniform heat production are up to 30% higher than for uniform heat production.
Figure 4 also shows the wall temperatures at height x=L, as predicted by several correlations, found in literature. Those correlations all largely underestimate the corresponding CFD-calculated wall temperature at that height. This urges for new correlations which should show a spatial dependency factor including entrance effects and non-uniform heat flux distributions. Research is now directed towards CFD based computations.
CONCLUSIONS
Comparison of the CFD-calculated wall temperatures at the top of the foil with those calculated from correlations in literature, clearly shows that available correlations in literature cannot accurately predict hot spot temperatures. Even the best fitted correlation gives an underestimation of the hot spot temperature by 20% for a uniform heat input and by 40% for a non-uniform heat input. Therefore, at this instance, CFD calculations are needed to accurately predict hot spot temperatures. Also, while available correlations in literature only allow to calculate wall temperature at a certain height, CFD renders much more elaborate information, like a full height temperature profile.
In further investigations, improved Nusselt correlations will be derived taking into account the non-uniformity of the heat flux, so that wall temperatures can be predicted more accurately over the full height of the foil.
REFERENCES
- Bar-Cohen, A., and Rohsenow, W. M., “Thermally Optimum Spacing of Vertical, Natural Convection Cooled, Parallel Plates”, ASME Journal of Heat Transfer, Vol. 106, p 116-123, 1984.
- Wirtz, R. A., Stutzman, R. J., “Experiments on Free Convection Between Plates With Symmetric Heating”, ASME Journal of Heat Transfer, Vol. 104, p 501-507, 1982.
- Churchill, S. W., Usagi, R., “A General Expression for the Correlation of Rates of Heat Transfer and Other Phenomena”, Journal of American Institute of Chemical Engineers, Vol. 18, p 1121-1138, 1972.
- Barrow, H., Prasad A.,Sherwin K., “Heat Transfer by Free Convection in Open Ended Vertical Ducts”, Natural Convection, p 59-63.
FLOWR, A ONE-DIMENSIONAL, TRANSIENT INTERFACIAL AREA MODEL: DESCRIPTION AND PRELIMINARY ASSESSMENT
N.U. Aydemir
Atomic Energy of Canada Limited
Safety Thermalhydraulics Branch
Whiteshell Laboratories
Pinawa, Manitoba
Canada R0E 1L0
SUMMARY
This paper presents an overview of the methodology and assumptions of the transient interfacial area model FLOWR. The paper also describes the implementation and testing of FLOWR in a prototype version of CATHENA 1 (Canadian Algorithm for THErmalhydraulic Network Analysis), a two-phase thermalhydraulic network code.
The evolution of interfacial area is modeled through the use of an interfacial area transport equation which is shown to be equivalent to a Boltzmann-type number density transport equation for bubbles (or droplets). The model is supplemented by additional constitutive laws that govern the average behavior of the gas-liquid interface. All quantities, including the interfacial area and number density functions are treated as continuous functions of time and space. This leads to a unique methodology in the treatment of coalescence and breakup phenomena. Since all the quantities defined are continuous, transitions between different flow regimes are smooth. In existing one-dimensional computer codes, flow regime transitions must be determined from flow regime maps and represented by interpolation of constitutive relations between the regions. In practice, the interfacial area is determined in a similar fashion, tied very closely to the flow regime maps. With the introduction of a smooth interfacial area function determined from a transport equation, the uncertainties associated with interpolation near flow regime transition regions are removed.
The transient interfacial area density model developed in the present work is integrated in a prototype version of the two-phase, two-fluid, thermalhydraulic systems code CATHENA. CATHENA has been in development at the Whiteshell Laboratories of AECL (Atomic Energy of Canada Limited) since the early 1980’s. It has extensively been validated against separate effects as well as integrated experiments. CATHENA is currently used in the safety and licensing analysis of AECL designed CANDU â (CANadian Deuterium Uranium) PHWRs (Pressurized Heavy Water Reactors). It is also used in the design, safety and licensing analysis of reactors for research and isotope production such as the IRF (Irradiation Research Facility) or MAPLE (Multipurpose Applied Physics Lattice Experimental).
Presently, CATHENA uses flow regime maps to determine the flow geometry and compute interfacial area density. This work describes an implementation of the proposed method for calculation of the interfacial area density in CATHENA and discusses its main features. However, it must be noted that, the flow regime itself is still determined from the CATHENA flow regime maps.
This paper also contains several validation cases for the adiabatic flow of air-water mixtures in horizontal and inclined pipes. The results obtained were physically sound and in close agreement with the experimental observations. Several examples of integral calculations (i.e., full facility simulations) are also given and compared with the results obtained using the current reference code version.
In practice, flow patterns are characterized by two-dimensional (2D) flow regime maps. The most common coordinates for 2D maps are liquid flow rate (either mass or volume flow rate) versus gas flow rate. The applicability of most of these maps is doubtful since they were based on experience with only a few fluids and usually under adiabatic conditions. The second part of the paper deals with relatively new concepts. The idea of a three-dimensional (3D) flow regime map is introduced for the first time and several maps are generated for vertical, inclined and horizontal pipes. A 3D flow regime map is obtained by plotting a flow regime indicator as the third variable against the superficial velocities (i.e. volumetric flow rates). The flow regime indicator is described in the paper. It must be noted that the range of validity of these maps is limited to bubbly flows.
Three-dimensional maps are believed to contain more information than their two-dimensional counterparts since the topology of a 3D map also reveals how a transition is approached from different directions. Examples of three dimensional maps are given for complex geometry such as a pipe with side branches. This is considered to be a significant contribution towards a better understanding of the flow regime evolution in manifolds (such as CANDU reactor headers). Unlike single pipes (vertical or horizontal), flow regime maps for manifolds with side branches cannot be generalized in the form of a 2D map because of different orientation and locations of side branches. It is believed that an examination of the 3D maps produced by the present model will enhance our current understanding of this very complex interfacial phenomenon.
The main conclusion of the paper is that calculation of interfacial area from a transport equation leads to a deterministic formulation, given that a suitable interfacial area advection velocity can be formulated. For bubbly or droplet flows, the natural choice seems to be the velocity of the discontinuous phase which is also adopted in the present model. For more complex formulations where clusters of bubbles or droplets are followed, different choices or models for the advection velocity may be required. Further research is needed to answer the question of suitability of one-dimensional models to represent phenomena that is truly multi-dimensional. For example, predicting flow regime transitions associated with instabilities of multi-dimensional nature is quite challenging. Calculation of interfacial area density from a Boltzmann-type transport equation is not new; what makes the present work unique is the level of detail at which various mechanisms are modeled. To the author’s knowledge, this is also the first time such a model is integrated in a large thermalhydraulic network code. However, the question of flow regime transitions has been left open. In the present work an attempt has been made in this direction by the introduction of flow regime indicators, however, this approach also needs further investigation.
Future work will extend the transition mechanisms considered and add to the pipe geometry and thermalhydraulic conditions that are of practical importance in pressurized water reactors.
Funding for the development of the Flow Regime Model was provided by the CANDU Owners Group agreement between AECL, Ontario Hydro, New Brunswick Power and Hydro Quebec.
REFERENCES
- Richards, D.J., Hanna, B.N., Hobson, N. and Ardron, K.H., A Two-Fluid Code for CANDU LOCA Analysis, Proceedings of Third International Meeting on Thermal Hydraulics, Vol.2, Newport, R.I., 1985.
|

