|
Session 17
UNSTEADY FLOW
Chairman: S. Güçeri
TRANSCILLATORY TRANSFER IN INTERACTING MULTI-COMPONENT SYSTEMS
Alexander Philippov, Muslim Minlibayev, Guzel Fatihova
Department of Physics
Sterlitamak State Pedagogical Institute, 453103, Sterlitamak, Russia
ABSTRACT. Earlier experiments have disclosed that during the oscillations in multi-component media the values of the coefficients of transfer increase (for example, the coefficient of heat conductivity in a porous medium). However, this paper proposes a new model for explaining this practically applicable physical phenomenon. The problem with mathematical formulations is that they lead to equations with periodic factors, which are impossible to analyze fully. Thus, we have investigated the main laws of transfer through computer modelling. A further benefit of the model is that, by expressing finite velocities of the expansion of disturbance, the deficiencies of incomprehensible variations inherent in the classical theory of heat conductivity and diffusion are removed.
On the basis of the model of a transcillator, it was possible to find analytical formulae for the calculation of the coefficients of transfer. It was thus possible to establish the conditions of the additivity of the coefficients of transfer. It was then necessary to establish the nature of the periodic oscillations in the dependence of the coefficients of transfer on oscillatory amplitude and frequency. The spectrum formulae for arbitrary oscillations of the medium were also found. Finally, there was a satisfactory correlation between the theory and the experimental evidence.
ON THERMOVIBRAITIONAL AND THERMOGRAVITATIONAL INSTABILITY OF PLANE HORIZONTAL FLUID LAYER UNDER FINITE VIBRATION FREQUENCIES
G. Z. Gershuni , I. O. Keller , I. O. Keller , B. L. Smorodin , B. L. Smorodin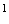
1 Perm State University, 614000, Perm, Russia,
2 Technion - Israel Institute of Technology, 32000-Haifa, Israel.
The consideration of the vibrational convective instability of a non-uniformly heated liquid in weightlessness for limiting case of the high frequencies vibration was based on the system of equations for averaged fields, which is received from Boussinesq equations of convection by means of the method of averaging1. Effect of vibration in the limit of high frequencies defines a single regime parameter - vibrational Rayleigh number  where where 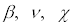 are coefficients of thermal expansion, kinematic viscosity and heat diffusivity, b and W are amplitude of displacement and angular frequency of vibration, Q is characteristic difference of temperatures, L is the characteristic linear size. The mechanical equilibrium (when it exists) becomes unstable when are coefficients of thermal expansion, kinematic viscosity and heat diffusivity, b and W are amplitude of displacement and angular frequency of vibration, Q is characteristic difference of temperatures, L is the characteristic linear size. The mechanical equilibrium (when it exists) becomes unstable when 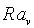 exceeds some critical values. The specific feature of high frequency approach is that we exclude the parametric excitation phenomena. exceeds some critical values. The specific feature of high frequency approach is that we exclude the parametric excitation phenomena.
Now the problem of the vibrational convective instability in the case of infinite plane horizontal layer of a liquid, limited by parallel rigid isothermal plates, in the presence of longitudinal vibration of finite (arbitrary) frequency is considered. In this case the frequency and amplitude of vibration are independent parameters. The basic solution can be written in the following form:
This is harmonic plane - parallel flow of the liquid.  is vibrational Rayleigh number; is vibrational Rayleigh number;  is a dimensionless frequency of vibration. This solution at limit case is a dimensionless frequency of vibration. This solution at limit case 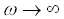 tends to "quasiequilibrium". In this case the most dangerous are plane disturbances. It is possible to show, that this property is valid at any frequencies. tends to "quasiequilibrium". In this case the most dangerous are plane disturbances. It is possible to show, that this property is valid at any frequencies.
For investigation of the stability of the basic solution we use small "normal" disturbances. The problem of linear instability of the basic condition for amplitudes of disturbances stream function  and temperature and temperature 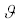 can be formulated in the following form: can be formulated in the following form:
Here k is wave number, 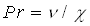 is Prandtl number and is Prandtl number and  is Rayleigh number. is Rayleigh number. 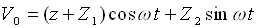 and and  are coefficients, the prime means differentiation on cross coordinate z. For definition of a boundary of stability for a basic flow it is possible to apply Floquet method. The periodic solution was obtained with the help of Galerkin - Kantorovich method. The space basis was constructed with the help of eigen-functions of a problem about disturbances in a motionless layer. are coefficients, the prime means differentiation on cross coordinate z. For definition of a boundary of stability for a basic flow it is possible to apply Floquet method. The periodic solution was obtained with the help of Galerkin - Kantorovich method. The space basis was constructed with the help of eigen-functions of a problem about disturbances in a motionless layer.
The solution was found in a form of a superposition of space basic functions with time-dependent amplitudes. In expansion it was retained up to 16 functions. The time-dependent amplitudes were determined by means of Runge-Kutta method. Multiplicators were defined, and by interpolation there was found the critical value  at fixed other parameters. at fixed other parameters.
In the limits of high frequencies the instability is stipulated by stratification of a liquid in a vibrating field. A boundary of stability is defined by the critical value  from averaged equations. It is connected with vibration Rayleigh number with the help of the relation: from averaged equations. It is connected with vibration Rayleigh number with the help of the relation: 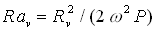 . Neutral curve on a plane ( . Neutral curve on a plane (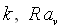 ) in the considered regions of parameters have a minimum at wave number ) in the considered regions of parameters have a minimum at wave number  . At . At 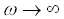 the critical values aim for asymptotic ones which according to the averaged approach the critical values aim for asymptotic ones which according to the averaged approach  , ,  . Dependence . Dependence 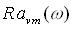 is nonmonotone, it has a minimum at is nonmonotone, it has a minimum at  . In opposite limiting case of low frequencies we have . In opposite limiting case of low frequencies we have 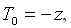  . Thus, for basic condition we receive slowly-oscillating flow, consisting from two counter flows with cubic velocity profile. In static case the stability of such flows is investigated in detail2. In zero on w order we receive the threshold of stability from a integral relation: . Thus, for basic condition we receive slowly-oscillating flow, consisting from two counter flows with cubic velocity profile. In static case the stability of such flows is investigated in detail2. In zero on w order we receive the threshold of stability from a integral relation: 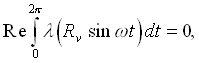 where l is complex decrement of the most dangerous mode in a problem of stability of counter flows with a cross gradient of temperature. It is found, that in limit where l is complex decrement of the most dangerous mode in a problem of stability of counter flows with a cross gradient of temperature. It is found, that in limit 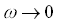 : :  at at 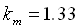 . .
In the intermediate values of frequencies there are regions of parametric excitation. The period of neutral disturbances in these regions coincides with a period of vibrations. The real and imaginary parts of the disturbances have a various period oscillations in neighboring regions: - they coincide, or differ in two times.
In gravity field threshold of the convection is determined by interaction of two mechanisms of the instability: thermogravitational and thermovibrational. The critical Rayleigh number in the absence of vibrations  is 106.7. The influence of longitudinal vibration of finite frequency on convective stability is investigated. At small is 106.7. The influence of longitudinal vibration of finite frequency on convective stability is investigated. At small 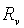 the dependence the dependence  = =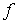 ( (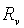 ) is parabolic: ) is parabolic: 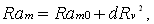 here here 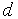 depends on the other parameters. At depends on the other parameters. At  we have we have  , if , if  and and  if if 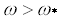 , where , where 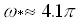 . At moderate . At moderate 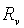 boundaries of the instability on the plane boundaries of the instability on the plane  have a maximum at some have a maximum at some 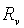 and at concerning high frequencies all curve go into the negative and at concerning high frequencies all curve go into the negative  region, they correspond to heating from above. region, they correspond to heating from above.  In the case of infinite frequencies vibrational mechanism decreases the threshold of the convection. Contrary to the case In the case of infinite frequencies vibrational mechanism decreases the threshold of the convection. Contrary to the case 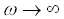 at the finite frequencies parametric effect can stabilize or destabilize of the equilibrium depending on frequency and amplitude of vibration. at the finite frequencies parametric effect can stabilize or destabilize of the equilibrium depending on frequency and amplitude of vibration.
- Gershuni G..Z., Zhukhovitsky E.M. , Dokl. AN SSSR, Vol. 249, No. 3, pp. 580-584, 1979.
- Gershuni G. Z., Zhukhovitsky E.M., Nepomnyashchy A.A. Stability of convective flows.: Nauka, M: 1989.
EFFECTS OF DIFFERING FORCING FUNCTION MODELS ON THE FLOW PAST AN OSCILLATING CYLINDER IN A UNIFORM LOW REYNOLDS NUMBER FLOW
M.TUTAR, A.E.HOLDĈ
CFD RESEARCH GROUP
FACULTY OF ENGINEERING
UNIVERSITY OF HERTFORDSHIRE
HATFIELD, HERTS
AL10 9AB
ENGLAND
Fluid - structure interactions have a large number of practical applications. The modelling of such problems are therefore of some interest. The typical application involves either flow induced or forced oscillations of bluff bodies exposed to a fluid flow and is found in many fields of engineering. Examples are sub-sea ocean pipe lines or risers and off-shore platform supports exposed to ocean currents. A further example is a suspension bridge in a strong wind. The present study deals with the modelling of a circular cylinder in a fluid stream undergoing forced transverse oscillations. Several experimental and numerical studies of flow past oscillating bluff bodies are available in literature [1-5]. The latter studies[4-5] suggest that the numerical modelling of these problems can yield useful results.
The emphasis of the present paper is on the effect of applying the forced transverse oscillations in different manners. Choices of application method may be restricted in the practical application case, and the aim of the present work was to investigate the effect of the differing methods and their range of application. In order to avoid effects due to turbulence models, the simulation is of the viscous two dimensional flow past an oscillating circular cylinder at a Reynolds number of 80 as described in reference [8]. The free-stream flow is modelled to have a uniform velocity. Boundary conditions representing the forced transverse oscillations in the numerical simulations are applied in the following two different ways. In the first case sinusoidal velocity slip conditions are implemented on the cylinder surface[6]. The implication is that no modification or additional body force term has to be added to the Navier-Stokes equation.
In the second case extra body forces are added to the Navier-Stokes equations. This results in a standard no slip condition over the complete cylinder surface. This approach allows a moving reference frame to be treated as a fixed Eulerian reference frame. This negates the difficulties associated with solving time dependent problems using Arbitrary Lagrangian and Eulerian formulations ( ALE ) [7]or Lagrangian methods.
Both models are exposed to varying forcing function frequencies. These frequencies have been chosen both below and above the lock-in range. The Reynolds number and the frequency range was also chosen to comply with available experimental results and observations [8].
The results from the present numerical approaches were found to be in good agreement with each other at low force driving frequencies below and near lock-in. However, differences were found at the higher frequency ranges above lock-in. The computed mean drag results were also compared with Tanidas experiments[8] as seen in Figure 1. These results were again found to be in agreement with experimental observations below and near by lock-in. As the oscillation frequency increases beyond lock-in, mean drag results of the slip case (case 1) deviated from both experimental and the body force results (case 2). Explanations are offered for the differences between the methods and between the numerical results and the experimental observations at the higher frequencies.
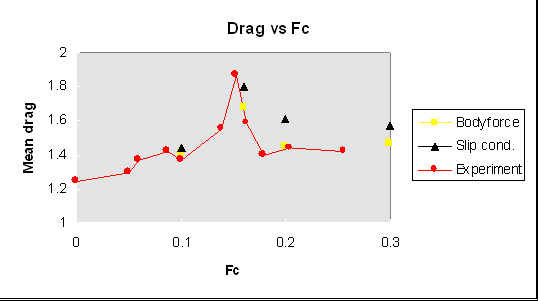
Figure 1. Comparison of mean drag results extracted from Tanidas experiment and two forcing function models versus oscillation frequency at Re=80, A/D=0.14.
REFERENCES
- O.M.Griffin and S.M.Ramberg, Vortex Shedding from a Cylinder Vibrating in Line with an Incident Uniform Flow, J.Fluid Mech., 75(2), 257-271, (1976).
- O.M.Griffin and M.S.Hall, Review-Vortex Shedding Lock-on and Flow Control in Bluff Body Wakes, ASME Journal of Fluids Engineering, 113, 526-537 (1991).
- P.W.Bearman , Vortex Shedding from Oscillating Bluff Bodies, Ann. Rev. fluid Mech., 6,195-222, (1984).
- R.Chilukuri, Incompressible Laminar Flow Past a Transversely Vibrating Cylinder,ASME Journal of Fluids Enginnering, 109,166-171 (1987).
- S.E.Hurlbut, M.L.Spaulding, and F.M.White, Numerical Solution for Laminar Two Dimensional Flow About a Cylinder Oscillating in a Uniform Stream, ASME Journal of Fluids Engineering, 104,214-221 (1982)
- J.Sun, and J.Li and B.Roux, Flow Regimes and Frequency Selection of a Cylinder Oscillation in an Upstream Cylinder Wake, International Journal For Numerical Methods in Fluids, 16, 915-929 (1993).
- R.Wei, A.Sekine and M.Shimura, Numerical Analysis of 2D Vortex Induced Oscillations of a Circular Cylinder, International Journal For Numerical Methods in Fluids, 21,993-1005 (1995).
- Y.Tanida, A.Okajima, and Y.Watanabe, Stability of a Circular Cylinder Oscillating in Uniform Flow or in a Wake, J. Fluid Mech., 61,769-784, (1973).
|

