|
Session 2
NATURAL CONVECTION I
Chairman: Y. Jaluria
A NUMERICAL STUDY OF THE EFFECTS OF CORIOLIS AND CENTRIFUGAL FORCES ON BUOYANCY DRIVEN FLOWS IN A VERTICAL ROTATING ANNULUS
Anthony Randriamampianina*, Eddie Leonardi** and Patrick Bontoux*
*Département de Modélisation Numérique
Institut de Recherche sur les Phénomènes Hors Equilibre
Unité Mixte de Recherche CNRS 138
1, rue Honnorat, 13003 Marseille, France
** School of Mechanical and Manufacturing Engineering
University of New South Wales, Sydney, Australia 2052
ABSTRACT
A detailed understanding of flows in rotating systems is primary concern to many industrial and scientific applications such as turbomachinery, driven solidification from melts, isotope processing by the use of a gas centrifuge and computer disk drives.
In this paper the effect of Coriolis and centrifugal body forces on the stability of the flow and thermal fields for air contained between two vertical concentric cylinders and two horizontal planes is investigated. The inner cylinder is cooled and the outer cylinder is heated. All surfaces are rotating with the same rotational speed.
For the particular configuration Fowlis and Hide1 observed four distinct regimes of hydrodynamical flow, only one of which is characterized by symmetry about the axis of rotation. Such flows can be characterized by four non-dimensional groups viz., AR = H/(Ro-Ri), Q
= gHD
r
/r
W
2(Ro-Ri)2, Ta = 4W
2(Ro-Ri) 5/Hn
2 and Pr = n
/a
.
The unsteady Navier-Stokes and energy equations, expressed in a rotating frame of reference are solved for axisymmetric and non-axisymmetric flow regimes. The coupling between the dynamic and thermal fields is done using the Boussinesq approximation, applied to the Coriolis, centrifugal and buoyancy forces. The numerical approach is carried out with a pseudospectral collocation Chebyshev method, with Fourier series in the azimuthal direction for the fully three-dimensional flows, associated with a second-order accurate time scheme resulting from the combination of Adams-Bashforth and second order Backward Euler schemes. Thus, at each time step, the system of equations to be solved is reduced to the resolution of successive Helmholtz and Poisson equations. By using a complete diagonalization of operators, the solution is obtained from simple matrices products. For the axisymmetric flow regimes, the flow structure in the meridional plane is computed via a vorticity-stream function formulation, using an influence matrix technique to manage the coupling between these variables. For the non-axisymmetric regimes, a primitive variable formulation of the problem is solved using an efficient time-splitting algorithm2.
The numerical technique is first validated by comparison with the experimental results of Fowlis and Hide1 for a water-filled annulus of AR = 3.397.
A detailed study is then undertaken on the onset of non-axisymmetric flows for an air-filled annular enclosure for a range of Ta and Q
. Our main objective is to delineate as accurately as possible the limits between the axisymmetric and non-axisymmetric regimes for air. Particular attention is focused on the transition between the symmetrical regimes (upper and lower) and the steady waves regime.
REFERENCES
- Fowlis, W. W. and Hide, R., Thermal Convection in a Rotating Annulus of Liquid : Effect of Viscosity on the Transition between Axisymmetric and Non-Axisymmetric Flow Regimes, J. Atmos. Sci., Vol. 22, pp 541-558, 1965.
- Hugues, S. and Randriamampianina, A., An Improved Projection Scheme Applied to Pseudospectral Methods for the Incompressible Navier-Stokes Equations, Submitted to Int. J. Num. Meth. Fluids, 1997.
DOUBLE DIFFUSIVE NATURAL CONVECTION IN ENCLOSURES WITH HEAT AND MASS DIFFUSIVE WALLS
V. A. F. Costa
Departamento de Engenharia Mecânica
Universidade de Aveiro, 3810 Aveiro, Portugal
INTRODUCTION
There is a considerable number of numerical studies concerning on the double diffusive natural convection in two-dimensional enclosures. However, such studies are typically devoted to a single cavity with two adiabatic and impermeable horizontal walls, and two vertical walls of constant temperatures and concentrations, which are thus treated as heaving infinite heat and mass diffusivities. In the case of building materials of internal cellular structure, with confining walls which are not perfect insulators nor perfectly impermeable, the heat and mass transfer parameters as well as the temperature and concentration fields are affected by the presence of such walls. Additionally, when assembled in a building, such elements are not isolated but exchanging heat and mass, influence that should also be considered. An important point not usually explored is the visualization of the paths followed by the heat and mass flows through the assembling, including its diffusive walls, using the heat and mass lines.
The present work deals with the numerical simulation of the double diffusive natural convection occurring in a vertical stack of square enclosures with (all) heat and mass diffusive walls. Assuming a spatial periodicity in the vertical direction, the vertical stack is analyzed from the study of a single enclosure communicating with its adjacent enclosures through the top and bottom half separating walls. It is thus a problem of simultaneous conjugated heat and mass transfer with periodic boundary conditions. Once obtained the problem’s solution, special emphasis is devoted to the conjugated problems for the heat and mass functions, from which are obtained the heat and mass lines used for visualization purposes.
PHYSICAL AND NUMERICAL MODELING
The enclosure under analysis is filled with a Newton-Fourier-Fick perfect mixture of a fluid and a pollutant, which flows in laminar regime and doesn’t experience any phase change. For the properties, only the density in the gravitational term is variable, which is taken as a function of both the temperature and concentration through a Boussinesq-type approach. The exterior faces of the vertical walls are maintained at constant temperatures and concentrations. With  over the exterior face of one wall and over the exterior face of one wall and  over the exterior face of the other wall the heat and mass buoyancy effects are combined, while with over the exterior face of the other wall the heat and mass buoyancy effects are combined, while with  or or  over the exterior face of one wall such buoyancy effects are opposed. over the exterior face of one wall such buoyancy effects are opposed.
The problem is solved in its dimensionless form using the control-volume finite-difference method of Patankar,1 with backward staggered grids for the velocity components and the power-law scheme to integrate the convection-diffusion terms. At the solid-fluid interfaces, the combined conjugated heat and mass transfer problems are solved using the harmonic mean practice for the respective diffusion coefficients. The pressure-velocity link is established through the SIMPLER algorithm. The discretization equations for each dependent variable are solved iteratively by successive applications of the TDMA algorithm over crossed horizontal and vertical directions. Due to the spatial periodicity in the vertical direction, it is used a cyclic version of the TDMA algorithm when solving for temperature and concentration fields in such direction.
For visualization purposes are used the heat and mass lines, which are the contour plots of the heat and mass functions.2 Equating the second order derivatives of temperature and concentration appearing in the first order derivatives defining the heat and mass functions one obtains second order PDE’s for such functions. Over the medium that fills the cavity they are Poisson-type equations, while over the solid walls they are Laplace-type equations. As the heat and mass functions are defined through their first order derivatives, such functions exhibit a relative nature similar to that of the pressure field in incompressible fluid flows, with a total freedom when choosing their reference values at a point. Choosing this point over a boundary, the evolution of such functions over the boundaries are obtained by integrating the heat and mass flows over the boundaries, starting from the reference point. To the author’s knowledge, there is no work considering such a conjugated problem for the heat and mass functions.
The heat and mass function fields are obtained assuming that they are conserved variables in order to use the same routines used for the temperature and concentration fields. Due to the nature of the involved PDE equations, this is a conduction-type problem. The diffusion coefficients for the dimensionless heat and mass functions are, respectively, the inverses of the diffusion coefficients for the dimensionless temperature and concentration equations. At the solid-fluid interfaces, the conjugated problems for the heat and mass functions are solved using once again the harmonic mean practice for the respective diffusion coefficients. It should be noted that, due to the nature of the heat and mass functions, the periodic boundary conditions in the vertical direction are not valid for such variables. The contour plots of the heat and mass functions are the heat and mass lines, which are the best picture for the heat and mass transfer processes occurring in a cavity and in the vertical stack.
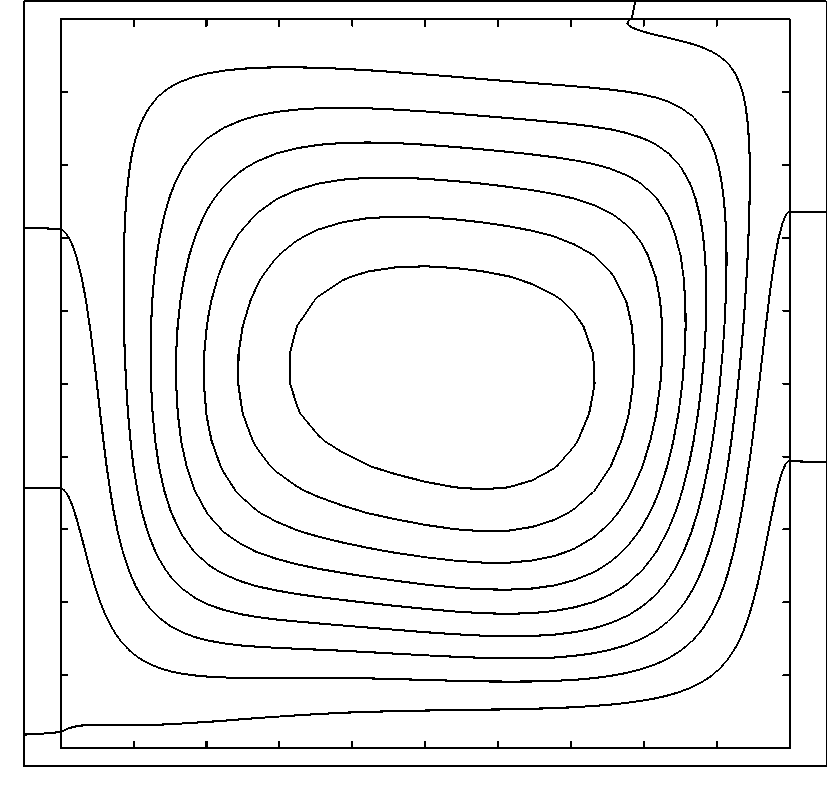
Fig.1. Isotherms (__), isoconcentrations (__), heat lines (__) and mass lines (__) for combined buoyancy effects: (a) Rc=0.1, Rd=0.1, N=0.5; (b) Rc=0.5, Rd=0.5, N=0.5; and (c) Rc=1.0, Rd=1.0, N=0.5.
RESULTS AND CONCLUSIONS
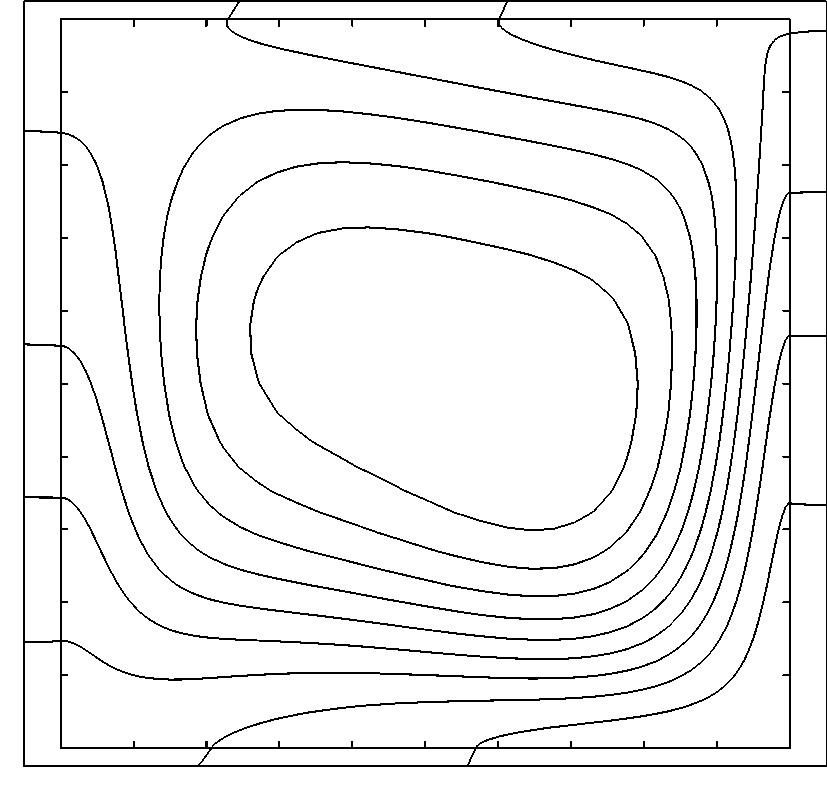
A very short set of results is presented in Figs. 1 and 2, in the form of isotherms, isoconcentrations and heat and mass lines, for the situation of a square enclosure with  filled with moist air filled with moist air  for for  . The remaining important parameters are the buoyancy ratio . The remaining important parameters are the buoyancy ratio  , the heat and mass diffusion coefficient ratios , the heat and mass diffusion coefficient ratios  and and  , and the combined or opposed buoyancy effects. It is used a , and the combined or opposed buoyancy effects. It is used a  non -uniform grid with 7 rows of nodes over each solid wall. The main objective is to show the influence of the diffusive walls over the heat and mass transfer parameters of the vertical stack of enclosures, as well as the power of the heat and mass lines to visualize the simultaneous conjugated problems for heat and mass transfer. non -uniform grid with 7 rows of nodes over each solid wall. The main objective is to show the influence of the diffusive walls over the heat and mass transfer parameters of the vertical stack of enclosures, as well as the power of the heat and mass lines to visualize the simultaneous conjugated problems for heat and mass transfer.
As main conclusion, the heat and mass function conjugated problems can be solved using the same procedures used when solving for the usual conserved variables, including the harmonic mean practice for the diffusion coefficients. Additionally, the heat and mass lines show to be a very effective way to visualize the involved coupled transfer phenomena.
(a)
(b)
Fig.2. Isotherms (__), isoconcentrations (__), heat lines (__) and mass lines (__) for opposed buoyancy effects: (a) Rc=0.1, Rd=0.1, N=0.5; and (b) Rc=1.0, Rd=1.0, N=0.5.
REFERENCES
- Patankar, S. V., Numerical Heat Transfer and Fluid Flow, Hemisphere/McGraw-Hill, Washington D.C., 1980.
- Trevisan, O. V. and Bejan, A., Combined Heat and Mass Transfer by Natural Convection in a Vertical Enclosure, ASME J. Heat Transfer, Vol. 109, pp 104-112, 1987.
DOUBLE-DIFFUSIVE NATURAL CONVECTION IN POROUS MEDIA:
HYDRAULIC ANISOTROPY
R. BENNACER and A. TOBBAL
Laboratoire Matériaux et Sciences des Constructions
de l'Université Cergy-Pontoise, Rue d'Eragny,
95031 Neuville sur Oise cedex, France
This work deals with the numerical study of double diffusive natural convection in a two dimensional cavity filled with saturated porous medium. The vertical walls of the cavity are submitted to thermal and compositional gradients and the horizontal walls are adiabatic. The Darcy-Brinkman formulation equation and co-operating buoyancy forces are taken into account. The porous medium is assumed to be hydrodynamically anisotropic. The influence permeability anisotropy on flow, heat and mass transfer is studied. The evolution of the heat and mass transfer with hydraulic anisotropy shows the existence of three regime : diffusive, convective and channelling convective. The effect of buoyancy ratio (N) on the different regimes are also studied.
Introduction
When multicomponent fluid is subject to density gradients due to local variations of temperature and concentration, buoyancy forces are induced in the fluid and convectif flow take place. Natural convection is of fundamental importance in many natural and industrial problems.
Most of existing studies on convective heat transfer in porous medium are based on the Darcy flow model and isotropic characteristics. Darcy's law is acknowledged to be inadequate in several problems (industrial and natural fields). The thermal and hydraulic anisotropy are generally the consequence of a preferential orientation or asymmetric geometry of the grains or fibbers and different ways connecting the channels. Both types of anisotropy are often coupled in order to understand the basic phenomena : This study is concerned with the hydraulic anisotropy (for thermal anisotropy see Bennacer and Tobbal1 ).
The previous works have been summarised in a recent book by Nield and Bejan2. We can characterise two situations: In the first situation, the stability of convective flow in horizontal layers with imposed vertical temperature or/and concentration is studied. The second one concerns the vertical porous medium with horizontal gradients. In pure thermal convection, isotropic and anisotropic porous medium are analysed. Recently attention has been focused on heat and mass transfer in isotropic porous media.
The present study on heat and mass transfer in anisotropic porous media, takes the Darcy-Brinkman equation into account. In the following section, we will present the mathematical formulation and the basic principles of numerical procedure. The numerical results are presented in section 3 and the conclusion and the interests in section 4.
Formulation and numerical method
Mathematical formulation
The equation for mass, energy, species and momentum conservation in porous media and boundary conditions may be written in dimensionless form as follows.
In the above equations, the classical dimensionless numbers characterising the thermal natural convection are: the aspect ratio A = H / L, the Prandtl number Pr = n
/ a
and thermal Grashof number GrT = b
TgD
TH3 / n
2. The solutal one is defined by: the Schmidt number Sc = n
/ D, the solutal Grashof number Grs = b
sgD
CH3 / n
2 or by the buoyancy ratio N = Grs / GrT=b
sD
C/b
TD
T and the Lewis number Le =Sc/Pr.
| Equations | | Boundary conditions
| |
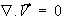
|
(1) |
u = 0, q
= 0.5, f
= 0.5 at X = 0 (5) |
|
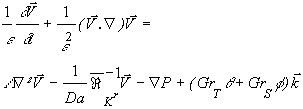
|
(2) |
u = 0, q
= -0.5, f
= -0.5 at X = 1/A (6)
|
|
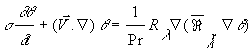
|
(3) |
w=0,  at Z=0 and Z=1 (7) at Z=0 and Z=1 (7) |
|
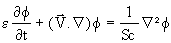
|
(4) |
|
The porous characteristics are: the Darcy number Da=Kz / H2, the relative conductivity
Rl
= l
z / l
f, the ratio of viscosity to the fluid viscosity in the Brinkman term L
, the specific heat
s
= (r
c)eq / (r
c)f. The porous thermal Rayleigh number Ra*, defined as: Ra* = GrT.Pr.Da will be used in the analysis of the results. Thermal and hydrodynamic anisotropy of the porous medium are represented respectively by the dimensionless second order tensors:
 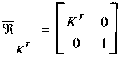
In order to obtain heat and mass transfer in dimensionless form we have defined reference diffusive fluxes (mass :  , heat : , heat : ). The average values on vertical plane are : ). The average values on vertical plane are :
the Nusselt/Sherwood number: 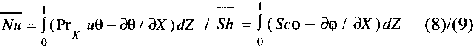
Numerical Method
The finite volume procedure used in this work is derived from the technique proposed by Patankar3. The equations are integrated over the corresponding control volumes, leading to a balance equation for the fluxes at the interfaces. A hybrid scheme is used to discretise the equations. The pressure-velocity coupling in the momentum equation need iterative procedure based on a pressure correction method (for faster convergence SIMPLER algorithm Patankar3 is coupled to the SIMPLEC algorithm Van Doormaal and Raithby4, for more details: see Bennacer5 ).
Numerical experiments were performed to establish the number and the distribution of the control-volumes required to represent accurately the thinnest boundary layer, the numerical results presented in this paper are given using at least 61´
61 sinusoidal grid. The convergence criterion is based on both maximum error of continuity equation and the average quadratic residual over the whole domain for each equation and convergence is reached when the maximum error is less than 10-6.
Numerical results
The validation of the numerical code was performed over a large range of parameters for purely thermal fluid natural convection, for the isotropic porous medium and for the anisotropic porous medium 6.
We studied the influence of the hydraulic anisotropy on heat and mass transfer, the range explored is 10-3 £
Kr £
103 for different Darcy number, different buoyancy forces (N) and different Lewis number.
The evolution of the average heat transfer (Nu) with the hydraulic anisotropy (Kr), for different N and given Rayleigh porous number ( Ra*=103 ) and Le=10, is given in Figure 1. This figure clearly shows the existence of tree distinct regimes : diffusive one (low Kr) fully convective (channelling regime high Kr) and mixed one (moderate Kr). The flow structure clearly shows the diffusive regime where the iso-temperature and iso-concentration are vertical and the channelling regime where the flow takes place especially in the vertical porous layer. It appears on this figure that for higher N the transition between different regimes occurs for lower Kr which is the consequence of stronger flow.
The tree different regime has been analysed by Ni and Beckermann7 in pure thermal convection.
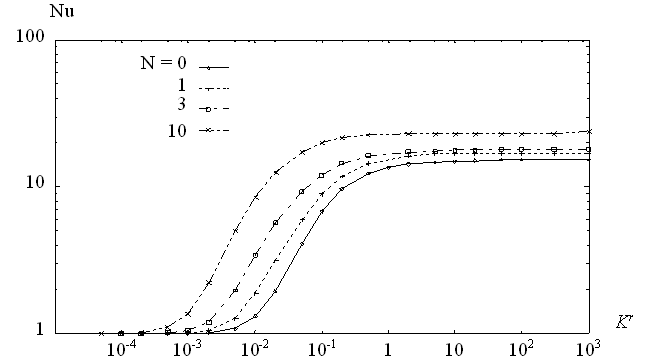
Figure 1: Average Nusselt number vs. hydraulic anisotropy for different N (A=1, Ra*=103, Le=10)
Conclusion
In this study we have presented a numerical study on double diffusive natural convection in anisotropic porous media. The effect of hydraulic anisotropy on mass transfer has been analysed and three different regimes of flow and transfer have been found. The transition between different regime depends on N, Lewis number and the porous Rayleigh number.
Bibliography
- R. Bennacer, A. Tobbal : Coupled Heat and Mass Transfer in Vertical Anistropic Porous Layer. Heat Transfer 96 : Fourth International Conference on Advanced Computational Methods in Heat Transfer. 493-502, Udine, Italy, 8-10 July 1996.
- D.A Nield and A Bejan, Convection in Porous Media, Springer. New York, 1992.
- Patankar S.V., Numerical heat transfer and fluid flow, Hemisphere. New York, 1980.
- Van Doormaal J.P. and. Raithby G.D, Enhancements of the SIMPLE method for predicting incompressible fluid flows, Num. Heat Transfer, 7,147 1984
- Bennacer R., Convection naturelle thermosolutale : simulation numerique des transferts et des structures d'ecoulement, Thèse Université Paris 6, 1993.
- Tobbal, R. Bennacer, R. Cabrillac and H. Beji, Etude numérique de la convection naturelle double-diffusive dans une cavité poreuse anisotrope utilisant la formulation de Darcy-Brinkman submitted to Int. J. Heat Mass Transfer.
- J. Ni and C. Beckermann, Natural convection in a vertical enclosure filled with anisotropic porous media, J. Heat Transfer 113, 1033-1037 (1991)
INTERACTIONS BETWEEN THE MARANGONI AND INTRUSION FORCES IN A MULTI-CAVITY SYSTEM
M.Z.Saghir*, M. Hennenberg**, J.C. Legros*** and M.R. Islam****
*Dept of Mechanical Eng, UAE University, Al-Ain, U.A.E.
** Chimie-Physique, Faculté des Sciences, U.L.B, Belgium
*** Microgravity Research Center, Faculté des Sciences Appliquées, U.L.B, Belgium
****Dept of Chemical and Petroleum Engineering, UAE University, Al Ain, U.A.E
INTRODUCTION
This paper numerically investigates the interaction between the Marangoni convection, the double diffusive convection and the intrusion force in the Maxworthy1 set-up. The model consists of a two-cavity rectangular system in which the smaller cavity is located at the top left corner of the larger one. The larger cavity is filed with hot salty fluid while the smaller one contains cold fresh fluid. This problem is solved for the case of the fresh water intruding into the salty water. The interaction between the Marangoni (thermal and solutal) and the double diffusive regimes is investigated in detail. Finite element modelling results indicate that salinity induces stronger convection than the thermal ones and the thermal and solutal Marangoni convection further enhances the strength of the cellular flow. Numerical results indicate that surface force should be taken into consideration during the analysis and that the intruding force played an important role in the flow behaviour.
The problem was solved for two different cases. In the first case, the interaction among the intrusion force, the thermal Marangoni force and the double diffusive convection were studied. In the second case, the solutal Marangoni convection was added to the system leading to a more realistic case. This particular case is closer to the set-up that Maxworthy1 used in his experiment. Tanny et al2 studied the interaction between the double diffusive and the surface tension gradient phenomena by heating the bottom of the cavity. They carefully set up their experiment to avoid any free surface contamination. It is well known that the surface tension varies linearly with temperature and concentration3,4. The problem was solved for a Rayleigh number RaT=104. The Prandtl number Pr was set equal to 10. The Lewis number Le, was set equal to unity. In addition, the ratio of the thermal diffusivity in the horizontal and vertical direction was assumed to be equal to unity. Another dimensionless parameter, the Turner number (Rr
), was set equal to unity.
RESULTS AND DISCUSSIONS
Figure 1 shows the schematic of the model and the boundary conditions used in this analysis. At time t =0, the fresh water is injected to the salty cavity at a velocity U (U= u/uo). The initial temperature and concentration differences, between the salty and the fresh water, are set equal to unity. At the free surface the velocity in the x direction is not equal to zero. However, the velocity in the y direction is set equal to zero and, therefore, no free surface deformation will occur
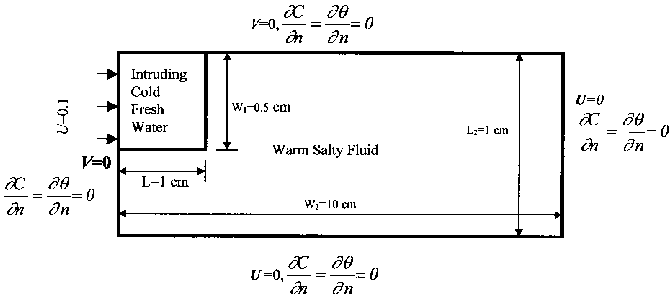
Figure 1. Boundary Conditions of the Model.
Thermal Marangoni Convection. The streamline and the concentration contours are shown in Figure 2. The streamline contours show that strong convective cells are formed from the beginning of the numerical experimentation. If one examines the flow pattern carefully, one may notice that two separate flow patterns are forming. The first is due to the double diffusive and the Marangoni convection that create counter-clockwise cells. The second is the flow generated by the injected fluid. Since the latter one has lower velocity magnitude (i.e low flow rate), it is pressed towards the bottom of the cavity. However, momentum is added to the injected fluid from the convective cells and moves the fresh injected fluid to the end of the cavity. It is at this end that the fluid overflows the cavity and is designated as a singularity point. Finally, the overflow fluid is mainly salty fluid since the concentration at this point, for this particular time, is still equal to unity.
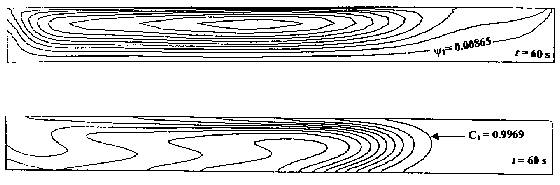
Figure 2. Streamlines and Concentration Contours due to the Thermal Marangoni Convection. (t = 60 s D
y
=0.0206,D
C=0.0061)
Combined Thermal and Solutal Marangoni Convection. In order to study a more realistic case, both the thermal and the solutal Marangoni convection were included in the model. Figure 3 displays the concentration and the streamline contour plots at a time t=7.5s. In the previous case, the thermal Marangoni was moving the flow in counter-clockwise direction, thus adding to the double diffusive force against the intruding force. In the present case, the combination of the thermal and solutal Marangoni convection moves the flow in the clockwise direction. From Figure 3, one can observe that the intruding force together with the combined Marangoni convection moves in the clockwise direction against the double diffusive effect this time. The fresh water is moved to the end of the cavity and then pushed backward towards the salty region. It is clear that the intruding forces enhanced the strength of convection. In summary, one can notice an active competition between the double diffusive force in one side and the combination of the intrusion force, the thermal and the solutal Marangoni forces.
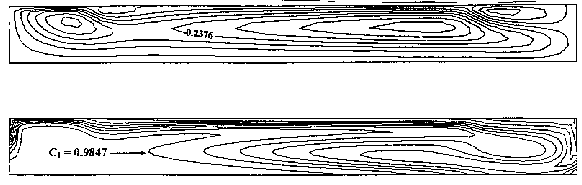
Figure 3. Streamlines and Concentration Contours due to the Thermal and the Solutal Marangoni Convection at t = 7.5 s (D
y
=0.0709, D
C=0.0305)
REFERENCES
- T. Maxworthy, The Dynamics of Double Diffusive Gravity Currents, J. Fluid Mech., 128, 259-282, 1983.
- J. Tanny, C.C. Chen and C.F. Chen, Effects of Interaction between Marangoni Convection and Double Diffusive Instabilities, J, Fluid Mech, Vol 303, 1-21, 1995.
- J. Li, J. Sun and M. Z. Saghir, Buoyant and Thermocapillary Flow in Liquid Encapsulated Floating Zone, Journal of Crystal Growth, Vol 131, 83-96, 1993.
- M.Z. Saghir, R. Abbaschian and R. Raman, Numerical Analysis of Thermocapillary Convection in Axisymmetric Liquid Encapsulated InBi, of Crystal Growth, Vol 169/1, 110-117, 1996.
|

