SESSION 6

PLASMA DIAGNOSTICS

INTRODUCTION

Although probe techniques have been available for many years for plasma diagnostics, they have been getting a wider acceptance over the past ten years. The most important of theses are the langmuir and enthalpy probes. Enthalpy probes can be used for the simultaneous measurement of the locale specific enthalpy, velocity and composition of the plasma. Their main advantage is the simplicity of the technique, and its possible use for the simultaneous measurement of multiple plasma parameters with a generally acceptable special resolution. Its main limitation, however, is that it is an intrusive technique, with the probe inevitably causing a local perturbation of the flow. Enthalpy probe techniques can not be used either for time-resolved measurements. A brief description is given in this paper of the use of enthalpy probes for the characterization of a supersonic induction plasma jet.

BASIC CONCEPTS

A schematic of the setup used for enthalpy probe measurements in an induction plasma jet is given in Figure 1. This consists essentially of a triple wall probe cooled by a high pressure, deionized, closed loop, water circuit. The specific enthalpy of the plasma is determined through a measurement of the difference between the heat load on the probe cooling circuit under sampling and tare conditions.

where m_w is the cooling water flow rate, Cp_w is the specific heat for the water, m_g is the sample gas flow rate. DT_sample and DT_tare are the temperature rise of the cooling water under sampling and tare flow conditions. Knowing the specific enthalpy of the plasma, h_o, and its composition, x_o, the plasma temperature can be calculated using available thermophysical data. From a measurement of the dynamic pressure on the probe tip, the local plasma velocity can be calculated as follows:

For incompressible flow: where (Po-) is the measured dynamic pressure, and r is the local plasma density computed at the local plasma temperature, T_o, and composition, x_o.

For compressible flow, an interactive procedure has to be used for the solution of the following equations relating the ratio of the local impact pressure, Po to the chamber pressure, , with the local Mach Number, Mo, with with , R=universal gas constant, and T_o the absolute plasma temperature.

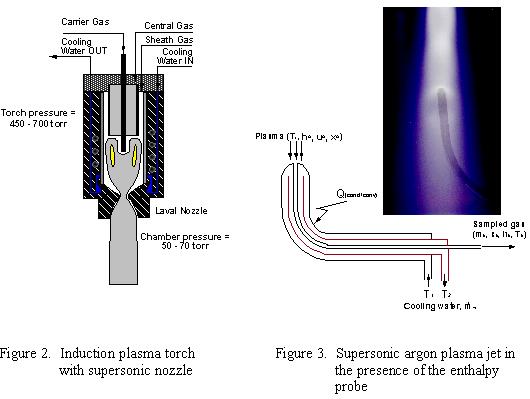
SUPERSONIC INDUCTION PLASMA TORCH

Supersonic flow is achieved using a standard PL-35 Tekna plasma torch through the addition of a Laval type nozzle at the exit of the torch as shown in Figure 2. A photograph of an argon plasma jet in the presence of a 4.78 mm diam. Enthalpy probe is given in Figure 3.

TYPICAL RESULTS

Typical radial profiles obtained at an axial location, z = 25 mm, downstream of the nozzle exit, for the local plasma temperature, velocity, Mach number and dynamic pressure, are given in Figure 4. These were obtained with a Mach 1.5 nozzle with a throat diameter of 12.8 mm and an expanded jet diameter of 13.8 mm. The plasma gas was in this case an Ar/H₂ mixture with 2% vol. H₂. The plate power of the r.f. power supply was 25 kW, with a corresponding r.f. power coupled into the plasma of about 16.25 kW. The absolute pressure in the discharge chamber was 17.1 kPa with the back pressure in the torch cavity of 36.3 kPa. It is noted that a maximum centerline Mach number of 1.0 is obtained on the centerline of the torch with a corresponding local plasma velocity of almost 1500 m/s. The local plasma temperature in this region was about 5500K. Measurement carried out for the same plasma gas mixture with a Mach 3.0 nozzle, at an axial location, z = 17 mm, from the nozzle exit, gave rise to an increase of the local Mach number on the axis of the discharge to 2.0 with a corresponding local plasma velocity of 2000 m/s and a centerline temperature of 2500K.

D.C. plasma torches have been involved for many years in industrial applications such as welding, cutting or deposit elaboration by plasma spraying or plasma assisted vapor deposition.

These techniques use specific properties of plasmas produced by D.C. arcs, where high temperature (up to 25000 K) and high flow velocities (up to few km/s) are available. A considerable amount of experimental work was devoted, in the past, to characterize the properties of arc jets as a function of arc current, torch design or configuration, plasma forming gas thermophysical properties and flowrate. In the same time models approached more and more accurately the behavior of arc jets, testifying of a real advance in both knowledge and understanding of the different implicated processes and mechanisms.

Nevertheless, mainly because of experimental difficulties, transient phenomena due to arc instabilities have been less intensively studied and their interest has only been underlined the last decade, altough they have been mentionned more than thirty years ago.

Due to the extraordinary progress accomplished in the field of instrumentation, new diagnostic techniques have raised, accompanied by powerful signal processing methods which are now easy to apply thanks to the development of computers and associated softwares.

It has been experimentally demonstrated in plasma torches that the arc is submitted to gas dynamic forces which give rise to different modes of instabilities among which to major cases can be distinguished. The first one is the so-called «take-over» mode, characterized by rather low fluctuations of arc voltage compared to the mean value, the second one being the «restrike» mode, for which the fluctuations of arc voltage are about the same in amplitude than the mean value. The restrike mode is clearly identified as the result of the stretching of the arc by the cold gas flow, followed by electrical breakdown of the cold gas layer which give rise to a new arc-anode attachment. The stretching-rearcing sequences is repeated at a frequency which is governed by experimental conditions and give a saw tooth-shaped voltage signal, which analysis provide clear informations about the arc dynamics.

The fluctuation of arc length generate strong voltage variations which are correlated to the electrical power supplied to the gas and, as a consequence, to the variations of the arc jet temperature and velocity.

The amplitude and frequency of voltage fluctuations can be related to the torch working and geometrical parameters and dimensional analysis allow to establish reliable semi-empirical correlations. Temperature and velocity distributions are strongly correlated to the torch working conditions and the resulting fluctuations. It will be illustrated for different operating conditions of a D.C. spray toch.

INTRODUCTION

Interaction of plasma jets with an ambient atmosphere play an important role in plasma processing applications, e.g. in plasma spraying or treatment of hazardous waste. Entrainment of cold gas in thermal plasma jets was studied by several methods^l-3. It has been shown in the foregoing authors papers^4-5 that the application of the array of several electric probes is a relatively simple and efficient tool for local investigation of structure of flow field in the thermal plasma jets. Electric probes measurements are used in this paper for the investigation of characteristics of turbulence arising in the interaction zone of the plasma jet with the ambient air.

EXPERIMENTAL SETUP The experiment was performed with the plasma jet generated by plasma torch with water stabilized electric arc. The total power of the torch was varied in the range 90 - 200 kW. Thus, the development of turbulence was investigated for mean exit plasma velocity in the range 1700 to 4200 m/s6. The array of 6 probes made of Mo wire with diameter 1 mm and length 1 mm was moved through the plasma jet with velocity less than 1.5 m/s at different positions downstream of torch exit. The probes were positioned 3-7 mm apart with various mutual arrangements. The probes were negatively biased and were operated in ion collecting part of the probe characteristics. They were connected to the source of biasing voltage through the resistor. The values of the resistance and the voltage were adjusted to obtain high sensitivity of the probe signal to plasma properties. Strongly fluctuating probe signals were obtained when plasma disturbances flowed along the probes tips. The maps of the probe current contours in coordinates corresponding to radial position and time represent the structure of the plasma flow. RESULTS Plasma flow structure in the jet was investigated for various arc currents and various plasma flow velocities. Fig. 1 shows an example of a map of the same probe currents in the boundary zone of the jet. Almost periodic structure of the boundary was observed along the jet with regions of cold gas entrained into the plasma jet and regions of plasma propagating into the surrounding gas. From these maps obtained by statistical analysis of measured probe signals at different positions along the jet following characteristics of flow in the jet bouridary were determined (Fig. 1): mean axial distance of regions of cold gas in the jet L=vtL, mean axial dimension of cold gas regions D=vtD and mean depth H of entrainment of gas into the jet. The velocity v was derived from the shift of signals of two probes located in different axial positions. Characteristic dimensions L, D and H were dependent on arc current, i.e. on plasma flow velocity which is determined by arc current, and on axial position in the jet. Fig. 2 shows the dependence of ratio of the depth H to the mean radius of the jet R on the distance from the nozzle exit for two values of arc current. It can be seen that the depth of entrainment H is larger for smaller arc currents, i.e. for lower temperature and energy content in the jet and for lower flow velocity. The characteristic dimensions of the entrainment rapidly increase with the distance form the torch exit. ACKNOWLEDGEMENT Financial support from the Grant Agency of the Academy of Sciences CR under project No. A1043804/1998 and from the Grant Agency of the Czech Republic under project No. 102/98/0813 is gratefully acknowledged.

REFERENCES

• Pfender E., Fincke J., Spores R.: Plasma Chem. and Plasma Proc. 11 (4), 1998, 529.
• Russ S., Pfender E., Strykowski P.J.: Plasma Chem. and Plasma Proc. 14 (4), 1994, 425.
• Fincke J.R., Chang C.H., Swank W.D., Haggard D.C.: Int. J. Heat Mass Transfer 37 (11), 1994, 1673.
• Kopecky V.: Electric probes investigation of turbulence in the interaction zone of the plasmajet with the ambient air. 1998 ICPP&25^th Conf. on Contr. Fusion and Plasma Physics, Praha, ECA Vol. 22C, 1998, 2643 - 2646.
• Hrabovsky M., Konrâd M., Kopecky V.: Investigation of structure of turbulent boundary layer between thermal plasmajet and ambient air. 5^th European Conference on Thermal Plasma Processes, St. Petersburg, 1998 (in press).
• Hrabovsky M., Konrâd M., Kopecky V., Sember V., Processes and properties of electric arc stabilized by water vortex, IEEE Trans. on Plasma Science 25 (1997), No. 5, pp. 833-839.

The study of microscopic particles behaviour under corona discharge was earlier based on several basic concepts. More particularly, DC corona discharge was investigated by the way of developing electrostatic precipitators^1-3 (ESP) employed in air and gases cleaning processes. Inside one stage ESP, microscopic particles are charged both by diffusion and by field charging mechanisms, and then, collected on the electrode of opposite sign. Design of ESP's is usually based on the Deutsch formula for turbulent flows in the case of instantaneous mixing. But, when focus is on space distribution (local concentration of particles) in a given geometry, one should resolve Electro-Hydro-Dynamic equations stated in the general case of dense flows4. In the case of dilute flows, the appropriate convection-diffusion equation is considered to draw the particle concentration field.

In this work, the convection-diffusion equation is resolved in the case of wire-cylinder configuration, using realistic boundary conditions^5-7. A finite differences method is then used to compute the particle concentration field (fig.1) versus the axial position (z* = z/R), and the particle concentration gradient (fig.2) versus the radial position (r* = r/R), considering the geometric particle diameter (d_P) as a parameter. This last figure, shows a maximum of the gradient in the range r* = 0.15 to 0.3. Furthermore, the maximum of the fractional gradient moves with respect to particle size (d_P) and radius position (r*) depending on the electrical charging mechanism. When the diffusion mechanism becomes powerless, the strength of the electrical force is relatively reduced and consequently the maximum of fractional gradient decreases. In the range of sub-microscopic particles, the tendency is opposite due to the presence of both charging mechanisms. Notice that the minimum corresponds to 0.2 µm and not to 0.1 µm.

In order to verify the assumption of dilute flow (no particle-particle interaction and no coalescence phenomenon when treating atmospheric aerosols), the particle size distribution is computed using the same numerical code. The experimental distribution is obtained on a laboratory ESP (radius R = 17 mm and length Z =1020 mm for the collection electrode, and
0.15 mm radius for the wire electrode) using an optical counter probe under isokinetic conditions (Re~9000, U = 4.2 m.s^-1). Electrostatic conditions are : 11 kV for the wire discharge voltage and 8 mA/m² ionic current density. As illustrated on fig.3, comparison between numerical and experimental results tends to confirm the previous assumption over the range [0.5 - 2.0 µm].

Fig.1 : concentration field versus axial position z*	Fig.2 : concentration gradient versus radial position r* at z* = 10 (z = 10R).
Fig.3 : Bar graph of both numerical and experimental particle size distribution

REFERENCES

• Parker C. Reist, Aerosol Science and Technology, McGraw-Hill, 2nd edition, 1993.
• Ogawa A. , Separation of particles from air and gases, CRC Press, 2nd printing, 1985.
• Williams J. C. and Jackson R., The motion of solid particles in an electrostatic precipitator, Interaction Between Fluids and Particles, Instn. Chem. Engrs., London, pp. 282-288, 1962.
• Yamamoto T., Verkoff H.R., Electrohydrodynamics in an Electrostatic Precipitator. J.Fluid Mech., 108, 1-18, 1981.
• Leonard G. L., Mitchner M. and Self S. A., Particle transport in electrostatic precipitators, Atmospheric Environment, Vol. 14, pp 1289-1299, 1980.
• Shaughnessy E. J., Davidson J. H., and Hay J. C., The fluid mechanics of electrostatic precipitators, Aerosol Science and Technology, Vol. 4, pp. 471-476, 1985.
• Li Enliang, Wang Yingmin, and Raper J. A., Study of gas velocity distribution in electrostatic precipitators, Aerosol Science and Technology, Vol. 12, pp. 947-952, 1990.

In order to obtain deposit with the desired properties, the influence of plasma spraying parameters on the flow and the coating was often studied. Nonetheless, if a lot of parameters (arc current, total gas flow rate, gas composition) can be kept constant during the spraying, it is not the case of the arc voltage, which can be influenced by two phenomena. The first one is the electrode erosion (which can be reduced by the use of Ar/He/H² gas mixtures) resulting in a decrease of the plasma momentum and a variation of the particle behavior in the plasma jet. This variation can be corrected by increasing the power of the torch (arc current or the percentage of hydrogen). The second phenomenon is mostly difficult to correct : it is the movement of the arc inside the nozzle implying fluctuations of the arc voltage and the plasma flow.

Several studies have analysed the dynamic behavior of DC plasma gun for binary gas mixtures Ar/H₂ or Ar/He, for which the range of variation of gas composition is too limited. Indeed, it is well known that a high hydrogen content results in a quicker erosion of the electrodes, and helium content must to be high enough to melt particles. Ternary gas mixtures, reducing electrode erosion, permit the use of a large range of gas composition, which can be adapted to the required properties of the deposit. Nonetheless, the use of Ar/He/H₂ gas mixtures results in a modification of the plasma/particule tranfert, flow and stability of the gun working, which can result in a modification of the atmosphere engulfment in the plasma jet.

This paper presents an investigation of the influence of the plasma spraying parameters on the fluctuations of arc root, arc voltage and plasma flow. The measurements were carried out for various ternary gas mixtures of argon, helium and hydrogen (Table I).

Table I : Plasma spraying conditions.

The fluctuations of the arc voltage and plasma flow are controlled respectively by the analysis of the voltage signals and plasma velocity. This latter is measured by using the analysis of the luminous fluctuations of the plasma flow. In the potential core, the plasma jet velocity was determined from the light fluctuations which originate in the arc root instabilities. These fluctuations are supposed to propagate at the flow velocity. The measurement method is closely connected to a time-of-flight method.
The measurement of arc voltage fluctuations are based on the analysis of the arc restrike behavior in DC plasma torches. The sampling rate is 10 µs/point (100 kHz), higher than the arc root frequency (4 to 20 kHz).
Experiments were carried out using a Plasma Technik F4VB gun with a 6-mm nozzle diameter and a vortex injection of the plasma forming-gas in the arc zone.

• From the arc voltage signals, the effect of total mass gas flow rate, gas composition and arc current on the static behavior of the plasma spray torch was studied :
  • the average arc voltage
  • the arc root frequency
  • the jump amplitude which is the deviation between the minimum and maximum voltage within an oscillation
  From an adimensional analysis, a correlation between the frequency, and the plasma spraying parameters was established, showing that it is similar to the plasma velocity correlation established previously.
• Concerning the analysis of the dynamic behavior of the torch, for higher total gas mass flow rate (>5.10-4 kg/s), only the restrike mode was observed, due to the major influence of the mass flow rate (which depends on the gas composition and the plasma temperature) on the arc movement. The influence of hydrodynamic forces on arc root is predominant.
  For lower total gas mass flow rate (< 5.10-4 kg/s), several modes of torch working have been observed for a low gas mass flow rate, explained by the significative influence of electromagnetic forces on the arc root :
  • an oscillating mode (Fig. 2)
  • a restrike mode (Fig. 3)
  • an intermediate mode (Fig. 4).

Figure 2 : Arc voltage signal (in volt) in the oscillating mode (Ar/He/H2 gas mixture : 50/40/10 vol. % - 27 slm - 320 A).	Figure 3 : Arc voltage signal (in volt) in the restrike mode (Ar/He/H2 gas mixture : 40/40/20 vol. %.- 27 slm - 600 A).
Figure 4 : Arc voltage signal (in volt) in the intermediate mode (mélange Ar-He-H2 : 37/55,6/7,4 % vol. - 27 l/mn - 320 A)

This article have shown that the restrike mode is obtained when the hydrodynamic or/and electromagnetic forces, and thickness of the cold layer surrounding the arc column are sufficient to produce the jump of the arc attachment.
The experiments pointed out the fact that at a low gas mass flow rate, with the increase of the anode erosion, the restrike mode disappears. Indeed some preferential arc attachment points are created on the anode surface, and thus the hydrodynamic forces are no longer sufficient to produce arc jump.
The analysis of the plasma velocity fluctuations gives us information on the stability of the gun working. It appears that this stability is higher in the case of higher constricted arc column and a mass flow rate.

ABSTRACT

Plasma jets generated by conventional d.c. plasma torches reveal more or less severe temporal fluctuations due to fluid dynamic effects and the effect of anode arc root motion inside the plasma torch. As shown in the frames of Fig. 1, the fluctuations cause the jet characteristics to continuously change with time during torch operation. They, in turn, alter trajectories and temperature histories of the particles which are injected into the fluctuating plasma jet. The resultant particle behavior is somewhat different from the one obtained under steady-state plasma conditions. Although there is clear experimental evidence for the existence of such fluctuations¹, previous simulations of plasma jets usually neglected such fluctuations, because of the difficulties associated with the analytical description of their transient and three-dimensional characteristics. Moreover, it is time-consuming to simulate the fluctuations using a transient three-dimensional code, even with high-speed parallel supercomputers. Any realistic comparison of experimental data with analytical predictions, however, requires that such fluctuations should be considered in the modeling efforts, because experimental data will usually provide time-averaged and fluctuation-averaged values.

In this paper analytical/numerical studies of the particle behavior in plasma jets are reported, taking these plasma fluctuations into account in a simplified manner without developing a transient three- dimensional code. In general, the arc root moves back and forth in axial direction, and it also rotates along the cylindrical anode surface with a fluctuation frequency in the order of several kHz. The plasma plume, therefore, experiences axial and radial fluctuations according to the arc root motion. The rotational fluctuations are approximated by radial fluctuations assuming that the arc root attaches itself on the anode surface without any preferred tangential direction. The radial fluctuations can be simply included in the numerical model for simulating plasma jets by the time- averaging method².

In the time-averaging method the steady-state solutions for plasma jets are obtained using conventional two-dimensional codes such as the LAVA code³. The steady-state plasma variables such as velocity and enthalpy are allowed to fluctuate in radial direction with specified fluctuation distance and frequency. By averaging those fluctuating variables over a fixed fluctuation period, new time-averaged plasma conditions can be found, leading to plasma variables comparable to the experimental data. However, before considering particle injection into the plasma under time-averaged conditions which are obtained using the time-averaging method, we have to consider particle residence time. The residence time of powder particles in the plasma jet is typically longer or of the same order of magnitude as the fluctuation period. This implies that the particles are actually interacting with a fluctuating plasma rather than with an axisymmetric time-averaged plasma. In order to take these fluctuation-dependent interactions between plasma and particles into account in the model, the steady-state plasma solutions are allowed to fluctuate in radial direction and the powder particles are injected into the fluctuating plasma jets.

The re-strike mode of torch operation results in plasma fluctuations in axial direction as well as in radial direction. The axial fluctuations manifest themselves through voltage fluctuations. The voltage variation leads to changes of the input power and the plasma jet characteristics vary with the imposed input power. The voltage variations directly affect the boundary conditions at the torch exit. The maximum axial velocity and temperature values change with the voltage fluctuations since we assume that the profile shapes are fixed at the torch exit. In this paper, the voltage is assumed to fluctuate sinusoidally with the same frequency as the radial fluctuations. Figure 2 presents plasma temperature distributions which are varying with time under the influence of both axial and radial fluctuations during one fluctuation period. A single particle or multiple particles are injected into these axially and/or radially fluctuating plasma jets to study the effects of plasma fluctuations on particle behavior.

CONCLUSION

The effects of the plasma fluctuations on the motion and temperature histories of a single particle and multiple particles are investigated in the present paper. Comparisons of particle data based on steady-state plasma conditions obtained without considering the fluctuations show large deviations from the corresponding experimental data. On the other hand, the particle data obtained with consideration of axial and radial plasma fluctuations reveal reasonable agreement with measurements. The simple features of the proposed analytical way of taking into account the plasma fluctuations can be easily applied to conventional plasma and plasma-particle interaction models.

REFERENCES

• S. A. Wutzke, "Conditions governing the symptomatic behavior of an electric arc in a superimposed flow field," Ph.D. Dissertation, University of Minnesota, 1967.
• J. H. Park, "Numerical modeling of multi-component plasma jets," M.S. Thesis, Department of Mechanical Engineering, University of Minnesota, 1998.
• J. D. Ramshaw and C. H. Chang, "Computational fluid dynamics modeling of multicomponent thermal plasmas," Plasma Chem. Plasma Proc. 12, 299 (1992).

Fig. 1 Pictures of a fluctuating plasma jet taken by a laser strobe camera

Fig. 2 Temperature distributions of a plasma jet fluctuating in axial and radial directions