SESSION 10
INVERSE RADIATION PROBLEMS I
INVERSE PROBLEMS OF RADIATIVE TRANSFER IN ABSORBING,
EMITTING AND SCATTERING MEDIA
M.N. Özisik and J.C. Bokar
North Carolina State University
Mechanical and Aerospace Department
Raleigh, NC 27695-7910 U.S.A.
This work reviews and summarizes the current state-of-the-art techniques
utilizing the Levenberg-Marquardt method, conjugate gradient method and a
combination of both for solving inverse problems in radiative transfer.
Illustrations are given in order to show the utility of each, as applied to
function, parameter and property identification. We also examine the effects of measurement errors on the accuracy of estimations by inverse analysis.
In high temperature systems, radiative transfer is the fundamental mode of heat
transfer. In most engineering applications the properties, the boundary
conditions and the source terms in the medium are assumed to be known and the
radiation flux or intensities are calculated. Such problems are referred to as
the direct problem. However, if one or more of the properties or source terms
unknown and measured radiation intensities are available, an inverse solution
technique can be formulated in order to estimate the unknown quantity. This
paper is intended to give an overview of the Levenberg-Marquardt method,
conjugate gradient method and a combination of both in the solution of inverse
problems of radiation transfer in participating media.
Recently, several inverse problem techniques that have come to the forefront in the radiative transfer field have their beginning in the solution of inverse
problems of heat conduction. They include, among others, the conjugate
gradient, Levenberg-Marquardt methods, a combination of the previous two and
the Monte Carlo technique. These algorithms have been applied in such problems
for the estimation of source terms and boundary conditions, properties,
scattering phase function and simultaneous radiation and conduction problems.
In this paper we will focus on the conjugate gradient and Levenberg-Marquardt
methods for parameter and function estimation.
INVERSE PROBLEM TECHNIQUES
Several methods are currently being applied for solving the inverse radiation
problem. Each method is best applied to a particular type of inverse problem as discussed below.
The Levenberg-Marquardt Method This technique is used solely for
parameter estimation. It is a combination of a steepest descent and Newton’s
methods for minimization type problems. The method requires the minimization
of the least squares norm functional and the solution of the sensitivity
problem. The number of parameters to be solved for should not be too large as
instabilities may emerge in the iteration process. The method is accurate, can
handle nonlinear parameter identification, but generally needs a good starting
estimate of the unknown parameters in order to achieve convergence.
The conjugate gradient method This method also uses the least squares
norm and requires sensitivity coefficients as was described in the
Levenberg-Marquardt technique. The conjugate gradient method can be applied to
both parameter and function estimation problems. When the problem involves
parameter estimation, we need only the sensitivity problem. When a function is
to be estimated, however, an adjoint variable with a gradient equation must
also be used in the analysis. The technique allows for initial estimates of
unknown parameters or functions far from the final converged results.
The combined method For parameter estimation problems, the
Levenberg-Marquardt and conjugate gradient methods may be combined in
situations where a satisfactory initial guess value can not be found with the
Levenberg-Marquardt method. The new algorithm uses the conjugate gradient
method of solution in order to provide an initial estimate for use as the
initial guess for the Levenberg-Marquardt method. The only drawback may be the
extra time involved for programming.
EXAMPLE PROBLEMS
Problem #1 Conjugate Gradient Method for Parameter
Identification
We begin with a problem that will utilize the conjugate gradient method for
parameter identification for an absorbing, emitting and isotropically
scattering plane parallel medium. The problem consists of the equation of
transfer for isotropic scattering. The boundary conditions are with one
boundary reflecting and the other transparent. The objective of the analysis is to estimate the unknown coefficients an of a volumetric source term represented as a polynomial and unknown reflectivity of the boundary surface from measured
exit intensities.
Problem #2 Combined Levenberg-Marquardt and Conjugate Gradient Method
(parameter)
This problem is concerned with the estimation of a temperature source term
represented as a polynomial in an absorbing, emitting and isotropically
scattering sphere using a combined conjugate gradient and Levenberg-Marquardt
method in the sense that the converged solution of the conjugate gradient
method provides the initial guess for the Levenberg-Marquardt method which is
then iterated until the final converged solution is obtained.
Problem #3 Conjugate Gradient Method as Function Estimation
This problem illustrates the estimation of an unknown volumetric source term
represented in functional form. The conjugate gradient method with adjoint
equation is best suited for function estimation. We apply this method in order
to determine an unknown temperature source term in an absorbing, emitting and
anisotropically-scattering plane-parallel medium using measured exit radiation
intensities.
INVERSE RADIATIVE ANALYSES TO DETERMINE RADIATIVE
PROPERTIES USING TEMPERATURE WAVE METHOD
Andrei V. Galaktionov
Institute for High Temperatures Russian Academy of Sciences
13/19 Izhorskaya, Moscow, 127412, Russia
A universal technique based on the temperature wave method is described for
nondestructive determining the spectral radiative properties at high
temperatures. The temperature wave method requires pulse-periodic laser heating
of a sample, and the measurements of thermal radiation on examined wavelengths,
and the digital spectral analysis of laser power indicator and radiometer
signals. The simplest case of non-scattering half-infinite medium with
translucent mirror boundary and with small impact of radiative heat transfer on temperatures waves is considered in detail as an example. Thermal diffusivity
of the sample is taken as known. The absorption coefficient on wavelength of thermal emission as well as on wavelength of excitation are to be determined from the experiment.
The sensitivity of the inverse problem to experimental errors is numerically
examined without its full solving. The inverse problem is based on the
approximation of the measured frequency response function of the sample by the
theoretical one on several initial harmonics of basic frequency of the laser
heat action. The approximation is carried out using the non-linear least
squares method. The random error theory of the inverse problem is a combination of classical random process theory and well-known theory of the least square
method. The sensitivity is calculated using the singular value decomposition of the design matrix. The design matrix is calculated by numerical derivation of
theoretical frequency response function of the sample with respect to
determined parameters.
Optimal parameters of the pulse-periodic laser heating are evaluated.
Sensitivities of several kinds of the temperatures waves method are compared.
The method is contrasted with known techniques of photo-thermal radiometry.
INVERSE RADIATIVE HEAT TRANSFER TECHNIQUE FOR HEAT FLUX
RESTORATION USING OPTIMAL WIENER FILTRATION
Alexander I. Ilyinsky
Chemical Engineering Department, Ege University, 35100, Bornova,
Ízmir, Turkey
The spatial distribution of energy on the treated surface should be known for
better control in many applications in laser and solar technologies and
material science. The increasing heat losses due to radiation, convection and
conduction may change or reduce thermal efficiency of material processing. This paper presents a new technique for restoration of heat flux1
distribution for the sheet material using temperature measurements with random
errors. Let us consider the thin wall with radiative heat flux distributed on
the external side and cooling by convection on the internal side. Due to finite thickness of the wall conduction redistributes heat fluxes and the direct
application of the Fourier law to estimation of heat fluxes on the surfaces is
impossible.
The asymptotic methods have been used to reduce 3D problem into 2D formulation
for thin wall and the zero approximation of 3D transient conduction equation
can be written in form
 (1)
where x, y - coordinates on the wall, k- thermal conductivity,d- thickness of
the wall, with right side term q containing difference of heat fluxes on
external and internal sides of wall. the heat flux restoration algorithm is
based on the spectral analysis of 2-D discrete Laplacian operator with data
filtration in frequency domain using optimal Wiener filtration and quasi-Wiener filtration.
The proposed algorithm of radiative heat flux restoration can be described by
following step-by-step instruction:
- The initial measured temperature data Ti,j* are
converted into Fourier components
 n,m*by standard 2-D sine FFT.
- The fourier components n,m* are filtered by an appropriate 2-D
low pass Wiener filter with frequency response wfn,m
- Calculate the corrected values of heat flux' harmonics
 n,m*F
by:
- The recovered heat flux distribution qi,j*F is
obtained by inverse 2-D sine FFT of the corrected harmonics n,m*F
Estimations of radiative heat fluxes have been obtained for different wall
thickness of the sensor and different signal to noise ration in temperature
data. To study the effect of noises on the accuracy of the proposed heat flux
restoration technique, the series of numerical experiments have been carried
out. The initial temperature data and results of restoration are presented in
Fig. 1-2. The accuracy of heat flux restoration technique has been studied both for Wiener and quasi-Wiener filtration and the simple practical criterion of
selection of a regularization parameter has been proposed.
The reported results demonstrate the main features of new heat flux estimation
technique; its simplicity, high rate of processing, stability and adequate
accuracy and spatial resolution. The developed algorithms can be used for study of interaction of an incident radiative heat fluxes with the thin walls and
creates new opportunities for radiative heat transfer measurements.
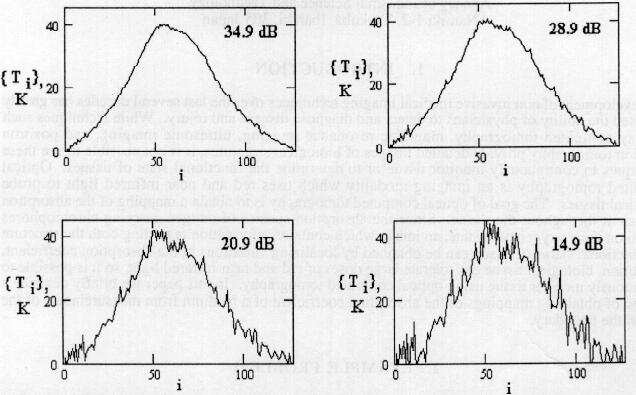
Figure 1. Temperature distributions measured with errors at different
averaged SNR.
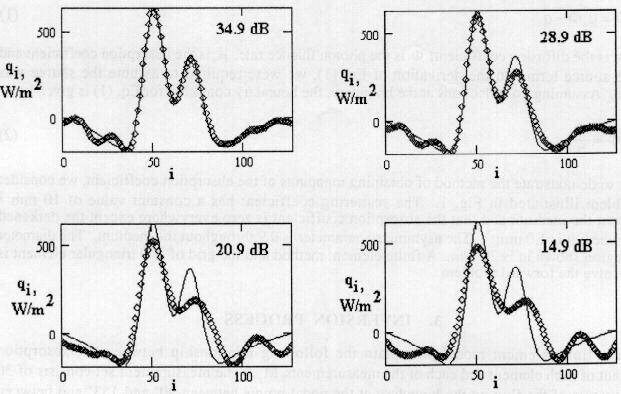
Figure 2. Heat flux restoration with Wiener filtration for different
averaged SNR points - restored data - exact distribution
AN INVERSION TECHNIQUE FOR OPTICAL COMPUTED
TOMOGRAPHY
Matthew R. Jones, Yukio Yamada, and
Akira Tezuka
Biomechanics Division
Mechanical Engineering Laboratory
Agency of Industrial Science and Technology
Namiki 1-2, Tsukuba, Ibaraki, 305 Japan
1. INTRODUCTION
The development of non invasive medical imaging techniques over the last
several decades has greatly increased the ability of physicians to detect and
diagnose disease and injury. While techniques such as x-ray computed
tomography, magnetic resonance imaging, ultrasonic imaging, and positron
emission tomography provide detailed images of biological structures, it is not possible to use these techniques to continuously monitor tissue or to determine the functional state of tissues. Optical computed tomography is an imaging
modality which uses red and near infrared light to probe biological tissues.
The goal of optical computed tomography is to obtain a mapping of the
absorption coefficient throughout the tissue. Since the absorption spectra of
oxygen carrying chromophores depend on their oxygenation state, an image which
contains information regarding both the structure and functional status of
tissue can be obtained by localizing variations in the absorption coefficient.
In addition, biological tissue can tolerate large doses of red and near
infrared light, so it is possible to continuously monitor tissue using optical
computed tomography. In this paper we briefly describe a method of obtaining
mappings of the absorption coefficient of a medium from measurements of the
flux on the boundary.
2. EXAMPLE PROBLEM
Light propagation in highly scattering, weakly absorbing medium such as
biological tissue is often described using the diffusion or P1 approximation to the radiative transfer equation. The time independent photon diffusion equation is given by
 (1)
where  is the diffusion
coefficient,  is the
photon fluence rate,  ais the absorption coefficient and q is the source
term. In the derivation of Eq. (1), we were required to assume the source was
isotropic. Assuming no reflections at the boundary, the boundary condition for
Eq. (1) is given by
 (2)
In order to demonstrate the method of obtaining mappings of the absorption
coefficient, we consider the problem illustrated in Fig.1. The scattering
coefficient has a constant value of 10 mm-1 throughout the medium
and that the absorption coefficient is zero everywhere except the darkened
region, where it is 1.0 mm-1. The asymmetry parameter is 0.9
throughout the medium. The diameter of the region shown in is 20 mm. A finite
element method and the grid of 800 triangular element is used to solve the
forward problem.
3. INVERSION PROCESS
Using the finite element model we obtain the following relationship between the absorption coefficient of each element and each of the measurements,
Mp. The measurement set consists of 30 measurements of the flux on
the boundary at the nodal points between 90o and 153o
and between 207o 270o.
 (3)
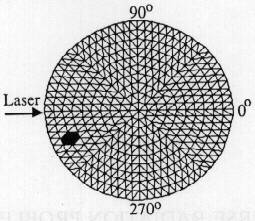
Figure 1. Finite Element Model
In Eq. (3) Ai is the absorption coefficient from
the previous iteration and the Jacobian matrix, J, represents the sensitivity
of the pth measurements to changes in the absorption coefficient of
the qth element. Assuming that the absorption coefficient is
initially zero everywhere, we obtain successive approximations by inverting Eq.
(3) until convergence is obtained. However, since the number of elements is
much larger than the number of measurements, Eq. (3) represents a highly
underdetermined system of equations if we vary the of every element. We overcome
the underdetermined nature of the problem by grouping the elements into blocks
and varying the absorption coefficient of each element in a block by the same
amount. Unfortunately this process also greatly reduces the resolution of the
mapping. We are able to increase the resolution of the mapping by using what we
call the zooming method. In the zooming method we initially group all the
elements into large blocks and obtain a low resolution mapping. We then
concentrate the blocks in regions where inhomogeneities appear to be present,
hold the absorption coefficient constant outside the region of interest, and
repeat the solution process. Equation (3) is inverted using the singular value
decomposition of the Jacobian matrix.
4. RESULTS
Figure 2 shows how resolution of the absorption coefficient mapping is improved by using the zooming method. The mapping on the left hand side was obtained
when all the elements were grouped into 36 blocks which contain between 16 and
27 elements each. The mapping in the middle was obtained using 30 blocks
containing 2 or 3 elements each. The mapping on the right hand side was
obtained using 21 blocks which contain only one element each.
Figure 2. Absorption Coefficient Mappings
|
