SESSION 2
SOLUTION OF RADIATIVE TRANSFER EQUATION I
R. Koch*+, W. Krebs*,
S. Wittig*, R. Viskanta**
*Lehrstuhl und Institut fü Thermische
Strömungsmaschinen
Universität Karlsruhe, Karlsruhe, Germany
**School of Mechanical Engineering
Purdue University, West
Lafayette, U.S.A.
Among the various methods proposed for numerically solving the radiative
transfer equation, the discrete ordinates method is presently judged as one of
the most promising. The usual procedure in the method is to solve one first
order differential equation for each of the discrete directions. The numerical
treatment of these first order differential equations is well known for its
convenient programming and its small computer memory requirements. However,
this approach possesses some major shortcomings. The most serious one is due
to the nature of the differential equations (first order, hyperbolic type). The
method is difficult to implement in advanced finite volume or finite element
codes for combusting flows which are designed to handle complex geometries.
In order to overcome this disadvantage, an alternate methodology based on the
even parity formulation of the discrete ordinates equations is proposed. This
approach leads to a set of second order differential equations as governing
transfer equations. The equations are of the parabolic type and their
structure is formally similar to the differential equation describing a
diffusion process. Hence, this formulation of the discrete ordinates equations
is compatible with the numerical structures employed by computer codes for
combusting flows.
The parabolic formulation of the discretes ordinates method has been
implemented in a computer program for three-dimensional combusting flows
developed at the University of Karlsruhe. The code is based on a finite volume
formulation and can handle complex geometries by using body-fitted,
non-orthogonal grids.
The major objective of the paper is to demonstrate the capabilities of the
method.As basic evaluation, sample calculations of benchmark solutions are
presented. The test cases are defined on a Cartesian coordinates system. The
results reveal that the achievable accuracy of the method is comparable to the
conventional discrete ordinates method.
With respect to the application of curvilinear, bodyfitted grids, special
emphasis is placed on the various effects encountered when a non-orthogonal
grid is used. As a typical example, the rotation of the grid with respect to
the principal coordinates system has been studied. It was found to have an
unexpected effect on the radiative flux distribution. A close examination
reveals that this effect is related to the directional biasing inherent to the
angular quadrature schemes.
Finally, ray effects which are well known to be present in the conventional
discrete ordinates method were studied. It was found that they are also present
within the parabolic formulation of the discretes ordinates method and that
they may be suppressed by applying higher order quadrature schemes.
+ Presently visiting Assistant Professor at Purdue
University
Rodolphe VAILLON, Michel LALLEMAND and Denis
LEMONNIER
Laboratoire d'Etudes Thermiques (URA CNRS 1403)
ENSMA, Site du
Futuroscope, BP 109
86960 Futuroscope, France
Since pioneering works of the 60s (1-2), the Discrete Ordinate Method (DOM)
has become of a widespread use in the heat transfer community during the last
decade. However, it has so far mainly been applied to cartesian geometries and
its extension to curvilinear systems is still limited to cylindrical or
spherical coordinates (3-4-5). In particular, we are not aware of any previous
works where the DOM is implemented for general orthogonal curvilinear
coordinates.
One of the major difficulties of the DOM in non cartesian geometries is the
so-called angular redistribution which appears in the RTE when expressed in a
given direction and then projected over the coordinate axes. Extra directional
terms arise from the fact that the orientation of the local system varies with
the position in the spatial frame. As a consequence, a same direction is seen
under carious angles at different locations. Furthermore, for non cartesian
geometries, the integration of the RTE over a control volume may lead to
incorrect results since the space derivative of a constant intensity will in
general not give zero (6). Thus, it requires a specific task to formulate the
discrete ordinate method in curvilinear coordinates.
A general expression for the pathlength derivative of radiation intensity is
given for spatial directional orthogonal curvilinear coordinates system. The
main steps involved in the DOM are described in the case of the configuration
described in Fig. 1. As an application the DOM is used for solving the coupled
radiative-conductive heat transfer problem in an absorbing-emitting
(but non scattering) gray medium confined between two axisymmetric shells whose
generatrices are either ellipses or paraboles. The chosen thermal boundaries
conditions are temperature or fluxes assessments and the radiative properties
of the shells can be black or diffusely reflectives. The problem is solved for
a set of curvilinear coordinates (s,n) moving along the inner wall.
Results are given in terms of temperature mappings and fluxes profiles for
various values of the optical thickness and of the Planck number.
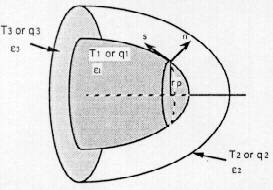 | Fig. 1: the problem under
consideration and its associated curvilinear coordinates system
|
- CHANDRASEKHAR S. -Radiative Transfer. Dover Ed., 1960
- CARLSON B.G and LATHROP K.D. -Transport Theory The Method of Discrete
Ordinates. Computing Method in Reactor Physics, Gordon and Breach 1968
- YÜCEL A. and WILLIAMS M.L. - Azimuthal dependent Radiative Transfer in
Cylindrical Geometry. ASME HTD 72, pp.29-37, 1987
- BOUGUERRA E.H. and LEMONNIER D. - Prediction of coupled
conductive-radiative heat transfer in cylindrical and annular enclosures by SN
methods. Heat Transfer in Semitransparent Media, Ed. Europeennes de Thermique,
pp.165-173, 1992
- JENDOUBI S., LEE H.S and KIM T.K Discrete Ordinates solutions for
radiatively participating media in a cylindrical enclosure. J. Thermophys. Heat
Transfer, Vol.7, pp.213-219, 1993.
- JONES P.D and BAYAZITOGLU Y. Coordinates systems for radiative transfer
equation in curvilinear media. J. Quant. Spect.Rad.Transfer, Vol.48 (4),
pp.427-440, 1992
- VAILLON R., LALLEMAND M. and LEMONNIER D. Radiative-conductive heat
transfer in curvilinear coordinates by the discrete ordinates method.,
EUROTHERM 36, LET ENSMA, Sept. 1994.
Kyeong-Beom CHEONG, Tae-Ho SONG
Department of Mechanical Engineering,
Korea Advanced Institute of Science and Technology,
Kusong-dong 373-1, Yusong-ku, Taejon, KOREA
Radiative heat transfer in a two dimensional square enclosure containing gray
absorbing/emitting and nonscattering media was investigated to explore validity
of the second order discrete ordinates method which had been reformulated from
the conventional discrete ordinates (SN) method. Discretization
equations of governing equation and boundary condition were obtained using a
Taylor series expansion method (TE) and using an exponential scheme with cubic
interpolation method (EXP3) and the results were compared with those from the
conventional SN method and the zonal computations
(in the zonal computations, the direct exchange areas were integrated
numerically using the GAUSS-Legendre quadrature). Two sample problems were
taken; in the first, the medium has known heat source and the walls are cold
(gas emission problem), and in the second, the medium has no heat source and
one of the walls is hot while the others are cold (boundary emission problem);
all the walls are black and diffuse in both problems. The two problems were
solved to obtain the medium temperature and the wall heat flux distributions
using S2 and S6 methods with varying optical depth.
When the optical depth is as small as 0.1, S2 results of the second
order and the conventional discrete ordinates method deviate significantly from
the zonal one in both problems while the S6 results of any discrete
ordinates method are in fair agreement with the zonal results. When the optical depth is large (10 here), the heat flux obtained from S6/EXP3 is
closer to the zonal result than that of conventional S6 near the
corner in both problems.When the optical depth is unity, an intermediate
behavior is observed. On the whole, the second order SN results show very good agreement with those of conventional SN method and when
the number of discrete ordinates is not too small, they also agree well with
the zonal computations. When the optical depth is small in the boundary
emission problem, the second order SN method shows wall heat
flux greater than the blackbody emissive power near the corner
(TE is worse than EXP3), which calls for further improvement.
CALCULATION OF THE RADIATION FLUX DIVERGENCE NEAR THE
REGION OF LOCAL HEAT RELEASE BY QUADROMOMENT METHOD
Sergey T. SURZHIKOV
Institute for problems in Mechanics
Russian Academy of Sciences, Moscow, Russia
Accurate and general solutions of the radiation heat transfer equation in
two-dimensional geometry are required for several low temperature plasma
applications. To study various radiation transfer calculation methods in
two-dimensional cylinder-shaped geometry the stimulating problem is the one of
mathematical simulation of radiation processes in the continuous optical
discharge, which is used in laser plasma generators and laser sustained rocket
engines. As a rule, continuous optical discharge is generated at pressures
around the atmospheric level, therefore, the model of local thermodynamic
equilibrium may be used as the basis for a radiant heat exchange problem. A
typical dimension of the continuous optical discharge is ~1 cm, the temperature
in its central part is ~12000-20000 K.
The radiation transfer equation has been modeled by using method of
quadromoments for two dimensional cylindrical geometry. The scattering of heat
radiation is disregarded.
The original for method of quadromoments was first given by Özışık,
Menning and Halg1 (the half-range method for a spherically symmetric
geometry), Sherman2 (the half-moment method for a plane-parallel
geometry), Mengüç and Iyer3 (the multiple spherical
harmonics approximations for plane-parallel and two-dimensional cylindrical
geometries).
At present formulation, the simplest zero-order moments are used to provide a
solution of the radiation heat transfer equation for two-dimensional
cylindrical volume with high temperature inhomogeneities.
The technique of lowering the order of the system of multigroup equation in the
quadromoment form is described. The problem, in essence, is this: integration
of radiation transfer equation in a selective formulation or in group
approximation (including statistical simulation at sections) for the purpose of
determination of the total energy emission rate stipulated by radiation
processes provides for multiple solutions in individual sectors of the spectrum
with subsequent adding up of the results. This is the main reason for the fact
that the labor intensity of solution of selective radiation transfer usually
supersedes the labour intensity of solution of the associated mechanical
problems. Therefore methods of effective reduction of dimensionalities of the
system of selective equations are often used in radiation gas dynamics. The
common idea of these methods is that the full system of selective equations is
not solved at each stage of solution of gas dynamics equations, but is solved
periodically (as the need arises). The main result of solution of this full
system of equations is determination of effective coefficients in the transfer
equation integrated through the spectrum. It is this last equation that is
solved at each step jointly with gas dynamics equations until the given
replacement of the system by just one equation becomes too rough. The advantage
of the such formulation of the quadromoment method is that unlike methods of
averaging by the full solid angle (for example, PN-approximations of Spherical
Harmonic method), where the average integral absorption coefficient may have
gaps of the second type, the given case presents a smooth continuous
functions.
Numerical solutions of the equations for the two-dimensional cylindrical
geometry are obtained using a software code and the results are compared with
those available by P1-approximation of Spherical Harmonic method. These
calculations were made for two temperature distributions: with temperature in
the hot area centre T1=10000K and
T1=18000K. Different calculation grids, absorption
coefficients k and coefficients defining the value of artificial
calculation diffusion  were
used. It has been established that the zero approximation of the quadromoment
method with =1-10 in a wide
range of optical thicknesses allows to obtain results close to the results
based on the P1 approximation of the spherical harmonics. If
=0.1 is entered, it leads
to incorrect distribution of heat radiative flux divergence in the peripheral
area of the volume. Relative error is getting higher as we move further from
the central high-temperature area.
A question is discussed as to whether the method of quadromoments can describes
the heat radiative flux divergence in low temperature plasma near the regions
of local heat release.
- Özışık, M. N., Menning, J., and Halg, W., Half-range moment method for
solution of the transport equation in a spherically symmetric geometry,
JQSRT, Vol.15, p. 1101-1106, 1975.
- Sherman, M.P., Moment methods in radiative transfer problem, JQSRT,
Vol. 7, No. 1, pp. 89-109,1967.
- Mengüç, M.P., Iyer, R.K., Modeling of radiative transfer using
multiple spherical harmonics approximations, JQSRT, Vol. 39, No.6,
pp.445-461, 1988.
RADIATIVE HEAT TRANSFER OF ARBITRARY 3-D PARTICIPATING
MEDIA AND SURFACES WITH NON-PARTICIPATINGMEDIA BY A GENERALIZED NUMERICAL
METHOD REM2
Shigenao MARUYAMA and Toshio AIHARA
Institute of Fluid Science, Tohoku University, Sendai, Japan
Radiative heat transfer of absorbing, emitting and scattering media and of
diffuse and specular surfaces containing non-participating media is analyzed
by a generalized numerical method: Radiation Element Method by Ray Emission
Model, REM2. Arbitrary thermal conditions can be specified for each
radiation element. A generalized radiative heat transfer analysis can be
achieved without recognizing participating media and surface elements by
introducing the ray emission model and extinction view factors.
We consider a system composed of N radiation elements. N elements
are divided into M participating media or absorbing and diffuse
reflecting surfaces and L non-participating media or perfect specular
surfaces. The radiation elements are numerically modeled by arbitrary
triangles, quadrilaterals, tetrahedrons, wedges and hexahedrons generated by a
general purpose pre- and post-processor package for the finite element
method.
Discretized radiation rays are emitted from each participating radiation
element according to a ray mission model. The ray tracing is performed for all
N radiation elements; however, only M participating elements are
considered for view factors and radiation transfer. In the present analysis,
the elements are classified into participating and non-participating radiation
elements and the memory needed for the calculation is minimized.
The present method was applied to a two-dimensional participating square and a
three-dimensional participating cube covered with black isothermal walls. The
results are compared with a semi-analytical solution and the results obtained
by a zonal method, respectively. The present method shows good agreement with
existing solutions, using only a small number of ray emission and radiation
elements. Comparison of the dimensionless temperature distributions of the
cubic medium show some deviation between solutions for large and small ray
emission numbers. However, the distribution in each case is almost identical
except for the very small region near corners.
A spherical participating medium with uniform heat generation contained in a
square isothermal and adiabatic walls is analyzed. The temperature in the
participating sphere shows spherical distributions for the case of small and
medium optical thickness in spite of the non-spherical boundary conditions of
the outer wall when the heat generation is uniform in the spherical medium.
As an example of an arbitrary configuration, a torus plasma in a large helical
device for the research of a fusion reactor was analyzed, in which plasma is
approximated as a gray participating medium and a specular and diffuse surface
is assumed for the vacuum chamber.
The dimensionless temperature distribution of the model plasma and surface heat
flux of the vacuum chamber are demonstrated. The dimensionless temperature
distribution of the model plasma and the dimensionless surface heat flux are
shown in the Figure below. The analysis model is consist of 2430 elements. The
figure represents the total model of the helical device comprised of 24300
elements and a part of the wall and plasma are removed to show the
distributions. The temperature distribution of the plasma has a maximum value
at the center, and a minimum in the region near the end major axis. The heat
flux on the wall is negative due to the definition. The distribution shows a
maximum flux on the bottom of trapezoidal grooves and has a minimum value at
the corner of the edge of the grooves.
Temperature distributions of modeled plasma in large helical device used for
study of fusion reactor and the wall heat flux on vacuum chamber.
|
