SESSION 8
HEAT EXCHANGERS 2
TRANSIENT BEHAVIOUR OF HEAT EXCHANGERS
Yalçýn A. Göðüþ, O. Ercan Ataer*
Aeronautical Engineering Dept., METU, ANKARA, Turkey
*Mechanical Engineering Department, Gazi University, Ankara, Turkey
Transient behavior of heat exchangers carries great importance because of its effect on overall performance of the systems in which they take place. In this paper a general formulation of the problem, some simple solutions, recent novel approaches and various techniques will be discussed.
NUMERICAL STUDY OF TRANSIENT FORCED CONVECTION IN PARALLEL-PLATE HEAT EXCHANGER
Nadim El Wakil, Mourad Rebay, Jacques Padet
Laboratoire de Thermomécanique - UTAP - SUE
Université de Reims - Champagne Ardenne
B.P. 1039, 51687 Reims, France
A numerical study of transient forced convection in parallel-plate heat exchanger is
presented. The walls are insulated and the separating plate has a negligible resistance. The fluids flow is supposed laminar and fully developed. To obtain the transient effect of the heat transfer, a sudden change of the temperature of one or both fluids is imposed at the entrance. A finite difference method is used to solve the problem. The effect of the nature of the fluids, the heat capacity of the separating plate, the magnitude of the flow rate and the temperature step is analysed. A distortion in the temperature profile and some inverse variations of the temperature near the separating plate are observed in some cases during the transient phase. The duration of the unsteady state depends on the sign of the temperature step.
MODAL ESTIMATES AND STABILITY ANALYSIS OF A HEAT EXCHANGER APLICATION
- A LAPLACE TRANSFORM APPROACH -
P. Ligarius* and N. Mouhab+ and L. Estel+
*Lab. of Control Theory, INSA of Rouen, BP8, 76131 Mont Saint Aignan Cedex, FRANCE.
e-mail: ligarius@insa-rouen.fr
+Lab. PSOPIC, Insa of Rouen, BP8, 76131 Mont Saint Aignan Cedex, FRANCE
e-mail: Mouhab@insa-rouen.fr
We consider here the mixt following problem:
 (1) (1)
with the boundary conditions: U(t,0) = 0 and V(t,l) = 0 (2)
and the initial conditions: U(O,x) = 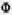 (x) and V(O,x) = (x) and V(O,x) = 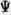 (x) (3) (x) (3)
we give a complete analysis and estimations of the modes of the system which allows prove that its solution w decrease exponentially when time passes by with the rate  for which an explicit estimation is given. for which an explicit estimation is given.
UNSTEADY HEAT TRANSFER MODELING OF HEAT EXCHANGERS
Fernand FRAGNAUD
Laboratoire d'énergétique I.S.I.T.E.M.
La Chantrerie, CP 3023, 44087 Nantes, FRANCE
In unsteady-state heat transfer, one must take into account the heat capacity of the solid material. Here, we take up the problem of the solid walls by a periodic method which gives without simplification the heat transfer across the wall in a form that is very easy to use. Then we only need a spacial partition. In case of a step input, the step responses are well obtained by sommation of a Fourier series.
|
|
|

