KEYNOTE LECTURES
FROM GAS-LIQUID TO LIQUID-LIQUID FLOW: A DIFFICULT JOURNEY?
G. F. Hewitt
Imperial College, London, UK
ABSTRACT
Liquid-liquid flows have assumed much greater importance in recent years in many fields, perhaps
most significantly in the area of petroleum recovery. However, the amount of work which has been
done in this area is dwarfed by the vast range of studies which have been carried out on gas-liquid
flow and it is inevitable that studies on liquid-liquid flow are strongly influenced by the approaches
used in gas-liquid flow work. The objective of this lecture is to evaluate the relevance of these
approaches to this different area.
Modern work on gas-liquid flow is strongly focussed on the delineation of flow patterns and the
development of flow-pattern-specific models. The first subject evaluated in this comparitive
assessment is, therefore, thie issue of flow regime. In liquid-liquid flow, some of the flow regimes
are very similar to those encountered in gas-liquid flow (for example stratified flow and annular
flow) but there are some important differences.Thus, though it has been observed by some workers,
slug flow seems notably elusive in liquid-liquid flows and mixing processes between the two
liquids play a dominant role. The Lecture evaluates the various flow pattern results; a new factor
(hardly considered at all in the case of gas-liquid flows) is the nature of the wetting of the solid
surface of the channel by the respective fluids. It may be concluded that new approaches are needed
to deal with flow pattern prediction in liquid-liquid systems.
In gas-liquid flows, the two-fluid model is the work horse of prediction schemes. Typically,
momentum equtions are written for each of the respective phases and are closed using single phase
flow based friction relationships. It can be shown that such relationships apply only to systems
where the ratio of the viscosities of the two phases is high (as in gas-liquid systems); when the two
viscosities approach each other, the predictions from the two-fluid models depart from those given
by exact solutions. This represents a further important difference between gas-liquid and liquid-liquid
flows. Data for phase holdup and pressure gradient are presented.
Pressure gradients in liquid-liquid flows can display significant peaks when plotted as a function of
water fraction for a given velocity; the response depends on the mixing processes between the
phases. These peaks are associated with phase inversion phenomena.
Evidence is presented and discussed on the influence of the channel wall material on pressure
gradient and phase distribution. This shows the importance of matching the surfaces used in
experiments to those in the projected application.
On the whole, one may conclude that the journey from gas-liquid systems to liquid-liquid systems
is indeed a difficult one!
THE EFFECT OF SURFACE FORCES ON FLOW PATTERNS AND FLOW CHARACTERISTICS IN TWO-PHASE SYSTEMS
Neima Brauner
Dept. of Fluid Mechanics, Faculty of Engineering
Tel Aviv University, Israel
In attempting to explore liquid-liquid flow characteristics and transport phenomena, the
prediction of the flow pattern and the associated spatial distribution of the two-phases is a key
issue.
As in gas-liquid systems, the flow pattern observed depend on the liquids flow rates,
physical properties (viscosity, density and surface tension), tube diameter and inclination.
However, due to the relatively low density differential between the two-fluids, the role of gravity
in liquid-liquid systems diminishes. Therefore, wall-wetting properties of the liquids and surface
tension forces become important and may have a significant effect on the flow pattern. The
liquids-wall wetting is not just a property of the tube material, but depends on the history and
dynamics of the liquids motion near the wall surface. Consequently, start-up procedure and
entrance condition may also affect the flow pattern.
Stratified flow with complete separation of the liquids may prevail for some limited range of
relatively low flow rates where the stabilizing gravity force due to a finite density difference is
dominant. The interface is not necessarily flat. The wetting liquid tends to climb over the tube
wall resulting in a curved (concave or convex) interface.
The characteristic interface curvature has been predicted by employing energy
considerations (Brauner et al, 1995). The controlling non-dimensional parameters are the
fluids/wall wettability angle, 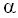 and the Esötviös number. The latter represents the ratio between
surface and gravity forces: and the Esötviös number. The latter represents the ratio between
surface and gravity forces: 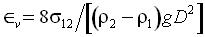 where where 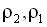 are the fluids densities, are the fluids densities,  is
their surface tension and D is the tube diameter. Stratification with flat interface is realized in
systems of is
their surface tension and D is the tube diameter. Stratification with flat interface is realized in
systems of  -> 0 while for -> 0 while for  >>1, the stratified configuration approaches a fully eccentric core-
annular configuration where the wetting liquid forms the annular phase. >>1, the stratified configuration approaches a fully eccentric core-
annular configuration where the wetting liquid forms the annular phase.
Indeed, the occurrence of annular flow in liquid-liquid systems is more frequently
encountered in oil-water systems of low density differential and small diameter tubes. These
systems are characterized by a large nondimensional Esötviös  >>1 number. In such systems, an
annulus of the wetting phase (surrounding a core of the non-wetting phase) is a natural
configuration which complies with surface tension forces and wall-adhesion forces. Flow patterns
typical to systems of >>1 number. In such systems, an
annulus of the wetting phase (surrounding a core of the non-wetting phase) is a natural
configuration which complies with surface tension forces and wall-adhesion forces. Flow patterns
typical to systems of  >>1 resemble the flow patterns observed in 'microgravity' gas-liquid
systems and include mainly annular flows (wetting phase in the annulus) large bubbles, plugs and
slugs of the non-wetting phase and dispersed flow (continuous oil or continuous water). In such
systems, wettability of the liquids with the tube wall may significantly affect the flow pattern.
Thus, for specified operational conditions, different flow patterns may result by changing the tube
material (hydrophobic or hydrophilic). The start up procedure (oil flowing in the pipe and then
introducing water or vice versa) which affects the effective liquids/wall adhesion, or the entry
condition (type of nozzle used to introduce the two-liquids) are also important factors in
controlling the flow pattern. >>1 resemble the flow patterns observed in 'microgravity' gas-liquid
systems and include mainly annular flows (wetting phase in the annulus) large bubbles, plugs and
slugs of the non-wetting phase and dispersed flow (continuous oil or continuous water). In such
systems, wettability of the liquids with the tube wall may significantly affect the flow pattern.
Thus, for specified operational conditions, different flow patterns may result by changing the tube
material (hydrophobic or hydrophilic). The start up procedure (oil flowing in the pipe and then
introducing water or vice versa) which affects the effective liquids/wall adhesion, or the entry
condition (type of nozzle used to introduce the two-liquids) are also important factors in
controlling the flow pattern.
Stratified configurations with curved interfaces are typical to systems of 0<  <1 , but may
also be realized in systems of low Esötviös number with partial wettability of the fluids
(0< <1 , but may
also be realized in systems of low Esötviös number with partial wettability of the fluids
(0< 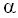 <180o) or due to evolution of hydrodynamic forces which spread one of the fluids over
the tube wall. <180o) or due to evolution of hydrodynamic forces which spread one of the fluids over
the tube wall.
The feasibility of exact analytical solutions for stratified flows is almost restricted to laminar-
laminar flows which are of limited relevance to gas-liquid two phase flows. However, laminar
flow in both phases is frequently encountered in liquid-liquid systems, i.e. viscous oil-water flows.
Analytical solutions for stratified configuration in circular geometry were attempted by Bentwich
(1964) and Yu & Sparrow (1967) and recently, Brauner et al (1995, 1996). The latter provided
analytical expressions in terms of Fourier integrals in the bipolar coordinate system for the two
dimensional velocity profiles and the distribution of shear stresses over the tube wall and free
interface. The interface was considered to be either flat or curved. The interfacial curvature has
been found to have a significant effect on the local and integral two-phase flow characteristics
(Moalem Maron et al, 1995 and Brauner et al, 1997). The prediction of the interface curvature via
energy considerations provides a closure relation required for a complete solution of stratified
flow with curved interfaces. When combined with the solution of the flow equations, the interface
configuration and corresponding flow characteristics can be predicted.
The largest effects of the interfacial curvature on the two-phase flow characteristics are
obtained as the stratified flow configuration approaches either one of the two extremes
corresponding to a fully eccentric core of the lighter phase or the heavier phase. Since the bipolar
coordinates fail to provide a solution in the extreme of fully eccentric core-annular flow, a special
coordinate system has been introduced to solve the flow equations for this configuration. The
determination of the flow characteristics for fully eccentric core flows is of importance as a bound
to evaluate the effect of the core eccentricity in annular flows and the effect of interfacial
curvature in stratified flows.
For practical application, it is necessary to have a model which can also handle turbulant
flows and mixed-flow regimes in the two phases. To this end, the conventional two-fluid model
has been extended to tackle stratified flow with curved interfaces and various flow regimes, in
which case, analytical solutions are complicated and restricted to laminar flows.
The solution of the two-fluid hydrodynamic model can be combined with energy
considerations to yield a complete solution for the interface configuration and the associated flow
characteristics for a variety of two-fluid systems and under variable operational conditions. The
validity of the model and its practical significance for analyzing stratified flows are evaluated in
view of experimental data of the insitu flow configuration and the associated pressure drop in an
oil-water system, recently reported by Valle & Kvandal (1995). The accuracy of the two-fluid
model is evaluated by comparing its predictions for laminar flows with the results of the exact
solution of the Stokes equations for laminar stratified flows with curved interfaces.
The two-fluid model provides a new basis for stability analysis of stratified layers while
accounting for surface tension and wall adhesion forces. The inclusion of interfacial forces, as
additional stabilizing (or destabilizing) terms, may contribute to the understanding of the stability
of the stratified configuration and flow patterns transitions in small diameter two-phase systems,
reduced gravity systems or low density differential systems.
MODELING OF MULTIPHASE DISPERSED SYSTEMS-STATE OF THE ART AND FUTURE DIRECTIONS
Harold R. Jacobs,Phd,P.E.
Professor of Mechanical Engineering
Colorado State University
Fort Collins,Colorado U.S.A.
ABSTRACT
Modeling of multiphase fluid systems where one fluid is dispersed can be
achieved using either Lagrangian-Eulerian formulations or formulations based
on time averaging and volume averaging. Both formulations suffer from lack of
physical based interfacial coefficents for the range of holdup common for many
operating systems. This is particularly true for liquid-liquid systems which are
ideally operated close to the flooding limit for either mass transfer or heat
transfer applications. Herein the state of the art and developments in progress to
provide better tools for interfacial coefficients and to predict drop
agglomeration or breakup are discussed.
SEPARATION OF LIQUID-LIQUID DISPERTIONS
S. Hartland
Department of Chemical Engineering and Industrial Chemistry
Swiss Federal Institute of Technology
Universitätsstrasse 6, 8092 Zürich, Switzerland
Abstract
A model is presented which predicts the variation in the heights of the sedimenting and
coalescing interfaces with time using two parameters namely the initial drop diameter  and coalescence time
and coalescence time  of a single drop at an interface for a given dispersion of known
height Ho, dispersed phase hold-up of a single drop at an interface for a given dispersion of known
height Ho, dispersed phase hold-up  and physical properties. The model predicts the
separation time tf in terms of the initial sedimentation velocity and physical properties. The model predicts the
separation time tf in terms of the initial sedimentation velocity  and maximum
coalescence rate and maximum
coalescence rate  . Figures 1a and 1b show schematically a separating dispersion and the
corresponding sedimentation and coalescence profiles. . Figures 1a and 1b show schematically a separating dispersion and the
corresponding sedimentation and coalescence profiles.

Figure 1. (a) The heights of the sedimenting and coalescing interfaces hs and hc and the dense-packed zone formed at the bottom of a dispersion due to the downward sedimentation of heavier water drops in lighter oil. (b) Schematic variation in hs and hc with time t. The height of the boundary between the sedimentation and dense-packed zones hp is also shown.
Knowing the variation in tf with  , it is possible to generate families of sedimentation
and coalescence profiles corresponding to different initial hold-ups and heights. The
coalescence profiles give the height of coalesced water as a function of time at different
hold-ups. This variation may be replotted in terms of the variation in separated water with
hold-up at different times. Such water cut curves are often determined in the crude oil
industry since crude oil is opaque so the sedimentation cannot be observed and only the
separated water is visible. However, the model equations for the sedimentation and
coalescence profiles may be so expressed to predict the water cut curves and the associated
position of the sedimenting interface. The water cut curves and the families of the
sedimentation and coalescence profiles are thus interchangeable. This is verified using
experimental data for both crude oil and model oil systems. Figure 2 shows the
experimental (symbols) sedimentation and coalescence profiles at different hold-ups for
water dispersed in a viscous crude oil compared with those obtained using the model when
t* hours. Figure 3 shows the corresponding experimental (symbols) variation in
fraction of coalesced water with hold-up at different times compared with that obtained
using the identical model equations. , it is possible to generate families of sedimentation
and coalescence profiles corresponding to different initial hold-ups and heights. The
coalescence profiles give the height of coalesced water as a function of time at different
hold-ups. This variation may be replotted in terms of the variation in separated water with
hold-up at different times. Such water cut curves are often determined in the crude oil
industry since crude oil is opaque so the sedimentation cannot be observed and only the
separated water is visible. However, the model equations for the sedimentation and
coalescence profiles may be so expressed to predict the water cut curves and the associated
position of the sedimenting interface. The water cut curves and the families of the
sedimentation and coalescence profiles are thus interchangeable. This is verified using
experimental data for both crude oil and model oil systems. Figure 2 shows the
experimental (symbols) sedimentation and coalescence profiles at different hold-ups for
water dispersed in a viscous crude oil compared with those obtained using the model when
t* hours. Figure 3 shows the corresponding experimental (symbols) variation in
fraction of coalesced water with hold-up at different times compared with that obtained
using the identical model equations.

Figure 2. Experimental (symbols) sedimentation and coalescence profiles at different hold-ups for water dispersed in a viscous crude oil compared with those obtained using the model (full lines) when t* hours. The broken line shows the locus of the separation time 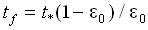 with hold-up with hold-up  . .

Figure 3. Experimental (symbols) variation in fraction of coalesced water hc / Ho with hold-up  at times t= 0.5 to 3.5 hours in increments of 0.5 hours compared with that obtained using the model. The broken line shows the locus of hci / Ho with at times t= 0.5 to 3.5 hours in increments of 0.5 hours compared with that obtained using the model. The broken line shows the locus of hci / Ho with  . .
The variation in hold-up within the batch dispersion with time and position is measured
using an array of  - rays shown in Figure 4 to follow the sedimentation of drops in the
opaque crude oil. The sedimentation profile is obtained from these results with the help of
the Kynch theory. Figure 5 shows the experimental (symbols) variation in hold-up - rays shown in Figure 4 to follow the sedimentation of drops in the
opaque crude oil. The sedimentation profile is obtained from these results with the help of
the Kynch theory. Figure 5 shows the experimental (symbols) variation in hold-up  with
height h within the dispersion at different values of time t for water dispersed in a viscous
crude oil in the presence of a demulsifier when the initial hold-up with
height h within the dispersion at different values of time t for water dispersed in a viscous
crude oil in the presence of a demulsifier when the initial hold-up  = 0.6. The variation
predicted by the model using the values of = 0.6. The variation
predicted by the model using the values of  = 0.894 mm/s, = 0.894 mm/s,  = 0.38 mm/s and ti=
153 s is shown by the full lines. Figure 6 shows the sedimentation and coalescence profiles and
the characteristic lines of constant hold-up predicted by the Kynch theory. = 0.38 mm/s and ti=
153 s is shown by the full lines. Figure 6 shows the sedimentation and coalescence profiles and
the characteristic lines of constant hold-up predicted by the Kynch theory.

Figure 4. Schematic diagram showing a position sensitive  - ray density meter and a sedimenting dispersion. - ray density meter and a sedimenting dispersion.

Figure 5. Experimental (symbols) and simulated (full lines) hold-up profiles at times t= 45 s to 225 s in increments of 30 s for water dispersed in a viscous crude oil in the presence of a demulsifier when the initial hold-up  = 0.6. = 0.6.

Figure 6. Experimental (symbols) and simulated (full lines) sedimentation and coalescence profiles for water dispersed in a viscous crude oil in the presence of a demulsifier when the initial hold-up  = 0.6. The simulated characteristic lines of constant hold-up are also shown. = 0.6. The simulated characteristic lines of constant hold-up are also shown.
SIMULTANEOUS SOLUTION OF STABILITY, PERMEABILITY, AND SWELLING PROBLEMS IN EMULSION LIQUID MEMBRANES BY NON-NEWTONIAN CONVERSION
A.H.P. Skelland
Professor of Chemical Engineering
The Georgia Institute of Technology, USA
ABSTRACT
Our recent experiments have proved the effectiveness of non-Newtonian conversion of
the membrane in emulsion liquid membrane separation processes, with regard to
simultaneously enhanced stability, retained - or improved - permeability, and reduced
swelling. These findings for Type 1 (non-carrier) systems are now extended here to two
new solutes with a variety of membrane formulations to demonstrate the generality of
this approach. There are grounds for optimism in the proposed extension of this new
procedure to Type 2 (carrier-containing) membranes, despite their unique stability
problems.
LIQUID-LIQUID MOTION IN POROUS AND FRACTURED MEDIA
Wouter ZIJL
Netherlands Institute of Applied Geoscience TNO
P.O. Box 6012, NL-2600 JA Delft, The Netherlands
A two-phase liquid-liquid system is generally defined as a system in which two
immiscible liquids, for instance water and oil, flow together and have a shared
interface. When the two liquids flow through the pores and fractures in the subsurface
rock, we deal with two-phase liquid-liquid systems in porous and fractured media.
Such liquid-liquid flow systems are studied for applications in petroleum reservoir
engineering and hydrocarbon exploration, and more and more for applications in soil
and aquifer remediation techniques in the context of environmental engineering.
However, the concept of liquid-liquid systems can be generalised by considering only
one liquid, for instance water, and to consider the water in the pores of the blocks of
intact rock as one phase—the 'rockwater' phase—and the water in the fractures as the
other phase—the 'fracturewater' phase. The distinction between the phases
'rockwater' and 'fracturewater' can further be justified by the fact that the rockwater
entrapped in the almost impermeable rock, has a chemical composition with
concentrations of dissolved matter that differ from the composition and concentrations
in the relatively fast moving fracturewater. Such types of miscible liquid-liquid flow
systems are studied in the context of groundwater flow and transport of dissolved
matter in porous and fractured rock. Liquid-liquid flow and transport in heterogeneous
porous and fractured natural media can be studied from the point of view of many
spatio-temporal scales. The microscopic spatial scale is the scale of the pores and
fractures. On the scale of a block of intact porous rock, the average flow is governed
by Darcy's law. On that scale one of the most prominent parameter for flow is the
permeability of the intact rock. For flow on the scale of a naturally fractured rock
reservoir, the composite permeability is the most dominant parameter describing the
averaged flow through the pores in the intact rock and through the fractures. The
derivation of large-scale composite parameters from fine-scale parameters is generally
called homogenisation or upscaling. Homogenisation is a key item in practical studies
on liquid-liquid two-phase flow systems.
|

