SESSION 5

MASS TRANSFER IN LIQUID-LIQUID SYSTEMS

Chairmen: T. Özbelge, Y.H. Mori

FLOW OF HIGH INTERNAL PHASE RATIO EMULSIONS THROUGH PIPES, ORIFICES AND NOZZLES

Sümer Peker, Tamer Tanilmis, Rifat Özsaygi, Ekrem Tekden
Ege University, Chemical Engineering Department, Bornova, Izmir, Turkey

ABSTRACT. The flow behavior of high internal phase ratio emulsions through pipes of 3.5, 5.6 and 21 mm internal diameters, orifices with D_o / D_i ratios of 0.2, 0.4, 0.6 and 0.8 and nozzles with uniform decrease in diameter is investigated in this work.

1. INTRODUCTION

The use of high internal phase ratio emulsions (HIPRE) with drop volume concentrations greater than 75% in foods, cosmetics and other applications has aroused interest in their complex rheological behavior during the last decade. In high internal phase ratio emulsions, polygonal drop shapes develop with increasing dispersed phase ratios. Formation of a network structure with planar films between the dispersed phase cells leads to the development of yield stresses superimposed on the power law behavior. Thus, Herschel - Bulkley model,

(1)

is generally used to describe the rheological behavior of high internal phase ratio emulsions (HIPRE) under shear. In this work, shear flow of W/O type HIPRE in pipes and elongational flow in nozzles and orifices are addressed.

2. THEORY

For shear flow in pipes the equation of motion was solved for the most general case of 1. power law fluids, 2. presence of a yield stress 3. the presence of slip. The final equation obtained for the average velocity, V, is,

(2)

Elongational viscosity is calculated from the pressure differential due to normal stresses developed under constant extension rate , where the various terms are defined by the equations,

(3)

(4)

Orifice coefficients are calculated from the mechanical energy and total mass balance equations:

(5)

3. EXPERIMENTAL WORK

In the experimental set-up used, pipes of 3.5, 5.6 and 21.6 mm diameters were attached to the bottom of a stainless-steel storage tank through an elbow connection so that the pipes and the orifices would be horizontal. Two nozzles, 30 mm and 20 mm in length were used over which the diameter decreased uniformly from 21 mm to 9 mm. Four different sharp edged orifices with hole diameters ( 4, 8, 12 and 16 mm) corresponding approximately to D_o/D_i ratios of 0.2, 0.4, 0.6 and 0.8, respectively, were used in the experiments. 80, 88 and 94% W/O type emulsions were prepared with 1%(wt) sorbitol solution as the dispersed aqueous phase, paraffinic oil with an empirical formula of C₁₇H₃₆ as the continuous oil phase, polyoxyethylene (2) oleyl ether as the surfactant.

4. RESULTS

The main results for flow in pipes and orifices obtained in this work are plotted in Figures 1 and 2.

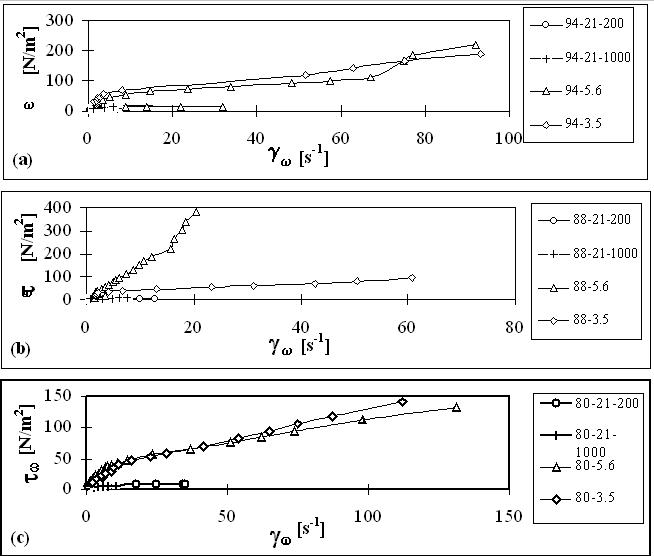
Figure 1. Variation of wall shear stresses with shear rate during the flow of HIPRE
a) 94 % emulsion, b) 88% emulsion, c) 80% emulsion

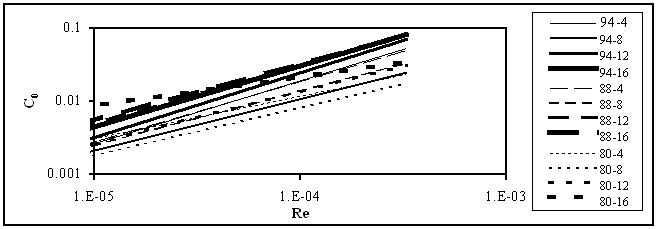
Figure 2. Variation of the orifice coefficients with Reynolds number

5. CONCLUSION

The experimental results obtained in this work confirm the inhomogeneity in the flow behavior of HIPRE. At low velocities restructuring of HIPRE under shear stresses control its flow behavior. At high velocities cell walls rupture to form a film at the walls over which the emulsion flows. Experimental evidence obtained in this work points to the necessity of more work on dynamic behavior of surfactant bilayers for a substantial understanding of the rheological behavior of HIPRE.

PREDICTION OF MUTUAL DIFFUSION COEFFICIENTS OF AROMATICS - BY GROUP CONTRIBUTlON METHOD

X. M. Guo, W. Y. Fei and J. D. Wang
Department of Chemical Engineering, Tsinghua University, Beijing 100084, China

ABSTRACT

The diffusion coeffcient is an essential liquid transport property for the design of liquid-liquid extractors. It becomes more important with the introduction and use of the non-equilibrium stage model recent years, since the accuracy of prediction of the mass transfer coeffcients is the key of the new model application[1,2]. However, experimentally determined diffusion coeffcients (especially for multi-ring hydrocarbons) are scarce and the theoretical approaches to predict liquid diffusion coeffcients are not accurate enough.

The prediction of diffusion coeffcients by group contribution method has been proposed by Ye et al.[3]. According to this new approach, the molecular diffusing area parameters and molecular diffusing activation energy are considered as the factors which influence the molecular diffusion coeffcient. These factors are evaluated by the contribution of the functional groups consisting the molecules in the solution. By fitting a large amount of experimental data of self diffusion and limiting diffusion coeffcients, the diffusing activation energy can be calculated. However, the methods of defining the functional groups and obtaining the group parameters for complex systems (such as multi-ring, hydrocarbons) are unclear and further development is required. Group parameters must be defined for parts of the multi-ring compounds so that this method can be applied to these systems.

For non-polar and non-combined compounds, a certain functional group is considered as a group, such as CH3, CH2 and etc. For high polarity or high combination compounds, such as for DMSO, the whole molecule is considered as a group since the interaction of the molecule is more than the Van Der Waals interaction. For more complex multi-ring hydrocarbon systems, however, the element which combines two rings is considered as a new group, ACC, and the element which combines three rings is considered as another new group, AACC. Naphthalene, for example, can be considered as 8ACH, 2ACC, while pyrene considered as 10ACH, 4ACC, 2AACC.

The diffusion coeffcients at infinite dilution of alkane--aromatic hydrocarbon systems, such as n-heptane--cumene(p-xylene, alpha-methyl naphthalene), dodecane--naphthalene( phenanthrene, pyrene), were measured and the group contribution parameters were evaluated in this paper . Experimental data from references[5-8] were also utilized. The non-linearity Powell method was used to fit the diffusing activation energies and diffusing area parameters. The evaluated results are shown in Tables.

The chemicals used in the study had the following purity as reported by their manufactures: toluene(>99.5%), cumene(>99.9%), p-xylene(>99.0%), alphy-methyl naphthalene(>99.5%), naphthalene(>99.5%), phenanthrene(>99.5%), pyrene(>99.5%). Water used in the experiment was distilled water. A modified version of diaphragm cell technique[8] was used for measuring the mutual diffusion coeffcients. A nickle alloy film with 35mm diameter was used and the details of the apparatus have been described elsewhere[10]. The sample solution was analyzed by DMA60 vibration densimeter.

In order to test our apparatus, the diffusion coeffcients of toluene--DMSO system were measured and compared with literature values[6]. The good agreement between our data and the literature ones demonstrates that our experimental result is reliable and accurate. The experimental diffusivities of selected aromatics in DMSO at different concentration ranges are shown in Figures. The UNIFAC model is used to evaluate the thermodynamic factor. The interaction parameter of UNIFAC model can be obtained by fitting the LLE data respectively for the systems such as toluene ( or naphthalene, alpha-methyl-naphthalene, phenanthrene, pyrene etc.)--DMSO[11]. For cumene--DMSO systems, the parameters are obtained from literature[12].

The diffusion coefficients of cumene( and alph-methyl naphthalene)--DMSO do not change dramatically in the medium concentration range. It is found that the thermodynamic factor changes slowly with the concentration of DMSO for the two systems in the same medium concentration range. This indicates that the effect of concentration on the diffusion coeffcient is determined by the thermodynamic factor primarily if the difference of the viscosity of compounds in the solution is small.

The effect of temperature and DMSO concentration on the diffusion coefficients of naphthalene, phenanthrene, pyrene with DMSO at high DMSO concentration range were discussed respectively. Furthermore, it is clear from the comparison of the diffusion coefficients of aromatic hydrocarbons with different number at cyclic groups (such as toluene, naphthalene, phenanthrene, pyrene) that their diffusion coefficients in DMSO decrease with the numbers of cyclic aromatic hydrocarbon groups and the increasing of length of the branched chain. This may be caused by the molecular space structure and the viscosity of the compounds.

In order to verify the effect of the thermodynamic factor on the diffusion coefficient, the predicted results which evaluated from different interaction parameters of UNIFAC model in the literature were compared with the experimental ones. It is obvious that the deviations are large when the parameter values from the literature[12] were used to calculate the thermodynamic factor. It can be concluded that the thermodynamic factor has a significant effect on the diffusion coefficients for these nonideal systems. It also indicates that a large deviation will occur if the interaction parameters of UNIFAC model obtained from the experimental data of monocyclic aromatic hydrocarbons are directly used to predict the behaviors of polycyclic aromatic hydrocarbons.

It is concluded from this paper:

1. The group contribution method for the prediction of diffusion coeffcients in liquids has been revised. A method of defining the functional groups has been suggested and the group parameter values have been evaluated.
2. The concentration dependence of mutual diffusion coefficients has been determined for DMSO--aromatics( toluene, cumene, p-xylene, naphthalene, alpha-methyl naphthalene, phenanthrene and pyrene) systems at 25 ^oC, using the metallic diaphragm cell technique.
3. The predicted diffusion coeffcients have been found to agree well with experimental data over a wide range of concentration and the major variation in the diffusion coefficient is shown to be due to the thermodynamic factor.

ACKNOWLEDGMENT

The State Key Laboratory of Chemical Engineering, China which supports this research is greatly acknowledged. We are also very grateful to Prof. P. S. Ma, Tianjin University for his helpful advice and discussions.

REFERENCES

1. krishnamurthy, R., Talor, R., AIChE J., 31(3),449(1985)
2. krishnamurthy, R., Talor, R., Ind. Eng. Chem. Pro. Des. Dev., 24(3),513(1985)
3. Ye M., Ph D. Thesis, Tsinghua University, Beijing, 1988
4. Ye, M., Fei, W. Y.,Dai,Y., Wang, J. D., Proceeding of ISEC'96, Vol.1,69, Univ. Of Melbourne, Australia(1996)
5. Sanini, S.A. and Hutchison, P., J. Chem. Eng. Data,18,317 (1973)
6. Thiel, P., Paschke, A. and Winkelman J., Ber. Bunsen-Ges. Phys. Chem., 96(6), 750 (1992)
7. Dymond, J. H. , J. Phys. Chem., 85, 3291 (1981)
8. Johnston, R.C., Lobdell, C.O. and Janauer, G.E., J. Phys. Chem., 83, 1816 (1979)
9. Robinsn, R. L., Edmister, W. C. and Dullien, F.L., J. Phys. Chem., 69,258(1965)
10. Yuan J., Ph.D. Thesis, Tianjin Unuversity, Tianjin,1986
11. Cai Y., Bachelor Thesis, Tsinghua University, Beijing,1995
12. Magnussen T., Rasmussen P. and Fredenslund A., Ind. Eng. Chem. Pro. Des. Dev., 20,331 (1981)
13. Hayduk, W., Laudie, H. AIChE J. 20,611 (1974)

LYSOZYME EXTRACTION BY AOT REVERSED MICELLAR SYSTEMS USING A ROTATING DISC CONTACTOR - SIMULATION OF MASS TRANSFER PERFORMANCE

Jihong Tong^1,* , Sosaku Ichikawa², Shintaro Furusaki^1
1 Graduate School of Engineering, The University of Tokyo, 7-3-1 Hongo,
Bunkyo-ku, Tokyo 113, Japan
² National Food Research Institute, Ministry of Agriculture, Forestry and Fisheries,
2-1-2 Kannondai, Tsukuba, Ibaraki 305, Japan

ABSTRACT

The mass transfer performance of lysozyme using AOT (di-2-ethylhexyl sodium sulfosuccinate) reversed micellar systems formed in isooctane, kerosene and silicone oil was investigated in a rotating disc contactor (RDC) of 38 mm diameter.

The appropriate operating conditions of lysozyme extraction in RDC for the three reversed micellar systems were determined by preliminary experiments. The all experimental runs of lysozyme extraction in RDC were carried out under room temperature. The concentration of AOT in organic phase was maintained at 0.05 M in all experiments. The aqueous phase (0.2M KCl, buffer solution, pH = 8.0) with lysozyme was used as the continuous phase, and the reversed micellar organic phase was the dispersed phase. The two phases flowed countercurrently in the RDC. Lysozyme transferred from the continuous to dispersed phase. The lysozyme concentration profiles along the RDC were measured by taking and analyzing two phase samples, respectively.

The diffusion model was used to simulate the extraction performance. The model was solved numerically by changing parameters to fit the calculated two phase concentration profiles with the meásured profiles using the Complex optimizing method. The axial dispersion coefficients of two phases and the overall mass transfer coefficients based on the continuous phase in the RDC were determined as parameters.

Also, the axial dispersion coefficients and the overall mass transfer coefficients were predicted by using previous correlations. Under the experimental conditions of this study, it was assumed that the mass transfer process of lysozyme extraction by reversed micellar systems was controlled by the diffusion of the protein in the aqueous phase boundary layer. The interfacial resistance was not important in the protein extraction process. It was also assumed that the reversed micellar dispersed droplets were stagnant spheres because of the present of surfactant. The overall mass transfer coefficients of lysozyme from the aqueous phase to the reversed micellar dispersed phase were calculated by combination of some previous correlations under these assumptions. The predicted results were compared with those obtained from the diffusion model solution. The values of mass transfer coefficients obtained from the diffusion model agreed with those by the previous correlations in the literatures fairly well.

It is suggested that the diffusion model may be used for the mass transfer prediction and the column design for the reversed micellar extraction of proteins.

^* Jihong Tong is now working in Soken Chemical & Engineering Co., Ltd., Japan