|
POSTER SESSION 2
NUMERICAL STUDY OF REACTIVE GAS FLOW DURING VENTING PROCESS
Andrei M. Bartenev* , Sergei P. Medvedev*, and Boris E. Gelfand*.
* Institute of Chemical Physics, RAS, 117977, Kosygina str.4, Moscow, Russia
Introduction
The general goal of the present work is to give an interpretation of a complex reactive gas flow phenomena occurring in the course of venting process. As shown in experiments1-3 , the venting of partially burned C3H6O-4O2-3.3N2 and 2H2-O2-2N2 mixtures from a vessel through a short attached duct may result in the secondary explosion and the detonation wave formation. Moreover, the detonation wave propagates inside reaction vessel, thus counter-current process takes place. High - speed photo-records showed, that the local explosion is initiated nearby side-wall of initial run of attached duct. Therefore, abnormal behaviour can not be attributed to a conventional mechanism of DDT in long tubes.
Formulation
The problem was solved on the basis of numerical solution of 2D gasdynamics conservation equations. A chemical energy release according simplified Arrenius law was implemented in the model. Solution scheme used is a modernised Lax-Wendroff method with implemented Flux-Corrected Transport equations for shock capturing. Solution procedure involves splitting scheme.
Two variants of calculation were performed: for long attachment, and for a short attachment tube, which are initially separated from reaction vessel by a diaphragm (membrane). After partial burnout of a combustible gas mixture inside the vessel, the pressure increases and diaphragm is breaking, so the burning mixture is allowed to escape trough attachment tube into the open air. Computation zone was 0.5 x 0.5 m and the mesh used is 150 x 150 cells in each direction. Initial parameters were chosen to match experimental conditions1-3.
Only convective flame front transfer was considered. This assumption is valid if we assume, that flame velocity is small in comparison with sound speed, and small - scale turbulence was neglected. Thus, only ignition of a part of gas mixture which remains unburned prior the beginning of venting process is considered. During the venting, the combustion products can penetrate into the unburned mixture with the formation of large - scale hot pockets.
Calculation results
Short attachment
In the case of short attachment, after initial membrane rupture a shock wave is generated, which been transmitted into outer space takes a typical spherical form. A large - scale vortex is formed nearby the inner edge of attachment During further development of the flow a part of combustion products breaks away with the formation of a large-scale turbulent jet. The temperature in unburned mixture falls gradually and in spite of some pressure fluctuations no explosion was observed. Although, there still exists a possibility to force combustion process due to turbulent mixing, but it appears to be no reason to get a detonation in this case.
Long attachment
Completely another situation occurs in the case of long attachment. The calculations were done at the same initial conditions, but with longer duct. Initial stage of flowfield is the same as in the case of short attachment. However, in the case under consideration the large - scale vortex faced to tube walls. The interaction between vortex and boundaries gives rise to a formation of a region with elevated temperature in unburned mixture. This process is strongly promoted by pressure waves generated from the space occupied by combustion products. It worth to be noted here, that testing calculations without zone of elevated sound speed showed, that temperature at the position of vortex - wall interaction becomes essentially lower and ignition never occurs. Therefore, the presence of combustion products inside the volume at the moment of diaphragm rupture is a necessary condition for the phenomenon under investigation.
Finally, the temperature attains selfignition limit and primary explosion takes place inside the duct. After that, a spontaneous flame 4 propagates through non-reacted mixture inside the storage vessel. During the propagation the flame develops into detonation wave.
Conclusions
In spite of rather simplified treating of the flame in the model, presented analysis qualitatively describes specific features of the phenomenon, marked in the experiments.
Initiating of upstream - directed detonation is conditioned by local explosion at elevated temperature zone formed by the interaction between vortex and duct wall. The position of initiating point depends on the length of attached duct. In the case of too short duct no detonation occurs.
Existing of a region with elevated sound speed inside venting chamber is the necessary condition for obtaining the effect.
To get a quantitative agreement with experiments the model needs an introducing of detailed chemistry kinetics and mechanism of small - scale turbulence.
References
- Medvedev S.P., Polenov A.N., Khomik S.V., and Gelfand B.E., Initiation of upstream - directed detonation induced by the venting of gaseous explosion, Proceedings of 25th Symposium (International) on Combustion, The Combustion Institute, Pittsburgh, 1994, pp.73-78.
- Medvedev S.P., Polenov A.N., and Gelfand B.E., On the experimental evidence for spontaneous detonation onset, Proceedings of the Zel'dovich Memorial, Combustion, Detonation, Shock waves. Semenov Institute of Chemical Physics, Moscow, 1994, vol.2, pp.365-369.
- Medvedev S.P., Polenov A.N., Khomik S.V., and Gelfand B.E., Examination of factors responsible for spontaneous detonation onset in hydrogen-oxygen-nitrogen mixtures, Proceedings of 15th ICDERS, University of Colorado, Boulder, 1995, pp. 183- 186.
- Clarke J.F., Fast flames, waves and detonations, Prog. in Energy and Combustion Science, No.15, pp 241-271, 1989.
LAMINAR FORCED CONVECION HEAT TRANSFER OF A NON-NEWTONIAN FLUID IN ARBITRARY CROSS-SECTIONAL DUCTS
Ibrahim Uzun and Ali Eriţen
Mechanical Engineering Department Kýrýkkale University, 71450 Kýrýkkale,Turkey
Abstract
It is important to develop an understanding of the heat transfer behavior of non-Newtonian fluids in irregular cross-sectional ducts which are commonly encountered in heat exchangers. Numerical solutions for laminar heat transfer of a non-Newtonian fluid in the thermal entrance region for triangular, square, sinusoidal and other type ducts are presented for constant wall temperature. The continuity and parabolic form of the energy and momentum equations in Cartesian coordinates are transformed by elliptic grid generation technique into a new orthogonal coordinates. The boundary of the duct coincides with the coordinate surface. The effects of axial heat conduction, viscous dissipation and thermal energy sources within the fluid were neglected. Then the transformed equations are solved by finite difference technique.
The purpose of this study is to determine the local and mean Nusselt numbers for hyrodinamically fully developed flow of a non-Newtonian power-law fluids in arbitrary cross-sectional ducts. The numerical results show that for each behavior index the Nusselt number at the entry plain decreases from a maximum value to a limiting value when both velocity and temperature profiles are fully developed. As an application of the method, flow and heat transfer results are presented for ducts of triangular, square, sinusoidal, four cusped and square with four indented corners cross-sections. The results are compared with the results of previous works.

Figure 1. The transformation duct geometry from physical(x-y) plain to the computational plain(x-h).
In food, polymer, petrochemical, rubber, paint and biological industries, non-Newtonian fluids are encountered. The investigation of heat transfer problems of non-Newtonian fluids in heating and cooling in heat exchangers will have satisfied economic benefits. The most common heat exchangers employed in these industries are circular and rectangular ducts because of their easy maintenance. The other arbitrarily shaped cross-section ducts are not preferred, because of the difficulty in manufacturing and cleaning. However it is important to have a knowledge of the characteristics of the forced convective heat transfer in steady laminar non-Newtonian flow through arbitrarily shaped cross-section ducts in order to exercise a proper control over the performance of the heat exchanger and to economise the process. There is less research on laminar non-Newtonian fluid flow through irregular than regular boundary ducts, because of the difficulty in describing non-Newtonian fluid behavior in irregular boundary ducts. Although works on non-Newtonian fluid flow in circular, rectangular, triangular, trapezoidal and pentagonal ducts have been found in literature, duct geometries of sinusoidal, four cusped and square with four indented corners have not been found.
In this study steady, fully developed, laminar and purely viscous non-Newtonian fluid flow were studied. Hydrodinamically developed and thermally developing laminar flow was analysed for a non-Newtonian fluid flow through a duct of arbitrary but constant cross-section. The duct configurations and coordinate system are shown in Figure 1. Both the velocity and temperature profiles are assumed to be uniform at the entrance. A computer algorithm was developed for both non-Newtonian and Newtonian fluid flow through in duct geometries mentioned above. However only the numerical results are presented for square, triangular, four cusped duct, rhombic, square with four indented corners and sinusoidal duct geometries.
Numerical solution technique takes advantage of the marginal ellipticity of the physical problem by neglecting the axial diffusion terms in the equations of momentum and energy. The resulting equations are in parabolic form and therefore a two dimensional computational mesh can be constructed at each cross-section and stacked together to from the three dimensional domain. The strategy for dealing with the arbitrary shape of duct cross-sections consists of transforming the physical domain into a rectangular duct by using a coordinate transformation technique.
For the hydrodinamically developed and thermally developing flow, there is only one nonzero component of velocity (u). The constitutive equations of motion reduce to a single nonlinear partial differential equation of the form
 (1) (1)
where (u) is the velocity component in the flow direction, (p) is pressure and (m) is local viscosity at a point in duct. The power-law model was employed to describe the non-Newtonian behavior of the fluid. Consequently, the expression for the local dimensionless viscosity at a point in the channel is given by
 (2) (2)
with (n) being the power-law index and (m) the consistency factor.
Dimensionless momentum equation in transformed coordinates can be written as
 (3) (3)
The function (S) is a variable viscosity and is given by
 (4) (4)
Energy equation for constant property flow, neglecting axial conduction and viscous dissipation in Cartesian coordinates, is
 (5) (5)
The transformed energy, momentum and continuity equations are solved in a rectangular computational domain using finite difference formulation. The momentum and continuity equations are solved only in transverse directions at first cross-section. The energy equation is linearised by setting the unknown to its value at previous axial step. The indices i, j and k indicate positions in the x, h and z directions respectively. The origin is designated by i=j=k=1 which is bottom left corner of computational plain. The direction grid number** (x, h and Z) of mesh spaces are taken equal to 1/NI, 1/NJ and 1/NK respectively. The dimensionless transverse step sizes, Dx and Dh, are taken equal but axial mesh space DZ was different. The axial step size DZ was taken to be 5x10-5. Starting with this value, subsequent step sizes are gradually increased using the relation DZn+1=(1.1)x(DZn) until DZ>1.0x10-3.
Reliable data for laminar fully developed flow in square and rhombic ducts are available in literature. Several test calculations were carried out in order to verify the performance of the solution procedure. Firstly, the flow of Newtonian fluid was considered, because numerical results are already available in previous studies. The numerical results were presented for comparison. In addition elliptic grid generation technique and numerical solution method are compared also results of other methods. The excellent agreement was found between this work and the others. Due to the geometry concerned in present study, no numerical results was found in the literature for some ducts studied in this work. The results of some channel geometries such as four cusped and square with indented four corners ducts in the literature are also included. Local and mean Nusselt number values, fully developed velocity and temperature profiles have been shown in tables and figures for above duct geometries.
SIMULATION OF MELTING IN A THREE-DIMENSIONAL BODY
H. D. Zughbi1, R. Kahraman1, Y. N. Al-Nassar2, M. A. Hastaoglu3 and N. Sobh4
Departments of 1Chemical and 2Mechanical Engineering, King Fahd University of
Petroleum & Minerals (KFUPM), Dhahran 31261 Saudi Arabia.
3 Department of Energy Systems, Gebze Institute of High Technology, Gebze, Turkey
4 Saudi ARAMCO, Dhahran, Saudi Arabia
Heat transfer with phase change plays an important role in many industrial and natural processes. Such processes include crystal growth, latent heat of fusion in thermal energy storage, purification and casting of metals, plastics manufacturing, transport of liquids and freezing/thawing of ice and soil.
Phase change problems have been the subject of intensive research over the past two decades. The earlier models were in general based on conduction heat transfer, both in the solid and liquid. However the actual physical processes show that natural or forced convection may be present in the liquid and sometimes plays a dominant role. This has also been shown experimentally by many workers. Later models have taken convection into account, however most of those models were two-dimensional and although there have been some three-dimensional models, a survey of the literature shows that those models were for the case of cooling or heating from a vertical wall and noticeably lacked quantitative comparison with experiments.
THEORETICAL BACKGROUND
In a three dimensional object when a certain boundary is subjected to a temperature higher than its melting point liquid starts forming at any portion of the solid if temperatures exceed melting point of the solid. Heat transfer takes place in both phases and the resulting equations have to be solved in each region.
At the solid liquid interface a heat balance results in a differential equation to track the location of the interface. The mode of heat transfer will be conduction in the solid, while in addition to the conduction in the liquid, there could be forced or density induced natural convection. Flow may also be caused by the density difference between the solid and newly forming liquid.
If the liquid forming in melting operation is stratified, then one is concerned only with conduction. However in actual operations liquids are disturbed by external perturbations and frequently liquids are not stratified. In this case the equations of motion have to be considered and the problem becomes significantly more complicated.
Another difficulty is that the boundaries may not be of standard geometrical shape (regular cylinder, sphere or plane). The shape of boundaries and the distribution of boundary conditions may also force the melt front not to have a 'good' geometric shape. Various thermophysical properties may depend on temperature. In such cases a (semi) analytical or approximate solution is not possible and one has to develop numerical schemes.
MATHEMATICAL FORMULATION
For the case without natural convection the equation of conservation of energy in each region is written. The motion of melting front is governed by an energy balance at the interface with the proper initial and boundary conditions applied.
The existence of natural convection complicates the model extensively. The equations of continuity, motion (three components) and energy have to be considered simultaneously.
NUMERICAL SOLUTION TECHNIQUE
Two numerical approaches are used to solve the melting problem. Firstly an own program using finite differencing incorporating certain approximations is used. At grid points adjacent to boundaries, string-intersected approximations to derivatives are used. Now a more rigorous model solving for primitive variables is being developed. Secondly a full three-dimensional and rigorous model is being developed using the general purpose fluid mechanics and heat transfer finite volume package, PHOENICS.
EXPERIMENTAL WORK
Experiments were carried out with ice. Water in a copper container was frozen to - 29oC with several thermocouples imbedded within. The container is a cube of 20 cm a side (xL = yL = zL = 0.2 m).
The ice container was partially or totally immersed in an ice-water bath. The top of the ice was contacted with a hot box with a surface area of 0.1m´ 0.1m (0.01 m2) in some experiments. In other experiments the area of the heating area was reduced by about 12 times to 0.00085 m2 . Hot water at 70 oC is circulated from a reservoir, keeping the hot surface in contact with the top of the ice box at a desired temperature. The thermocouple readings and the depth of the melt front were periodically recorded during the experiments.
RESULTS AND CONCLUSIONS
In the first experiment the ice container was partially immersed (half way up the sides) in an ice-water bath. The top of the ice was contacted with a hot box. The hot area in contact with the top surface was 0.01 m2 In the second and third experiments, the same set-up was also used with the main change being a substantial reduction in the area of the hot box. The hot area in contact with the top surface of the ice box has been reduced to 0.00085m2. The initial ice temperature and the temperature of the hot box are unchanged.
In the second experiment, only the bottom of the ice box was touching an ice-water bath while all the sides were not immersed and were subjected to ambient air. In the third experiment the whole sides of the ice box were immersed in an ice-water bath.
The advance of the melt front with time is shown in Fig. 1 for the three different experiments. Since ice lifts after a certain time, limited values are reported. In fact a small amount of melting near the walls of the container is observed due to the high conductivity of the container walls. From Fig. 1 we can use interpolation to estimate the time required for the ice in the box to melt completely. These times are 12 hours for the case of large hot surface and half immersed, 25 hours for the case of small hot surface and unimmersed and 47 hors for the case of small hot surface and fully immersed.
Fig. 1 shows two distinct rates of melting for each of the three experiments. A high rate of melting was observed up to about 1.5 hours and then a slower rate until the end of experimental runs. The high rate of melting is due to high convective losses to ambient air through the top surface of the ice block.
A numerical model taking into consideration conduction only predicts for the first case a total melting time of about 35 hours which is about three times higher than the actual estimated time.
A numerical model has been developed which takes convection into consideration. Results of this model show good agreement with experiments. Fig. 2 shows that the melt thickness versus time predicted from the model agrees well with the experimental results of the first experiment reported earlier.
Further numerical results will be presented in the paper, especially results from the more rigorous models developed, one using PHOENICS while the other is the in-house model.
Melting in a three dimensional bounded object is being numerically and experimentally studied. Results show a strong effect of convection. Heat losses from the walls of the ice box have a strong effect on the time required for the ice to melt. Results of the in-house simplified numerical model showed good agreement with experimental work.
ACKNOWLEDGMENT
This project has been funded by King Fahd University of Petroleum & Minerals under Project #ME/NUMERICAL/184.
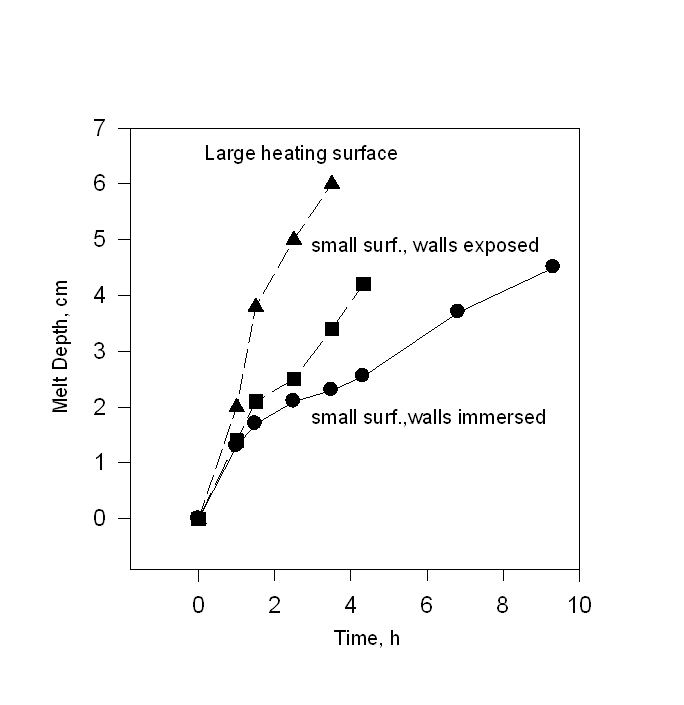
Figure 1: Melt thickness versus time for three different experiments
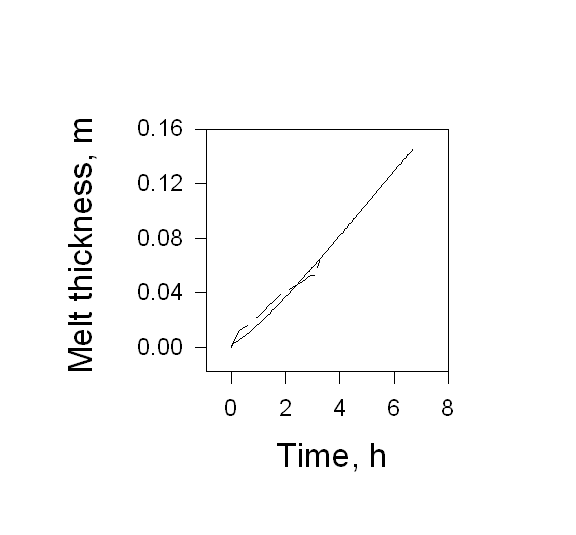
Figure 2: Melt thickness for case 1: experimental (broken line) versus numerical results
FIXED GRID FINITE ELEMENT ANALYSIS OF SOLIDIFICATION
Jerzy Banaszek*, Marek Rebow* and Tomasz A. Kowalewski**
*Institute of Heat Engineering, Warsaw University of Technology, PL 00-665 Warsaw
**Center of Mechanics, IPPT PAN, PL 00-049 Warsaw, Poland
Naturally occurring substances, as well as materials used in engineering applications, almost always exist in the form of a multi-constituent system (e.g. alloys). The presence of a binary component within a material alters the nature of the solid-liquid phase transition. Differences in constituent solubility within each phase cause concentration differences within the mixture, leading to non-equilibrium solid-liquid coexistence, non-discrete phase transition (mushy region) and solutal buoyancy. The ability to predict the behaviour of the binary system during solid-liquid phase change is of formidable value to engineering; and an accurate understanding and control of this phenomenon is critical in the improvement and refinement of many technological processes.
The primary difficulty in analysis of such systems is that the nature of the interface movement, latent energy transfer, species redistribution and convection mechanisms, introduces non-linearity in the governing equations. Therefore, despite a large number of relevant papers published recently, developing numerical algorithms for these complex problems, that are robust, computationally efficient and geometrically versatile, is yet a considerable challenge, particularly in the FEM context.
The first but crucial step is to develop reliable 2-D numerical models and their algorithms addressed to simulate heat, mass and momentum transfer in both isothermal and temperature-range solid-liquid phase change. In this context, this paper presents the FEM algorithm that is based on the semi-implicit operator splitting technique tied with the enthalpy-porosity approach. Its performance is studied by solving some benchmark problems, available in literature, and by comparing obtained results with both the boundary-fitted FDM front tracking solution and experimental data, in the case of pure water solidification.
To include the effect of free convection in the liquid and mushy regions the whole set of coupled momentum, energy and mass balance equations should be solved simultaneously. In order to improve the computational efficiency of such complex and time-consuming calculations the semi-implicit operator splitting algorithm1 has been used. Convection and diffusion are treated separately, i.e.: convective terms of momentum and energy equations are integrated in time using the second order Adams-Bashforth scheme, whereas the diffusive terms are calculated with the backward Euler scheme. Chorin's fractional step method2 has been applied to decouple the continuity and momentum equations. First, the momentum equation with disregarded pressure gradient is solved and then the provisional velocity field, thus obtained, is corrected by taking into account pressure contribution through the enforcement of the incompressibility condition.
In the temperature-range solidification of a binary system three different zones can be distinguished - a solid region, a liquid one and a mushy zone that consists of both these phases. At the liquid/solid interface the liquid velocity should take zero value, whereas in the mushy zone it should gradually decrease with increase of the solid volume fraction. Such behaviour of the velocity field in the vicinity of a sharp or dispersed phase front can be modelled by various switch-off techniques. The most physically justified approach is to assume that a mushy zone can be treated as a porous medium with porosity equal to the liquid volume fraction3. The pressure gradient is described by Carman-Kozeny law and an additional source term is added to the momentum balance equation to imitate the above described behaviour of the system in the mushy zone. In the solidified region the fluid velocity can also be suppressed by the variable viscosity approach4. Both these switch-off techniques have been adapted in the algorithm.
To solve a moving boundary phase change problem on a fixed FEM grid, Voller's general source-based method5 is generalized to calculate convective heat transfer effects. The method accounts for the latent heat evolution through the use of the total enthalpy concept that includes sensible heat and liberated latent heat in one dependent variable.
The proposed algorithm has been verified by solving some available benchmark problems1,4,6 for internal and external viscous incompressible fluid flows as well as for a binary alloy solidification driven by conduction and convection. Solutions obtained are free from wiggles and spurious pressure modes and they fit fairly well to the results reported by others1,4,6.
As an example, the results of calculations of the Al-alloy solidification with convection are given in Fig.1, where streamlines (with their values augmented 105 times) and isothermal lines are shown for the liquid Al-alloy confined in a square cavity (of 0.05m x 0.05m) and cooled from the initial temperature 710oC through the right cold wall, kept at temperature 610oC (the left wall temperature is equal to 610oC. The volumetric liquid fraction is a linear function of temperature in the mushy zone (between 625oC and 650oC) where the fluid viscosity is assumed to be a linear function of temperature.

Fig.1 Streamlines and isotherms for Al-alloy solidification driven by conduction and convection
The robustness of the method makes it preferable for solving practical engineering of complex geometry and fluid properties. However, its freedom within methodology for the definition of phase change region properties becomes a drawback, when its accuracy is of demand. To elucidate limitations of the method detailed comparison is performed with the experimental7 and numerical data8 for freezing of water in the differentially heated square cavity. The temperature of the cold and hot wall is set to -10oC and +10oC, respectively. The experimental data consists of the interface growth rate, the velocity and temperature fields collected for several time steps in the vertical plane of symmetry of the cube7. The reference numerical data have been generated using 3-D finite-difference code ICE3D written by CFD Group at NSW University8. The boundary-fitted computational approach used in this code allows physically relevant description of the phase change front propagation. In the computations a very small time step is chosen to ensure smooth transition of the generated grid and the overall stability of the numerical calculations of the transport process. Freezing of water, unlike other natural-convection dominated phase change problems, is distinct due to the presence of density anomaly. Nonlinear variation of density with temperature with its maximum at 4oC, creates a potential source of errors, when comparing physical and numerical experiments. Hence, the numerical tests have been generated both for hypothetical "Boussinesq water" as well as for the variable properties water, to compare with the proposed algorithm. The reliability of the proposed fixed grid FEM model appears to be ``operationally'' acceptable for solving single component phase change problems, providing the sufficiently dense grid is used. The next necessary step is an experimental validation of the mushy region model for the binary solutions (freezing of salt water) to provide reliable data for a comprehensive accuracy analysis of the proposed FEM algorithm.
ACKNOWLEDGMENT
This work is supported by the National Committee for Scientific Research ( the grant entitled: Experimental and Numerical Analysis of Free Convection and Phase Change Transitions in Binary Systems)
REFERENCES
- B. Ramaswamy, T.C. Jue and J. E. Akin: Semi-Implicit and Explicit Finite Element Schemes for Coupled Fluid/Thermal Problems. Int. J. Num. Meth. Eng. vol. 34, pp.675-692, 1992.
- J. Chorin: Numerical Solution of Navier-Stokes Equations. Math. Comp. vol. 22, pp.745-762, 1968.
- A.D. Brent and V.R. Voller: Enthalpy-Porosity Technique for Modelling Convection-Diffusion Phase Change: Application to the Melting of a Pure Metal., Numerical Heat Transfer, vol.13, pp.297-318, 1988.
- A.S. Usmani, R.W. Lewis and K.N. Seetharamu: Finite Element Modelling of Natural Convect-ion - Controlled Change Phase. Int. J. Num. Meth. in Fluids, vol.14, pp.1019-1036, 1992.
- V.R. Voller and C. R. Swaminathan: General Source-Based Method for Solidification Phase Change. Numerical Heat Transfer, Part B, vol.19, pp.175-189, 1991.
- C.R. Swaminathan and V.R. Voller: General Enthalpy Method for Modelling Solidification Processes. Metallurgical Transactions, vol.23B, pp.651-664, 1992.
- T. A. Kowalewski, M. Rebow: An experimental benchmark for freezing water in the cubic cavity, Proceedings of ISACHT'97, Turkey, 1997.
- G. H.Yeoh, M. Behnia, G. de Vahl Davis and E. Leonardi: A numerical study of three-dimen-sional natural convection during freezing of water, Int. J. Num. Meth. Eng. vol. 30, 899-914, 1990. Also: G.H. Yeoh: Natural convection in a solidifying liquid, Ph.D. Thesis, University of New South Wales, Sydney 1993.
THE SPEED OF THE PHASE BOUNDARY BY MODEL KINETIC AND HYDRODYNAMIC EQUATIONS OF VAN DER WAALS FLUIDS
Kazimierz Piechór and Bogdan KaŸmierczak
Institute of Fundamental Technological Research
ul. Œwiêtokrzyska 21, 00-049 Warszawa , Poland
e-mail:kpiechor@ippt.gov.pl, bkazmier@ippt.gov.pl
Introduction
In the case of fluids whose pressure is not a convex function of the specific volume, what occurs in so called retrograde fluids, the unsteady Euler equations are strictly hyperbolic, but the sound speed is no longer a monotonically increasing function of the fluid density. This fact gives rise to many spectacular phenomena: the entropy grows across the shock but the pressure, for instance, can decrease rather than increase , so the shock is expansive Next, shock waves of finite, nonzero intensity can move at the speed equal to either the upstream or downstream speed of sound.
The classical shock admissibility criteria are insufficient to single out the physically relevant solution, and the numerical schemes developed for ideal gases are inapplicable to such problems. To overcome the first difficulty so called Oleinik-Liu extended entropy condition were introduced, but the second question remains essentially open, except the simplest cases.
The problems complicate further if we proceed to study liquid-vapour phase transitions. In this case, for some values of the specific volume and the temperature, the Euler equations change type from hyperbolic to elliptic. Physically, this means that the sound speed ceases to exist in such regions. Consequently, the Hugoniot curves become disconnected or form loops. Hence, even the Oleinik- Liu conditions need an extension or replacement. Also, new types of waves occur. They are subsonic with respect to the states on both sides of the discontinuity. Such waves are called the phase boundaries.
One of the natural ideas of determination of new shock admissibility criteria is to use an augmented physical theory. It would seem that it is most natural to use the dissipative Navier-Stokes equations. However, it turns out that they do not admit any extension of the Oleinik-Liu conditions, and they rule out continuous solutions to phase boundaries.
That is why, it was proposed to use so called equations of capillarity. The basic idea of this theory is that the internal energy depends not only on the density and temperature but also on their space gradients. This results in raising the order of the fluid dynamics equations: the capillarity equations are of the third order whereas those of Navier-Stokes are of the second. Within this theory, even the problem of existence of phase boundaries becomes very difficult, and its solution needs subtle tools of algebraic topology. It turns out that if the wave exists, given the left state, it does for one special speed only. Hence, this speed becomes an additional unknown. Numerically, the equations are stiff and unstable, so the numerical results are very limited.
However, this is not an end of our troubles, because the equations discussed above are of the phenomenological thermodynamics origin. As it is known, at least as fluids are concerned, such a theory cannot describe correctly the flow in the regions where the gradients are very large. In particular it refers to the shock waves and phase boundaries. Thus, the use of kinetic theory is inevitable.
The model and results
The aim of the paper is to present the simplest, but far from being trivial, example of a kinetic approach to the problem of phase changes, and some of the results. Our idea consists in the use of one kinetic equation both to the liquid and the gaseous phase. However, if one proceeds to realise such a project then one faces a very fundamental question: simply, there is no universal and fully satisfactory kinetic equation suited to liquid dynamics and phase transition . Therefore, it is necessary to decide upon one out of not very many models. We have chosen the so called Enskog-Vlasov equation.
Unfortunately, this equation is too complicated to be used for determination of any nontrivial flow. That is why we have elaborated its discrete velocity models and obtained a more tractable system of integro-differential equations. To simplify them we are forced to take additional assumptions. We define in a suitable way the Knudsen number and expand those terms of the equations, which represent the hard-core collisions the attractive tail, in a power series. As the result we obtain a system of purely differential equations. We limit our considerations to one-dimensional unsteady flows. Then some symmetry properties allow us to reduce our system to three non-linear partial differential equations. Using the Chapman-Enskog asymptotic procedure we deduce model Euler, Navier-Stokes, and capillarity equations.
These simplified equations will be used to demonstrate the afore-said basic problems of the theory of van der Waals fluids. In particular, graphs exposing the influence of the change of type of the Euler equations on the Hugoniot loci and the wave speed will be presented. In addition to so called impending shock splitting will be analysed and numeric results showing that this effect is damped by the increase of the intensity of the capillarity terms will be presented.
Finally, we discuss the problem of phase transitions. First of all, we show that the model kinetic equations and the capillarity approximation to them provide the same Maxwell equal area rule for equilibrium phase transitions. The key result of our paper concerns the most important, from the physical point of view, case of phase boundaries whose speed is close to zero. By means of the Implicit Function Theorem we deduce, both from the model kinetic equations and from the capillarity approximation to them, explicit formulae for the mobility of phase boundaries. These formulae are different. This means that the kinetic and phenomenological approaches can provide different descriptions of condensation/evaporation transitions.
Unfortunately, the numerical evaluation of the structures of the phase boundaries is extremely difficult because of the strong instabilities involved in the problem of saddle-saddle connections and remains open.
NUMERICAL SIMULATION OF CRYSTAL GROWTH BY FLOATING ZONE METHOD
Artemyev V.K.*, Ginkin V.P.*, Gusev N.V.*, Luhanova T.M.,
Ozernyh I.L.**, Shishulin V.P.*, Sviridenko I.P.*
* State Scientific Centre of Russian Federation, Institute of Physics and Power Engineering,
Bondarenko sq. 1, Obninsk, Kaluga region, Russia, 249020
** Scientific Investigating Centre of Cosmic System Technique,
Koroleva 6, Obninsk, Kaluga region, Russia, 249020
Currently, a series of experiments on crystal growth by the floating zone1-2 method has been conducted on the board of the FOTON satellite and on the board of the MIR space station. The ZONE-4 facilities were used for this purpose. As a result, crystals of germanium, indium antimonide, gallium antimonide 15-20 mm in diameter and 60 mm in length have been produced. The technological experiment is implemented in the following manner: a bar with 15-20 mm in diameter and 110 mm in length is set into a 30 mm quartz ampoule; the specimen is held inside the ampoule by means of 60mm long graphite inserts of complicated shape. The specimen is heated up until a melt-down zone is formed and kept for some time. After that, the ampoule starts to travel with a certain velocity relative to the heater.
The space conditions substantially extend the capabilities of the floating zone method, because the surface tension forces allow a melted zone of much bigger diameter than that under terrestrial conditions. When testing under terrestrial conditions, an additional quartz tube is used to retain the melt, what can lead to some change in the heat flux to the specimen. Besides, the mechanisms inducing the development of convective flows are substantially different: in terrestrial conditions, the thermal gravitational convection prevails, whereas in microgravity so do the Marangoni convection. In view of this, detailed theoretical and numerical studies of heat and mass transfer processes are needed. The present report considers the problems of numerical simulation of melting and crystallization processes and presents some calculation results and their analysis.
The Stephen problem is solved with taking account of the effect of convective heat exchange in the melted zone. In general statement, the continuity and momentum equations in unitless form read:
 , ,
where  is the velocity vector, p is the pressure, is the velocity vector, p is the pressure,  is the Grashof number, b is the coefficient of thermal expansion, and is the Grashof number, b is the coefficient of thermal expansion, and  is the acceleration vector. is the acceleration vector.
The heat transfer equation reads

and the condition on the moving interfacial boundary:

where h is the enthalpy; r is the density; T - temperature, DT- temperature drop, l - thermal conductivity ; the index "s" refers to a solid phase, "l" - to a liquid phase, "f"- to the interfacial boundary; cf- latent heat of fusion, Vf- a rate of interface motion, Pr is the Prandtle number, Re is the Reynolds number; n - is the unit vector normal to the solid/ liquid interface. An explicit dependence of all material properties upon enthalpy is taken into account.
'The Dirichlet-Voronoi nodalization, which is used for yielding discrete analog of interior of zones, gives an irregular finite-difference mesh in this problem. For space approximation, the method of control volumes is employed, and for the time approximation - the implicit Euler scheme. As a result, a conservative and stable difference scheme is obtained. By the form of representation, the equation for cells containing single-phase material do not differs from those for cells where the phase transition occurs. However, when interpreting the results of calculations, one should have in mind the following essential difference: in two-phase cells the discontinuous function of enthalpy is averaged.
When deriving the discrete form of radiate heat exchange equations, all boundary components adjoining the same cavity are reduced to a single vector. The resulting heat fluxes are expressed in terms of boundary components temperatures using a slope matrix.
In combining the equations for all binding groups of zones and for all binding cavities, we obtain a set of closed non-linear algebraic equations relative to the mean enthalpy values by the cells of the mesh nodalization and mean heat flux values on common boundaries of cells and on the components of the boundary. Let us call this system a global system. The system involves the time spacing t as a parameter, for which the upper restriction resulting from the convergence conditions of the algorithm for the global nonlinear system solution is specified.
The method of the global nonlinear system solution is based on the iterations of boundary components temperature values. The partial system of heat balance equations for one group of zones is solved as follows: first, heat fluxes are eliminated and then the system is linearized by the Newton's method and solved against enthalpy increments by the A*A method of minimal iterations with preconditioning the reference system by the incomplete factorization method. This procedure is described in the paper3 in more detail.
The heat convection equations are considered in Boussinesq approximation. The equations are solved in terms of natural variables by an implicit method applying monotonous balance neutral difference approximations. In the course of the nonstationary-process calculation, heat convection equations are periodically solved using the calculated thickness and melt-down zone shape, obtained from the Stefan problem. After that, heat fluxes, the location and the shape of the interface, melt-down front and crystallization front are corrected.
The developed procedure and program made it possible to numerically analyse the behaviour of the melt-down zone in the process, the effect of heat transfer conditions at the sample ends, the variation of net power in the course of the process, the role of ampoule motion and thermal insulation. As an example, the calculation of the melt-down zone width variation as a function of the heater position with respect to the specimen end is shown on the Fig.1.
REFERENCES
- Barmin, I.V., Egorov, A.V., Senchenkov, A.S., Results of crystal growth experiments by FMZ on zona facilities in microgravity, Proceedings 8th European Symposium on Materials and Fluid Sciences in Microgravity, Brussels, Belgium, 12-16 April 1992, ESA SP-333, pp 591-596.
- Barmin, I.V. and Senchenkov, A.S., Technological equipment of Splav Technical Center for producing material in space. Some results of the experiments on crystal growth, Microgravity Q. Vol. 3.No. 2-4, pp 233-239, 1993.
- Ginkin, V.P., Artemyev, V.K , Gusev, N.V., Zinin, A.I., Ozernyh, I.L., Numerical Simulation of the Process of a Crystal Growth from the Melt, Proceeding of the ISSDT ' 95, Berg-en-Dal, Kruger NationalPark, South Africa, 15-17 November, 1995, pp 228-232.

ANALYSIS OF NATURAL CONVECTION DURING SOLIDIFICATION OF A PURE METAL
M. Giangi, F. Stella
Univ. di Roma "La Sapienza",
Dip. di Meccanica ed Aeronautica,
Via Eudossiana 18, 00184 ROME (Italy)
e-mail: fulvio@stella.ing.uniroma1.it
INTRODUCTION
Heat transfer and thermal oscillations during the solidification phase of metallic or semi-conductor melts are very important for improving the quality of the final product1. As matter of fact the effect of natural convection in the liquid phase is of great relevance for describing growth velocity in the solid and shape of liquid-solid interface. In the past a considerable effort has been direct to mathematical modelling of fluid flow during phase change2,3,4. The mathematical models for the simulation of two phase problems can be classified in singles and multi-domain methods.
A numerical study of solidification of a pure metal conducted on a fixed-grid2 is proposed in the present paper. One of the advantages of the fixed-grid method is that a unique set of equations and boundary conditions is used for the whole domain, including both solid and liquid phase. Computational cells with simultaneous presence of solid and liquid will be treated using the porous medium model, so an extra source term is added into the governing equations. A term of Darcy type has been adopted in the momentum equation as extra term in order to take in account of fluid-solid interaction; latent heat of fusion will be considered as an extra (sink) term in the energy equation in order to properly evaluate the liquid-solid phase change.
This model has been identified as the enthalpy-porosity method3.
Main advantage of the adopted method is that the liquid-solid interface has not to be explicitly tracked. The method takes account of its motion through the changes in the liquid fraction. Relative merits and demerits of single-domain and multi-domain methods have been discussed by R. Viswanath and Y. Jalura4. Numerical tests will be presented for a 2D solidification problem in a square cavity and compared, when possible, with available results.
MATHEMATICAL MODEL
Following the classical mixture theory5 the governing equations are re-written using an averaged quantity called continuum velocity:
 (1) (1)
where  , ,  are the velocity of the liquid and solid phase respectively, are the velocity of the liquid and solid phase respectively,  are the liquid and solid mass fraction. According to the saturated mixture conditions the mass fractions must add to unity: are the liquid and solid mass fraction. According to the saturated mixture conditions the mass fractions must add to unity: . .
Using the  definition (1) the governing equations on a volume that can be both solid and/or liquid results: definition (1) the governing equations on a volume that can be both solid and/or liquid results:
 (2) (2)
 (3) (3)
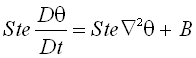 (4) (4)
The liquid phase has been assumed Newtonian and incompressible, Boussinesq approximation is assumed to be valid. The densities in the liquid and in the solid phase are assumed equal and constant.
The Darcy source term in the momentum equation (3) can be identified with reference to the Kozeny-Carman equation for flow in porous media5:
 . .
Where  is a constant dependent on the porous media morphology and is a constant dependent on the porous media morphology and  is a computational small quantity used to avoid division by zero. is a computational small quantity used to avoid division by zero.
As the liquid fraction goes to zero (in the solid phase) the source term, in eq.(3), dominates the equations and forces the velocities to become zero in the solid phase.
In the energy equation (4) the source term 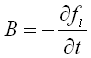 is obtained by writing the entalphy is obtained by writing the entalphy  as as  with with  where where  is the latent heat of fusion. is the latent heat of fusion.
The dimensionless parameters occurring in eq. (2-4) are the Prandtl number  , the Rayleigh number , the Rayleigh number  and the Stefan number and the Stefan number  . .
Where  is the coefficient of thermal expansion, is the coefficient of thermal expansion, the cavity height, the cavity height,  the temperature difference between the hot and cold walls, the temperature difference between the hot and cold walls, 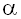 the thermal diffusivity, the thermal diffusivity, 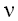 the kinematic viscosity and the kinematic viscosity and  the latent heat of fusion. the latent heat of fusion.
Eq. (2-4) are discretized by using a finite volume method technique on a staggered grid. The numerical solution of the field equations is obtained by using SIMPLE algorithm6. Advancing in time for the momentum equation is performed using an ADI technique, while the elliptic solver for the pressure correction is based on a preconditioner BI-CGStab method7.
TEST PROBLEM
As a test problem solidification of pure gallium in a square cavity (with isothermal side walls and adiabatic top and bottom walls) has been adopted. The left wall is maintained at a temperature  and the right wall at a temperature and the right wall at a temperature  (with (with  phase change temperature). phase change temperature).
Numerical results will be presented for steady state and transient problems.
Numerical results
Numerical study of solidification of pure gallium (Pr=0.0216) with a Stefan number of  has been conducted in a two-dimensional cavity of aspect ratio A=1. has been conducted in a two-dimensional cavity of aspect ratio A=1.
The dimensionless temperature  varies from 0 to 1 between the cold ( varies from 0 to 1 between the cold ( ) and the hot ( ) and the hot ( ) walls and the phase change temperature ) walls and the phase change temperature  . .
The initial condition for the liquid fraction and the temperature are respectively:  and and  . .
In Figure 1 the streamlines and the solid-liquid interface at 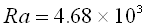 are sketched, showing a large recirculating cell. A uniform are sketched, showing a large recirculating cell. A uniform  mesh has been adopted. mesh has been adopted.
When  is increased the flow becomes oscillatory. At is increased the flow becomes oscillatory. At  an oscillatory flow is found. Streamlines are similar to those of an oscillatory flow is found. Streamlines are similar to those of 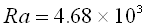 (Fig. 1) and are not reported here. For this solution an (Fig. 1) and are not reported here. For this solution an 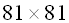 mesh has been adopted. mesh has been adopted.
In order to confirm the oscillatory nature of the flow, comparison results have been obtained in the square cavity without phase change at the same  and and  , founding similar frequencies of oscillation. , founding similar frequencies of oscillation.
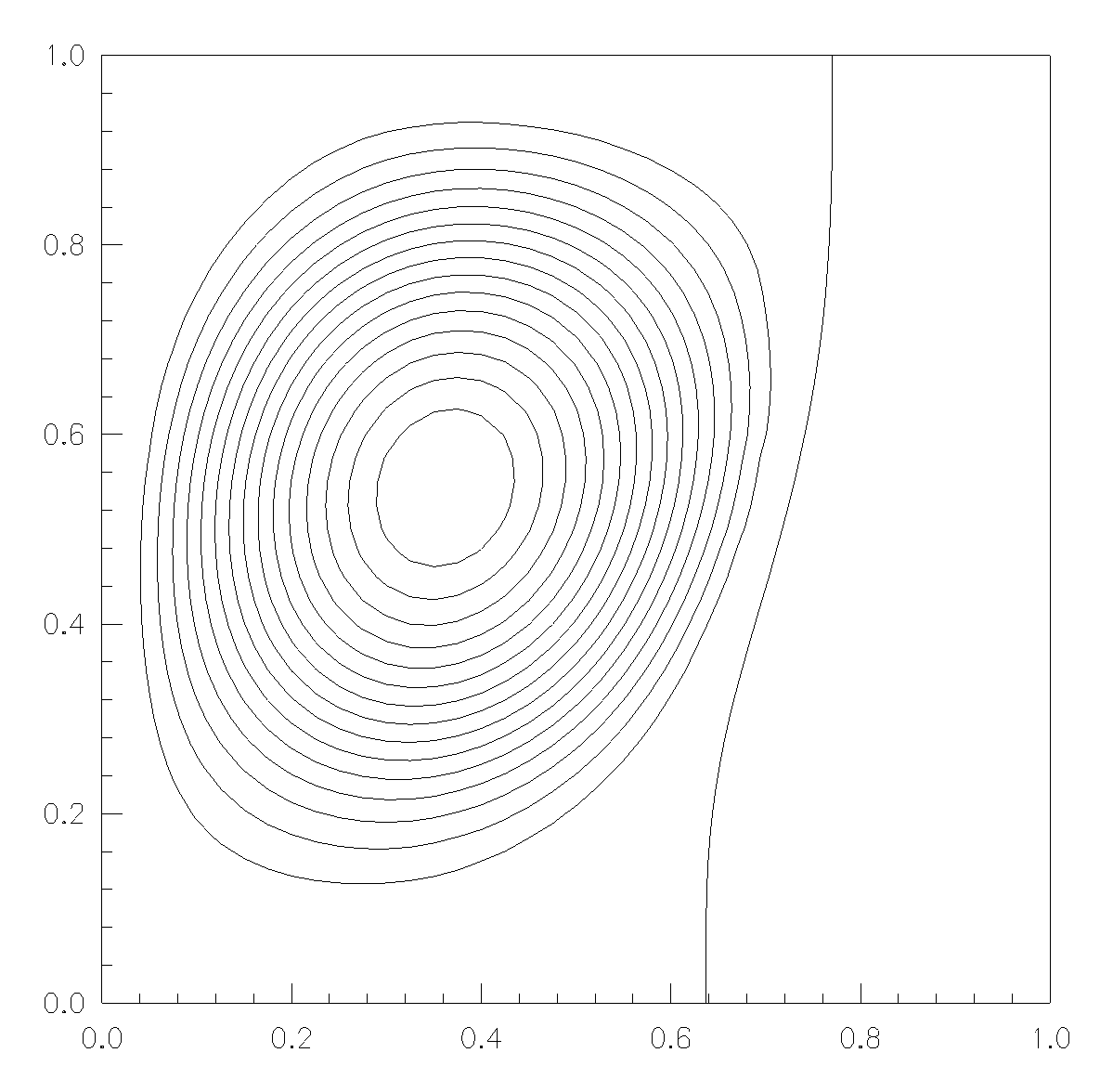
Figure 1. Solidification of gallium: steamlines and liquid-solid interface at steady-ststate at 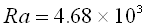
REFERENCES
- Chalmers: Principles of Solidification, John & Sons, inc., 1964.
- Rady, A. K. Mohanty: Natural Convection During Melting and Solidification of Pur Metals in a Cavity, Num. Heat Transfer, Part A, vo. 29, 1996, pp. 49-63.
- Brent, V.R. Voller, and K. J. Reid: Enthalpy-Porosity Technique for Modelling Convection Dffusion Phase Change: Application to the Melting of a Pure Metal, Num. Heat Transfer, vo. 13, 1988, pp. 297-318.
- R. Viswanath and Y. Jalura: Comparison of Different Solution Methodologies for Melting and Solidification Problems in Enclosures, Num. Heat Transfer, vo. 24, no. 1, 1993, pp. 25-41.
- Slattery: Momentum Energy and Mass Transfer in Continua, Krieger, New York 1978.
- V. Patankar: Numerical Heat Transfer and Fluid Flows, Springer-Verlag, New York, 1983.
- H. Van De Worst: A Fast and Smothly Converging Variant of Bi-CGStab for the Solution of Non-Symmetric linear Systems, SIAM, J. Sci. Stat. Comput., vo. 13, no.2, 1992, pp. 631-644.
NUMERICAL STUDY OF HEAT AND MASS TRANSFER DURING DIRECTIONAL SOLIDIFICATION
Victoria Timchenko*, M. El Ganaoui**, A. Lamazouade**, D. Morvan**
Eddie Leonardi*, Patrick Bontoux** and Graham de Vahl Davis*
*School of Mechanical and Manufacturing Engineering
University of New South Wales, Sydney, Australia 2052
* Département de Modélisation Numérique
Institut de Recherche sur les Phénomènes Hors Equilibre
Unité Mixte de Recherche CNRS 6594
1, rue Honnorat, 13003 Marseille, France
ABSTRACT
Melting and solidification problems are very important in manufacturing processes such as crystal growth of semiconducters, and casting and welding of metals and alloys. For semiconductors, the resulting structure of crystals is strongly affected by heat transfer and convection occurring in the melt. In pure materials the solid-liquid interface is sharp and corresponds to an isotherm. In these situations a front tracking method based on moving grids can be used. For alloys which solidify over a temperature-range, implementation of front tracking methods becomes difficult, particularly when a mushy zone exists. A fixed grid single domain approach (commonly called the enthalpy method) can be used succesfully for modelling various complicated phase-change systems including dendritic structures,.
A computational study of heat and mass transfer inside a vertical crystal growth ampoule during a remelting operation has been conducted. The governing equations for conservation of momentum, energy and species have been solved in the melt and in the crystal using a homogenisation technique. In this technique the solid-liquid mixture is represented as a single continuum medium defined after averaging operations performed for each species and each phase present in the system. The main advantage of this method is its ability to solve solidification problems of both pure and alloy materials without the necessity to follow the movements and deformation of the melt-crystal interface.
In this paper we present numerical simulations of crystal growth in a vertical Bridgman configuration. The effects of moving temperature boundary conditions on the accuracy of the predicted shape of the solid-liquid interface during solidification are investigated.
Numerical solutions are obtained based on a fixed grid single domain (enthalpy) method using two different approaches - finite volume with primitive variables and finite differences vorticity-stream function formulation.
Two cases are presented to model vertical Bridgman crystal growth: firstly one with a moving temperature profile imposed along the vertical wall of a motionless ampoule and secondly one with the ampoule translated with constant speed whilst the temperature boundary conditions are fixed in space. In theory these two approaches are identical; however in practice the implementation of moving temperature boundary conditions is susceptible to discretization errors.
In the latter case, the temperature profile is assumed to move at an average given speed V, corresponding to a Peclet number  , and the motion is performed in a discrete way by steps of , and the motion is performed in a discrete way by steps of  . The system is then computed with two discrete time scales: . The system is then computed with two discrete time scales:  for the movement of the boundary conditions and for the movement of the boundary conditions and 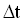 for the time intergration of the melt-solid phase equations. for the time intergration of the melt-solid phase equations.
Since the temperature is moved at discrete time steps it is found that the shape of the interface is strongly dependent on the time step chosen. This problem can be avoided by either subdividing the time step for which the equations are solved (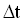 < < ), thus obtaining more accurate solutions or performing internal iterations at each time step ( ), thus obtaining more accurate solutions or performing internal iterations at each time step (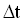 = = )to ensure correct coupling of all the equations and boundary conditions. )to ensure correct coupling of all the equations and boundary conditions.
Solidification in a vertical axisymmetric cylinder is presented in Figure 1, for  , , , Ra=1000. Solutions have been computed for , Ra=1000. Solutions have been computed for  and various and various  to to  (corresponding to 0 to 100 intermediate steps per (corresponding to 0 to 100 intermediate steps per ). It is clearly shown that progressive subdivisions of the time step significantly alters the interface shape and flow pattern. ). It is clearly shown that progressive subdivisions of the time step significantly alters the interface shape and flow pattern.


The flow patterns, solidus and liquidus are shown in Figure 2, for a two-dimensional rectangular ampoule of aspect ratio 5,  and Ra=1000. Calculations have been undertaken for three different time steps, and it was found that the solutions were time step independant, providing sufficient internal iterations were performed. and Ra=1000. Calculations have been undertaken for three different time steps, and it was found that the solutions were time step independant, providing sufficient internal iterations were performed.
Figure 3 shows the effect of internal iterations on the interface shape and position.
REFERENCES
- Bennon, W. and Incropera, F., A continuum model for momentum, heat and species transport in binary solid-liquid phase change systems: 1 model formulation, Int. J. Heat Mass Transfer, Vol. 30, No.10, pp 2161-2170, 1987.
- Voller, V.R., Brent, A.D. and Prakash, C., The modelling of heat, mass and solute transport in solidification systems, Int. J. Heat Mass Transfer, Vol. 32, pp 1719-1731, 1989.
HEAT TRANSFER AND GAP FORMATION IN CONJUGATE BODIES
S. L. Lee and C. R. Ou
Department of Power Mechanical Engineering
National Tsing-Hua University
Hsinchu 30043, TAIWAN
Tel/Fax: 886-3-572-8230
Heat transfer through conjugate bodies has many applications in industry and in natural. The mold-casting system is one of the examples. In the present study, an integration scheme is proposed for the interaction of heat transfer, thermal stress and thermal deformation in a couple of conjugate bodies. For convenience, a description on the derivation of the displacement equation and the integration scheme is presented briefly.
The relationship of stress and strain in two-dimensional elastic bodies is expressible as
 (1) (1)
 (2) (2)
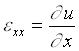 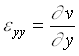  (3) (3)
where  denotes the displacement and denotes the displacement and  is a thermal strain due to a temperature change is a thermal strain due to a temperature change  . Substitution of equation (3) into equations (1) and (2) yields . Substitution of equation (3) into equations (1) and (2) yields
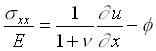  (4a) (4a)
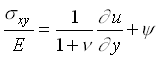  (4b) (4b)
where
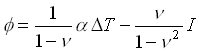  (5a) (5a)
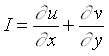  (5b) (5b)
This leads to the displacement equations
 (6) (6)
 (7) (7)
based on the equilibrium equation without body force.
Let W, P, E be three successive grid points at (xi-1, yj), (xi, yj), (xi+1, yj) and the subscript symbol 178 \f "Symbol" \s 12²}i,jsymbol 178 \f "Symbol" \s 12²} denote the value of a function at the point (xi, yj). Both the elastic modulus E and the Poisson ratio  are piecewise continuous functions in the domain of are piecewise continuous functions in the domain of  on y = yj. Next, let Eq.(6) be split up into a system of two ordinary differential equations on y = yj. Next, let Eq.(6) be split up into a system of two ordinary differential equations
 (8) (8)
 (9) (9)
where  is an unknown function of x and y. Integrating Eq.(8) with respect to x twice in the interval is an unknown function of x and y. Integrating Eq.(8) with respect to x twice in the interval  along the line y = yj, one obtains along the line y = yj, one obtains
 (10) (10)
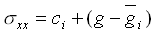 (11) (11)
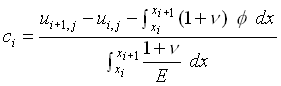 (12) (12)
where g(x) is an antidifferential of the function  with respect to x. The notation with respect to x. The notation  denotes the weighted average of the function g(x) over the interval denotes the weighted average of the function g(x) over the interval  with respect to (1+symbol 110 \f "Symbol" \s 12n)/E with respect to (1+symbol 110 \f "Symbol" \s 12n)/E
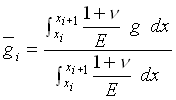 (13) (13)
Similarly, the displacement u and the stress symbol 115 \f "Symbol" \s 12sxx in the interval  along the line y = yj have the form along the line y = yj have the form
 (14) (14)
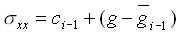 (15) (15)
Upon imposing the condition of continuous stress at x = xi on Eqs.(11) and (15), i.e.
 (16) (16)
one gets a relationship between the displacements at the three successive grid points (xi-1, yj), (xi, yj), (xi+1, yj) as
 (17) (17)
 , ,  (18) (18)
 (19) (19)
 (20) (20)
where  , ,  and the approximation and the approximation
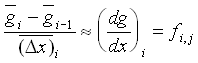 (21) (21)
has been employed.
Finally, discretize Eq.(9) with the same procedure and adds it to Eq.(18). This yields the integration scheme for the partial differential equation (6)
 (22) (22)
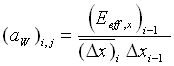 , , 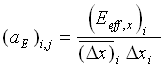 (23) (23)
 , , 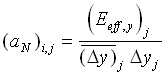 (24) (24)
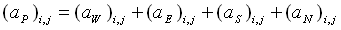 (25) (25)
 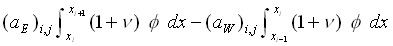  (26) (26)
where the unknown function  has been canceled. has been canceled.
It is interesting to note that (Eeff,x)i is the effective elastic modulus under the effect of the Poisson ratio symbol 110 \f "Symbol" \s 12n in the interval  on the line on the line  . In case there is a gap (E = 0) existing in the interval . In case there is a gap (E = 0) existing in the interval  , the effective modulus would be zero such that , the effective modulus would be zero such that  = 0. As a result, the displacement at the grid point (xi+1, yj) does not have a direct influence on that at (xi, yj). This is consistent with the physical reasoning. Thanks to the feature of integration, the integration scheme is equally applicable to heat conduction with thermal conductivity of piecewise continuous function. In the present study, the integration scheme is applied to a couple of conjugate bodies. Satisfactory results of gap formation and heat transfer between the two conjugate bodies are observed. = 0. As a result, the displacement at the grid point (xi+1, yj) does not have a direct influence on that at (xi, yj). This is consistent with the physical reasoning. Thanks to the feature of integration, the integration scheme is equally applicable to heat conduction with thermal conductivity of piecewise continuous function. In the present study, the integration scheme is applied to a couple of conjugate bodies. Satisfactory results of gap formation and heat transfer between the two conjugate bodies are observed.
PATTERNS OF TURBULENT HYDRODYNAMIC OCCURENCES IN SMALL VOLUME ROTOR MIXERS
Dr. Nikolai S. Shulaev
Sterlitamak Branch of Ufa State Petroleum Technical University, 453118, Sterlitamak, Russia
ABSTRACT. A theoretical investigations of the turbulent mixing of liquids in rotor pulsation
apparatus has been carried out. Discoveries were made in correlations of determination of
displacement deformation, pressure, dissipated power dependence upon construction
peculiarities of the apparatus and parameters of treated media. The coincidence of measured
and calculated values of power shows that the performed model gives an adequate description
of real processes.
THE DISPERSED BUBBLES TWO-PHASE FLOW MODEL : THEORY AND APPLICATION
Mohand KESSAL
Département Energétique . I N H . Boumerdes . 35000 . ALGERIA.
1. ANALYSIS
Mathematical models are generally fixed for the principal established two-phase flow patterns. If we
suppose a thermal and mechanical equilibrium between the phases , the conservation equations for each
fluid can be written:

where : k= g,l ( gas or liquid ) ; W= Ug - Ul
Ug and Ul are respectively the speeds of the gas and the liquid across a transversal area of the
pipe. The averaged pressures of the phases are supposed to be equal .
This system form a set of 4 equations for 4 unknown quantities P , a , Ug , and Ul .Generally the
resolution of this system by standard methods gives two real and two complex roots , which means that
it is not hyperbolic . In others words, the Cauchy problem for this system is ill-posed.
To face these difficulties it is proposed to replace gaseous momentum equation (2) by an other which
gives the dynamic interaction between bubbles and liquid. This equation is deduced from the one
obtained by considering the motion of a bubble in a liquid . It is also deduced from the one obtained by
considering the motion of a massless sphere in unbounded incompressible and inviscid fluid :

It is pratical to rewrite the relation (3) more realistically by adding the effects of gravity and the drag
forces . If we admit that this relation (which is valid for one bubble) can be applied for several
bubbles in the fluid (by neglecting the interactions between them), it can be written under a more
explicit form by introducing a mean velocity (Uo) of the mixture and the void fraction a.
The relation (3) associated to (1) and (2), instead of gas momentum equation, gives a hyperbolic
system which has 4 real and distinct roots :

Where W = Ug - Uo
Z and F are function of a, P, Ug, Ul and the physical properties of the phases and the pipe wall .
Integrating the obtained new system along the above characteristc directions gives the following 4
compatibility equations :

The coefficients Di ( where i=4 ) are function of a, P, Ul, W and of the physical
characteristics of the two fluids and the wall pipe.
2. RESULTS AND DISCUSSION
For bubbly flows obeying to equations (1), (2) and (3) we can predict critical flow from the criterion
that suppose that a stationary wave in the throat of the nozzle is possible. Experimental results with
bubbly flow through a Laval nozzle have been reported by some authors . They measure Ug, Ul, ao and
a (respectively the curves 1, 2, and 3 in Fig. 2.1) in the throat and their data provide us with an
opportunity to verify the validity of our model (curve 4 in Fig.2.1) which agrees relatively with our
formulation.

In the study of sound and shock waves in liquids containing bubbles, it is deduced that from the
analysis of spherical particles with low concentration, one can show that W = 0 for slow frequencies of
the sound velocity. In the case of high frequencies (W ¹ 0) the viscous forces will be negligable and
the bubbles move under the action of inertial forces which are proportional to the relative
acceleration (3). The previous compatibility equations allow to verify this behaviour.
When W = 0 the equation system (1) (2) (by introducing a mean density) allow for example to study of
the transients flows with gaseous cavitation. The second case is illustrated by Fig.2.2 for a fast closer
valve after a pump discharging in a pipe with a small diameter and length.

The obtained equation system (1), (2) and (3) ,with respect to the behaviour of the bubbles in the liquid
permits to study the particularities of the two-fluid model and the homogeneous model. In the first case
beside the critical flow, other flow patterns can be carried out with some improvements.
NOTATION
|
af |
wave velocity in a quiescent mixture |
Dh |
hydraulic diameter |
|
Uo |
mean velocity of the mixture |
q |
angle of inclination of pipeline |
|
S |
cross sectional area of the pipe |
P |
pressure |
|
x |
distance |
f |
friction loss coefficient |
|
t |
time |
a |
void fraction |
|
r k |
volumetric mass of the fluids |
t |
volume of the bubble |
|
ao |
experimental wave velocity in the throat |
|
|
THE RESONANCE OF NATURAL CONVECTION IN A CAVITY CONTAINING TIME PERIODIC INTERNAL SOURCES
A.Cihat BAYTAÞ
Istanbul Technical University,Institute For Nuclear Energy,
80626 MASLAK ,ISTANBUL,TURKEY
E-Mail: baytas@sariyer.cc.itu.edu.tr
INTRODUCTION
Natural convection of fluid media in cavities has received considerably attention over the past few decades, largely due to a wide variety of applications, which include reactor insulation, energy storage, cooling of radioactive waste containers, nuclear reactor safety analysis and design and post-accident heat removal in nuclear reactors, etc.
Many studies have been published on convection in enclosures. Kazmierczak et. al1. investigated the effect of the oscillating surface temperature on the fluid flow and heat transfer within the cavity. Lage and Bejan2 studied the resonance between enclosed natural convection and pulsating wall heating.
The present investigation is motivated by a problem encountered in the analysis of severe nuclear reactor accidents, heat is generated in the core debris harshly as a result of radioactive decay. The enlargement of decay heating of core debris by exoergic reactions especially with metallic constituents of core debris is a very important event of reactor accident. It is thought that any zirconium cladding around the fuel rods would be completely oxidised to ZrO2 during core degradation. The entrance of the ZrO2 promptly starts dramatic rises in the melt temperature. The heat generation keeps on oscillating due to intermittent energy released from the metallic reactions in the debris, and the melt temperature do not remain constant during the accident. However, in many of the applications mentioned above, the internal energy sources vary with time and, therefore, in reality, a transient or unsteady convective flow follows. Namely, the generated heat in the enclosure is of an unsteady or oscillatory nature.
The main focus of the present paper is to consider the unsteady laminar natural convection in a square enclosure containing uniformly distributed internal heat source (q/ / / ) which is changed sinusoidally with time (q/ / / = q0/ / / + A Sin(2p t/P)). The strength of internal energy source varies sinusoidally about a mean value with amplitude (A) and period (P). The cyclic variation of the strength of internal energy source approximates the oscillating heat generation in the reactor as mentioned before. The effect of oscillating internal heat source on the temperature and fluid fields, average Nusselt numbers on the walls, overall midplane Nusselt numbers maximum temperature variation in enclosure will be presented.
MATHEMATICAL FORMULATION AND SOLUTION PROCEDURE
The cross-section of the two-dimensional cavity is square and the all walls are considered isothermal (the rigid conducting walls).The basic equations of unsteady laminar free convection are the Navier-Stokes equations. Since the pressure field is not of primary interest in this investigation, it is eliminated by taking the curl of Navier-Stokes equations. The Navier-Stokes equations yield the vorticity transport equation. The non-dimensional form of the governing equations are obtained for incompressible flow and Boussinesq approximation. The method for the numerical computation was the two-dimensional finite-differences control-volume method. In this investigation, a staggered grid procedure was used in primitive variables with a power-law differencing scheme and a fully implicit scheme for evaluating the time derivatives . The governing equations are solved by using the Alternating Direction Implicit method. The stream function equation is solved by the Successive-Over-Relaxation procedure . Relaxation was used to aid the convergence in solving the vorticity equation, although it was not needed in the solution of the energy equation. Optimum overrelaxation parameter for solution of stream function equation is 1.78. Here, the value of convergence parameter (10-5) was found to be adequate, since a further reduction in it did not significantly effect the results and did increase the computational effort. A non-uniform grid (31x31) was used in all of the simulations. The density of grid is higher near the walls of the enclosure where sharp gradients of velocity and temperature are expected. The code was checked for accuracy against the earlier published experimental and numerical results for Ra=105 and Pr=7 . Excellent agreement has been obtained between the results to validate the computer code used in this study. The dependence of the results on the time step have been tested. A suitable dimensionless time step is 3x10-5 in this investigation.
RESULTS AND DISCUSSION
In this investigation, a total of five numerical simulations were accomplished for different amplitudes (0,0.5,0.5,0.2,0.2) for Sim 1,2,3,4,5,respectively, and periods (0.103,0.056,0.09,0.07). The Prandtl and Rayleigh numbers and aspect ratio of the cavity were all held fixed throughout this investigation in order to focus our attention on the parameters that directly pertain to the oscillatory internal heat source. The first study for dimensionless amplitude a=0 was performed to compare between presented results and previous experimental and numerical results, in addition to the understanding the difference between sinusoidally driven and not driven (a=0) internal source results. If the frequency of the periodic driving force is equal to any one of the natural frequencies of the body, resonance can occur. As seen in this study, the problem is periodic and it has two or more fundamental frequencies. Both of these selected fundamental periods are 0.103 (sim 2) and 0.056 (sim 3). For this reason, resonance can be seen for Sim.2 and Sim.3 because both of these simulations are driven sinusoidally with dimensionless period p=0.103 and 0.056, respectively. In these cases, the amplitudes of sinusoidally driven source are equal to the half of the mean heat source. Fast Fourier Transform is used to determine the resonance of sinusoidally driven internal source system.. Power Spectrum analysis of the time series helps us to find the frequencies of the system.
The main conclusion reached in this investigation is that if the frequency of the periodic driving force is equal to any one of the natural frequency of this problem, resonance can occur and the convection heat transfer is increased in enclosure. The values of average Nu number at walls and maximum temperature of enclosure are increased for Sim.2 and Sim.3. Because driving periods of Sim.2 and Sim.3 are equal to natural frequency of original problem (Sim.1) which was driven by a constant source. For Sim.2 and Sim.3, heat transfer are periodic like Sim.1 but the periodic oscillatory nature of the Sim.1 (a=0) are destroyed if the driving period was different from its natural frequencies. This can be shown in Sim.4 and Sim.5. It is evident that heat transfer mechanism is strongly dependent on the periods of external reactions in any cavity which has a uniform internal heat source.
Furthermore, if the cavity contains any periodically varying heat source or periodically varying reactions inside, because of resonance it is necessary to know about its fundamental frequencies and also the frequencies of the periodically driving heat source.
REFERENCES
- Kazmierczak,M., Chinoda,Z., Buoyancy Driven Flow In An Enclosure With Time Periodic Boundary Conditions, Int.J.Heat Mass Transfer, Vol.35 No.6, pp 1507-1518, 1992.
- Lage,J.L., Bejan,A., The Resonance of Natural Convection In An Enclosure Heated Periodically From The Side, Int.J.Heat Mass Transfer ,Vol.36 No.8,pp 2027-2038,1993.
ON PHASE TRANSFORMATION FRONT PROPAGATION IN ELASTIC BODIES
Victor A.Eremeyev and Dmitry M.Sotnichenko
Mechanics and Mathematics Department
Rostov State University, Rostov-on-Don, Russia
In this article the connected problem of solidification or melting front propagation in elastic body is considered. The conditions on the moving inter-phase surface have been obtained with assumptions of thermoquasistatics and on the basis of the general conservation laws for mass, impulse, energy and with regard to the second thermodynamics law in the form of the Clausius-Duhem inequality1. The equations in a firm elastic phase have been formulated in general kind taking into account the finiteness of deformations. The inter-phase surface energy influence has been taken into account. Influence of impurity has been also considered. As well as any problem with unknown boundary, the boundary-value problem we obtained is non-linear even if equations in each phase are linear.
As an examples, two problems have been considered: the elastic cylinder solidification and flat phase boundary movement in a half-space. The last problem has been considered with the assumption of smallness of the elastic phase deformations.
The problem of phase transformations description in solids is one of the urgent and important problems of physics and solid mechanics. Its importance is stipulated by the fact that the majority of materials, used in modern engineering, undergo phase transformations in the process of their manufacturing or their exploitation or when they contact the media with phase transformations. Examples of processes, in which it is necessary to take into account mutual influence of deformation and phase transformations, are the growth of crystals, freezing of ground, formation of an ice cover, solidification of metal in a melting form, solidification of products made of polymeric materials, solid-phase transformations in steel, in alloys and in minerals, phase transformation in the planets core, manufacturing of piezo-materials. The wide spectrum of phase transformations is observed in liquid crystals.
Within the framework of the non-linear mechanics of solid medium phase transformations have been considered in a large number of papers (for example, see2-6). Some first results on plane phase boundary propagation obtained in6 . The stability problem for the deformed bodies, which undergo phase transformation is of special interest. Besides, fewer papers are devoted to this topic. We want to note, that the necessity of using the non-linear equations for phase transformation modeling is stipulated by the general reason – each of phases can be described by the non-linear conditions, especially in a vicinity of inter-phase boundary. Besides, some parameters, describing phase transformation can be rather great, such as: difference of phase density, symmetry group. This can lead to arising a large field of stress and strain. Moreover, the presence of unknown phase separation surface, where boundary conditions are set up, makes a considered problem non-linear even if the equations in phases are linear. The non-linearity of a stressed-deformed solid problem also lead to the uniqueness problem and stability problem of the solution obtained.
We have considered both direct problem about determination of the fields of displacements and of temperature and of impurity concentration in the case of given initial conditions, and inverse problem of temperature change determination on the external body surface (boundary conditions), providing the given law of the phase boundary movement. The last problem is connected to the optimization and management of solidification process in metallurgy.
The analysis of influence of stress, arising during solidification, of non-linearity of conditions, of distribution of impurity, of surface energy and of other physical-mechanical factors on a movement of phase boundary has been given. Differences of the constructed solutions from the ones obtained on the basis of a classical Stefan problem have been also discussed.
For investigation of found solutions stability linearized equilibrium equations, heat transfer equations and boundary conditions on inter-phase boundary have been obtained. The last include along with small disturbance of temperature, displacements and concentration of an impurity, also a small vector of disturbance of a phase surface. Obtained homogeneous linearized initial-boundary problem describes indefinitely small deviations from some basic solution.
Unlike the available solutions of the stability problem of moving phase boundary within the framework of the Stefan problem (the so-called morphological stability problem), the taking into account the stress, that arises in a firm phase during solidification or fusion, can render considerable influence to process of the stability loss. For example, the instability caused by compressing stress can lead to buckling of the cover on the surface of the solidificated melt.
The application of the method of the boundary integral equations and the method of the boundary integral elements in the case of the linear equations in phase volumes has been proposed.
Acknowledgments
This work has been partially supported through a grant of the Russian Foundation of Basic Researches (No 96-01-01283).
REFERENCES
- Truesdell, C., A First Course in Rational Continuum Mechanics, The Johns Hopkins University, Baltimore, Maryland, 1972.
- James, R.D., The Propagation of Phase Boundaries in Elastic Bars, Arch. Rat. Mech. Anal. Vol. 73, No. 2, pp 125-158, 1980.
- Gurtin, M. E., Two-Phase Deformation of Elastic Solids, Arch. Rat. Mech. Anal. Vol. 84, No. 1, pp 1-29, 1983.
- Grinfeld, M.A., Continuum Mechanics Methods in the Theory of Phase Transformation, "Nauka", Moscow, Russia, 1990.
- Eremeyev, V. A. and Zubov L.M, On the Stability of Equilibrium of Nonlinear Elastic Bodies with Phase Transformations, Proc. USSR Academy of Science. Mech. solids. No. 2, pp 56-65, 1991.
- Eremeyev, V.A. and Sotnichenko D.M., On Propagation Phase Transformation Front in Elastic Bodies, Proceedings of 2nd Int. Conference "Modern Problems of Continuum Mechanics", Rostov-on-Don, September 19-20, 1996, vol. 1, pp 45-49.
NUMERICAL STUDY OF THE ONSET OF NATURAL CONVECTION BASED ON LYAPUNOV–SCHMIDT METHOD
Konstantin A. Nadolin
Mechanical and Mathematical Department,
Rostov State University, 344090 Rostov-on-Don, Russia
The Rayleigh–Benard problem is examined numerically by the non–Boussinesq approximation. We correctly derive this approximation from general equations for fluid whose specific volume depends linearly only on temperature and does not depend on pressure. Unlike the Oberbeck–Boussinesq approximation the negligibility of thermal expansion is not assumed in this model and all terms with coefficient of thermal expansion are taken into account. We assume the dynamic viscosity, the thermal conductivity and the specific heat of the fluid to be constant. We further assume that the work of pressure forces and viscous energy dissipation are negligible. We assume the boundaries of the layer are isothermal.
GOVERNING EQUATIONS
Let us consider an infinite horizontal layer of fluid between surfaces  and and  that is each kept at constant temperature – the lower at that is each kept at constant temperature – the lower at  , the upper at , the upper at  , with , with  . Each of these surfaces may be rigid or free but plane. Let us assume that the specific volume of the fluid linearly depends on temperature and does not depend on pressure. The dynamic viscosity coefficients, the thermal conductivity and the specific heat of the fluid are assumed to be constant, and the work of pressure forces and viscous energy dissipation are negligible. We introduce a coordinate system . Each of these surfaces may be rigid or free but plane. Let us assume that the specific volume of the fluid linearly depends on temperature and does not depend on pressure. The dynamic viscosity coefficients, the thermal conductivity and the specific heat of the fluid are assumed to be constant, and the work of pressure forces and viscous energy dissipation are negligible. We introduce a coordinate system  with the with the  axis directed vertically upwards and the axis directed vertically upwards and the  and and  axes lying in the plane of the lower boundary of the layer. The layer thickness axes lying in the plane of the lower boundary of the layer. The layer thickness  the temperature difference the temperature difference  and the convective ascent velocity and the convective ascent velocity  where where  is the free-fall acceleration and is the free-fall acceleration and  is the thermal expansion coefficient are taken as the scales of length, temperature, and velocity. The temperature is reckoned from the temperature at the lower boundary is the thermal expansion coefficient are taken as the scales of length, temperature, and velocity. The temperature is reckoned from the temperature at the lower boundary  . Under these assumptions the free convection equations in dimensionless variables have the form . Under these assumptions the free convection equations in dimensionless variables have the form
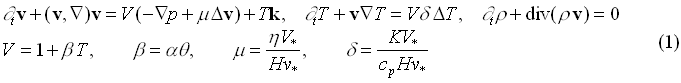
where  is the velocity vector, is the velocity vector,  is the temperature, is the temperature, 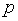 is the pressure deviation from the hydrostatic one with allowance for viscosity forces; is the pressure deviation from the hydrostatic one with allowance for viscosity forces;  and and  are the specific volume and the fluid density respectively; are the specific volume and the fluid density respectively;  is the thermal expansion parameter; is the thermal expansion parameter;  is the kinematic viscosity parameter, is the kinematic viscosity parameter,  is the Fourier number, are the dynamic viscosity and thermal conductivity coefficients and the specific heat of the fluid; is the Fourier number, are the dynamic viscosity and thermal conductivity coefficients and the specific heat of the fluid;  is the specific volume of the fluid at the temperature is the specific volume of the fluid at the temperature  , ,  is the is the  axis unit vector. The boundary conditions for the temperature have the form: axis unit vector. The boundary conditions for the temperature have the form:

The condition for the velocity at the rigid boundary is

and at the free boundary is

The idea of the reliable model assumptions and approaches to the derivation of these equations was recommended by V.I.Yudovich. To reflect the basic assumptions of the model we shall call our fluid as isothermally incompressible one and the equations (1) as the approximation of an isothermally incompressible fluid . .
It is interesting to compare the proposed model (1) with convenient Oberbeck–Boussinesq approximation. The main distinguishes between these two models of convective motion connect with the presence of the additional parameter  . When . When  is equal to zero the model (1) is the same as the Oberbeck–Boussinesq approximation. Therefore it may consider the model (1) as generalization of the Oberbeck–Bussinesq approximation that rigorously takes into account the effects of the temperature dependence of the specific volume (or mass density) of the fluid. This explicit relation between two models allows the quantitative estimation of the validity of the Oberbeck–Boussinesq approximation for concrete problem. is equal to zero the model (1) is the same as the Oberbeck–Boussinesq approximation. Therefore it may consider the model (1) as generalization of the Oberbeck–Bussinesq approximation that rigorously takes into account the effects of the temperature dependence of the specific volume (or mass density) of the fluid. This explicit relation between two models allows the quantitative estimation of the validity of the Oberbeck–Boussinesq approximation for concrete problem.
We examine the influence of the thermal expansion parameter  to the instability of the equilibrium of layer and to the onset of convective rolls. The boundary-value problems (1)–(4) have a steady-state solution corresponding to mechanical equilibrium with a linear temperature profile: to the instability of the equilibrium of layer and to the onset of convective rolls. The boundary-value problems (1)–(4) have a steady-state solution corresponding to mechanical equilibrium with a linear temperature profile:
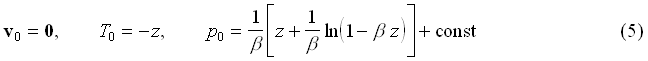
New solutions of (1)–(4) periodic in  and and  with periods with periods  , respectively with zero average pressure gradient along any of the horizontal directions are sought in the form: , respectively with zero average pressure gradient along any of the horizontal directions are sought in the form:
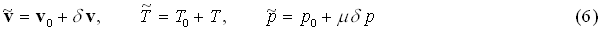
where  are unknown perturbations The government equations for perturbations are are unknown perturbations The government equations for perturbations are
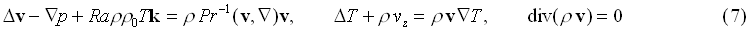
Here  and and  are the specific volume and the fluid density in equilibrium (5). We have introduced the Rayleigh number are the specific volume and the fluid density in equilibrium (5). We have introduced the Rayleigh number  and the Prandtl number and the Prandtl number  . The linearized equations (7) have the form: . The linearized equations (7) have the form:
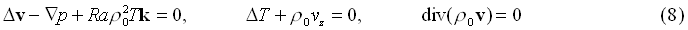
NUMERICAL RESULTS AND CONCLUSIONS
The important feature of the hydrodynamic stability problems and the convection problems especially is the presence of the hidden small parameter — the near-criticality or the amplitude of the perturbations. In this case the direct numerical simulation by relaxation requires much of computer time and special methods that use the small parameter technique are more suitable.
We applied the linearization method for linear stability analysis and the Lyapunov–Schmidt approach for weakly-nonlinear analysis . The numerical technique based on the solution of a series of homogeneous and non-homogeneous linear problems. The computing algorithms based on the numerical solution of the boundary-value problems by shooting technique and parameter movement. The object-oriented methodology and C++ language we have used for design and programming. . The numerical technique based on the solution of a series of homogeneous and non-homogeneous linear problems. The computing algorithms based on the numerical solution of the boundary-value problems by shooting technique and parameter movement. The object-oriented methodology and C++ language we have used for design and programming.
The horizontally periodic solutions (6) we search in the form:
 (9) (9)
Substituting (9) in (8) and separating the variables, we obtain spectral problem for a system of ordinary differential equations
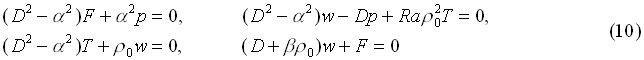

where 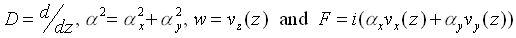 . The values of the minimized critical Rayleigh number . The values of the minimized critical Rayleigh number  and corresponding to it wave number and corresponding to it wave number  for (10)–(13) where for (10)–(13) where
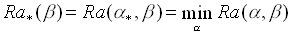
are given in the Table.. It has been established that the correction term for the critical Rayleigh number has the first order of  for all boundary conditions we examined. for all boundary conditions we examined.
Table.
The critical Rayleigh and wave number.
|
|
Rigid–rigid boundaries |
Free–free boundaries |
Rigid–free boundaries |
|
|
|
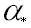
|
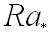
|
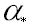
|
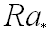
|
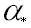
|
|
0.0 |
1707.7 |
3.12 |
657.5 |
2.22 |
1100.6 |
2.68 |
|
0.1 |
1461.4 |
3.12 |
562.6 |
2.22 |
932.7 |
2.68 |
|
0.2 |
1234.5 |
3.12 |
475.1 |
2.22 |
779.4 |
2.68 |
|
0.3 |
1025.3 |
3.12 |
394.7 |
2.22 |
640.1 |
2.69 |
|
0.4 |
837.3 |
3.12 |
321.6 |
2.22 |
514.4 |
2.70 |
|
0.5 |
666.0 |
3.12 |
255.2 |
2.22 |
402.3 |
2.71 |
|
0.6 |
512.2 |
3.13 |
195.8 |
2.23 |
302.8 |
2.72 |
|
0.7 |
376.1 |
3.15 |
142.9 |
2.24 |
215.9 |
2.74 |
|
0.8 |
256.5 |
3.16 |
96.5 |
2.26 |
141.5 |
2.76 |
|
0.9 |
151.9 |
3.17 |
55.8 |
2.28 |
78.1 |
2.83 |
For the weakly-nonlinear analysis by Lyapunov–Schmidt scheme we adopt the described earlier algorithm . As one the numerical results we pointed out the subcritical bifurcation that does occur in proposed model contrary to the Oberbeck–Boussinesq approximation. . As one the numerical results we pointed out the subcritical bifurcation that does occur in proposed model contrary to the Oberbeck–Boussinesq approximation.
REFERENCES
- Nadolin, K.A., Boussinesq Approximation in the Rayleigh–Benard Problem, Fluid Dynamics, Vol. 30, No. 5, pp.645–651, 1995. (Translated from Izvestiya Rossiiskoi Akademii Nauk, Mekhanika Zhidkosti i Gaza, No. 5, pp.3–10, 1995).
- Pukhnachov, V.V. Model of convective motion under low gravity, Proceedings of the VIIIth Europ. Symp. on Materials and Fluid Science in Microgravity, Brussels, Belgium, 1992, ESA SP–333, pp.157–160, 1992.
- Yudovich, V.I. Free convection and branching, Prikladnaya Matematika i Mekhanika, Vol. 31, No. 1, pp.101–111, 1967. (in Russian).
- Nadolin, K.A. AMPL — the computer program for the numerical analysis of stationary secondary solution by the Lyapunov–Schmidt method, Deposited at the All–Union Institute of Scientific and Technical Information, No.1177-B89, 1989. (in Russian).
NUMERICAL ANALYSIS OF UNSTEADY LAMINAR FORCED CONVECTION IN A RECTANGULAR CHANNEL
Ü. Uysal, N. Sözbir, Ý. Ekmekçi, H. Ý. Saraç*, Ý. Çallý
Department of Mechanical Engineering., Sakarya University, Sakarya, Turkiye
* Department of Mechanical Engineering., Kocaeli University, Kocaeli, Turkiye
ABSTRACT-This paper focuses on a numerical investigation of transient laminar forced convection in a rectangular duct due to a sinusoidal heat input at the inlet with hydrodynamically developed and thermally developing air flow. A numerical study of unsteady laminar forced convection in a rectangular duct, resulting from a periodic variation of the inlet temperature is presented. Numerical solution for the laminar thermal enterance problem with fully developed parabolic velocity profile is obtained under the boundary conditionof the fifth kind which is verified by the experiments. The experiments were conducted over with range of Reynolds number range is 1120b <0.24 Hz of the periodic heat input.The transient heat transfer problem is solved in the thermal enterance region of the duct. Numerical results are reported. A second order accurate explicit finite difference scheme is used in teh numerical solution to the energy equation. Numerical results are obtained with the fully developed parabolic velocity profile under the boundary condition of the fifth kind which was verified by the experiments.
|

