Using initial condition in Bayes rule, we can lead the Algorithm :

in this Algorithm, depend on observation data. In this study, parameter is fix value so Q is set to 0. Therefore the value of decided is only R, so the parameter depend on R.

NUMERICAL EXAMPLE

In this study, the computational grid (473 nodes, 840 elements) of finite element mesh is shown in Figure 1 , the incident wave of amplitude is estimated. The flow condition is a sine wave coming from the left side. The sine wave is as follows ;

In this case, each results which are given at observation points, are added to noise, and these data make use of observation data (Figure 2). According to the observation data, the amplitude is estimated. In this case, R is 0.0075, lumping parameter is 0.90 . The initial condition, in all nodes velocity and water elevation, set to zero.

In the observation points No.l No.2 No.3(Figure 1), the results of estimate amplitude are shown in Figure 3. In this case, the good agreement value are found by using various R. Next, observation point is only set to No.2, and the incident wave of amplitude changes into 1.5m and 2.0m. In this case, R is used same value which is used to lead the best agreement in case incident wave of amplitude is l.Om.

In this case, we estimate amplitude, which is fixed value. And, sensitive matrix is

CONCLUSION

We find that agreement value on incident condition is given by changing R, by this method. From Figure 3, each observation points are given by each R. Therefore, it is said that in case of observation points, R is set to each case. And father and father from incident points is bigger and bigger the slope of graph at l.Om of Y scale. In case same observation point, if changed dimension of size, R is same value.

This paper made use of shallow water equations as a basic equation, and parameter estimated incident wave of amplitude as a parameter estimation. The feature of this method is pointed out in the fact that Finite Element Method is incorporated into Extended Kalman Filter. It was estimated by this model case that the propriety of this method is right and reasonable.

REFERENCES

1. M.Kawahara, Finite Element Method, Gihoudo publishing, 1983.
2. T.Katayama, Applied Kalman Filter, Asakura publishing,1983.

Predictive Control Applied to Flood Control Problem

Kiyofumi SAKUMA and Mutsuto KAWAHARA
Dept. of Civil Engineering Chuo University
1-13-27 Kasuga Bunkyou-ku, Tokyo,Japan

1. INTRODUCTION

It is very important to control flood flow especially like Japan where it often happens, so various approaches have tried to the problem. Then this study presents a flood control problem operating dam gate to find optimal discharge objectively. As the method, predictive control theory is applied, which is the method that is able to determine the optimal one at any time, if possible to know some future data. And the purpose of this study is set to find optimal value which lower water elevation.

Its characteristics is on-line control which can determine the discharge getting predicted state values, and possible to recover ones on computing, if they have errors.

The behavior of water surface is governed by linear shallow water equation. It is discretized by finite element method and the phenomonon is analyzed.

2. BASIC EQUATION, BOUNDARY CONDITION

The wave propagation of reservoir is governed by two dimensional shallow water equation and represented as follows; equation as follows ;

where q is unit flux, h is water elevation, g is gravitational acceleration and h is water depth. Boundary conditions are given as follows ;

where S₁ and S₂ are entrance and exit boundaries , and S₃ is treated as land boundary condition.

3. FINITE ELEMENT METHOD

The analyzed domain is divided into triangle finite elements and weighted residual equations are given to them. And they are interpolated by Galerkin Method, finite element equation can be obtained as follows ;

where {X} is state vector, [M], [H] are coefficient matrices which are represented as follows ;

where F is interpolation function. Two-steps explicit method is applied to finite element equation (6), and represented as follows ;

where is lumped coefficient matrix, using lumping parameter e , mixed coefficient matrix is written as follows ;

4. PREDICTIVE CONTROL METHOD

4.1. State Equation

To argue control theory, Eqn.(6) is changed into state equation like (12) ;

where [A] [B] [C] are coefficient matrices,and [x],[u],[f] is state, control , force vectors respectively.

4.2. Performance Function

where [R] [Q] are diagonal terms of weighting matrices.

4.3. Stationary Condition

Control vector {u}_n which minimizes performance function J_n is represented as follows ;

4.4. State Prediction

Future state equation is represented as Eqn.(15) by descetizing Eqn.(12) with explicit Euler method.

If Eqn.(15) is substitued for each state vector obtained by Eqn.(14) , control vector {u} is represented as follows ;

where each matrice is represented as follows ;

5. NUMERICAL EXAMPLE

Numerical test is experienced at rectanglar mesh and Fig.l is the finite element mesh. Total number of nodes and elements are 33 and 40 respectively. Time increment D is 0.6 (sec), predicted state value is 60.0 (sec.). Fig.2 shows the time history of unit inflow flux at A point, and Fig.3 is the one of unit discharge flux at C point, where solid-line is control discharge and broken-line is non-control one. Fig.4-Fig.6 show water elevation at each point, and solid-line is controlled, broken-line is non-controlled ones.

6. RESULT

7. CONCLUSION

If it is possible to know certain state value constantly, water elevation is enough lowered compared with non-controlled case.

In short,it is said that predictive control theory is applicable for the problem which represents natural phenomena as basic equations so that it is useful for Hear Transfer Problem as real time control.

200 W. Packer Ave. Packard Lab. No: 19, Bethlehem, PA 18015-3085 USA 

The use of computational fluid dynamics (CFD) codes in understanding the flow behavior in complex transitional and/or turbulent thermo-fluids systems has been extensively increased in recent years. Research on low-dimensional modeling (LDM) of nonlinear dynamical systems has been also gaining considerable attention. Certain fluid systems exhibit chaotic behavior through the nonlinear interaction of small number of degrees of freedom, enabling us to represent transition process in phase space by low-dimensional dynamical behavior. This remarkable outcome furnishes the basis for the development of LDMs of transitional thermo-fluid systems. These developed models replace the system of governing partial differential equations (PDEs) with a relatively small set of ordinary differential equations (ODEs) that captures the underlying dynamical behavior of the thermo-fluids system. Direct numerical simulations (DNSs) of transitional and turbulent convective flows in complex geometries, such as grooved and vertical channels, require tremendous computational time and power. Thus, accurate and valid low-order approximations to the full model may enable us to employ the techniques of dynamical system theory in investigating bifurcation, stability and control characteristics of complex transitional thermo-fluid systems.

Methods, such as Fourier-Galerkin, Chebyshev-Galerkin, trigonometric functions and orthogonal polynomials are widely used to transform a system of PDEs into a set of ODEs. However, these methods use general basis functions in the expansion leading to large system of ODEs. It is important that LDMs are constructed by expanding the unknown functions in terms of basis functions that are constructed for each system separately and reflects the dynamical behavior of the system in the vicinity of some flow controlling parameters. Proper orthogonal decomposition (POD, the method of empirical eigenfunctions, Karhunen-Loeve expansion) first introduced in the fluid mechanics community by Lumley [1], is a candidate for obtaining a set of optimal basis functions. Berkooz et al. [2] give a rigorous review of POD in the analysis of turbulent flows. The method of snapshots has been introduced by Sirovich [3] as an efficient way of extracting the empirical eigenfunctions of large data sets. Using snapshots POD, Deane et al. [4] and Sahan et al. [5-6] constructed low-dimensional dynamical models for transitional isothermal and nonisothermal flow in a periodically grooved channel. Gunes et al. [7-8] analyzed buoyancy-driven convective flow system in a vertical channel with discrete heaters. Liakopoulos et al. [9] studied free convective flow in a differentially heated cavity.

This paper focuses on DNS and low-order dynamical representation of transitional flow and heat transfer in a periodically grooved channel relevant to forced convective air (Prandtl number, Pr=0.71) cooling of electronic systems. The governing PDEs (conservation of mass, momentum and energy) of the thermo-fluid system are solved by a spectral element method. Spontaneously oscillatory solutions are calculated for a supercritical value of Reynolds number, Re=750. POD is used to extract empirical eigenfunctions, identify and define the spatio-temporal (coherent) structures of the thermo-fluid system. POD enables us to represent the velocity and temperature fields in an optimal way. The 6 largest normalized eigenvalues of the most energetic eigenmodes and their respective contribution to the flow and temperature fluctuation energy are given in Table 1.  

Table 1

Eigenvalues of the 6 Most Energetic Velocity and Temperature Modes and Their
Respective Contributions to the Total Flow and Temperature Fluctutation Energy

As observed in Table 1, eigenvalues come in pairs of comparable magnitude and the major portion of the fluctuation energy is captured by the first two modes of velocity and temperature. The first four modes for both velocity and temperature fields contain almost all flow and temperature fluctuation energy. It is found that first two most energetic eigenfunctions for each field variable contain the large scale features of the thermo-fluid system while higher modes, with lesser energy level, capture the small scale features. These organized spatio-temporal structures occur in pairs with a phase-shift of approximately a quarter-wavelength in the streamwise direction. The same observations are true for all velocity and temperature eigenfunctions. Eigenfunctions and coherent structures of the thermo-fluid system are identified as standing and travelling waves respectively.

A low-dimensional dynamical system of nonlinear ordinary differential equations is obtained by using the empirical eigenfunctions as basis functions in a truncated series expansion and applying Galerkin projection (GP). The system of nonlinear ODEs is the representative form of the LDMs of the thermo-fluid system under investigation. The number of modes retained in the series expansions for both modes determines the size of the reduced models. It is found that expansion coefficients computed based on low-dimensional dynamical model's predictions and by direct projection of the full model simulation data are found to be in very good agreement. Four modes for each field variable is the smallest set capable of predicting stable, self-sustained oscillations with correct amplitude and frequency. Retaining fewer modes in the truncated series expansion either does not produce stable self-sustained oscillations in time or fails to predict the correct amplitude of the oscillations. Keeping more modes than necessary in the expansion may reduce the accuracy and restrict the validity of the LDMs due to the noise introduced by the low-energy level higher modes. At Reynolds numbers close to the "design" conditions, LDMs successfully estimate the dynamical attributes of the thermo-fluid system. At higher Reynolds numbers, the reduced models predict quasi-periodic route to chaos.

The developed low-dimensional models may be used in the description of dynamical behavior of spatio-temporal structures, in the bifurcation and stability analysis of transitional thermo-fluids systems in complex configurations, in the study of "off-design" system dynamics and in exploring the active and passive intelligent flow control ideas with the use of artificial neural networks (ANNs). 

Key Words: transitional flow; forced convection in grooved channels; proper orthogonal decomposition; Karhunen-Loeve expansion; empirical eigenfunctions; spatio-temporal (coherent) structures; low-dimensional (order) models; quasi-periodic route to chaos. 

1. J.L. Lumley, 'The structure of inhomogeneous turbulent flow', In Atmospheric Turbulence and Radio Wave Propagation, (ed. A.M. Yaglom and V.I. Tatarski), Nauko, Moscow, 160-178 (1967).
2. G. Berkooz, P. Holmes and J.L. Lumley, 'The proper orthogonal decomposition in the analysis of turbulent flows', Annual Review of Fluid Mechanics, 25, 539-575 (1993).
3. L. Sirovich, 'Turbulence and dynamics of coherent structures: I-III.', Quarterly of Applied Mathematics, 45, 561-590 (1987).
4. A.E. Deane, I.G. Kevrekidis, G.E. Karniadakis, S.A. Orszag, 'Low-dimensional models for complex geometry flows: application to grooved channels and circular cylinders', Physics of Fluids A, 3(10), 2337-2354 (1991).
5. R.A. Sahan, H. Gunes and A. Liakopoulos, 'Low-dimensional models for coupled momentum and energy transport problems', In Cooling and Thermal Design of Electronic Systems, (ed. C. Amon), ASME HTD-319/EEP-15 , 1-15 (1995).
6. R.A. Sahan, A. Liakopoulos and H. Gunes, 'Reduced dynamical models of nonisothermal transitional grooved- channel flow', Physics of Fluids A, 9(3), 551-565 (1997).
7. H. Gunes, R.A. Sahan and A. Liakopoulos, 'Low-dimensional representation of buoyancy driven flow in a vertical channel with discrete heaters', In Enhancing Natural Convection Cooling of Electronic Systems and Components, (eds. A. Ortega and S.P. Mulay), ASME HTD-303, 125-137 (1995).
8. H. Gunes, A. Liakopoulos and R. A. Sahan, 'Low-dimensional description of oscillatory thermal convection: the small Prandtl number limit', Theoretical and Computational Fluid Dynamics, in-press, (1997).
9. Liakopoulos, P.A. Blythe and H. Gunes, 'A reduced dynamical model of convective flows in tall laterally heated cavities', Proceedings of the Royal Society of London A, 453, 663-672 (1997).

INTEGRAL TRANSFORM SOLUTION OF THE TURBULENT BOUNDARY LAYER EQUATIONS IN STREAMFUNCTION-ONLY FORMULATION

L.C.G. Pimentel ^(*), RM. Cotta ^(*), and S. Kakaç
Department of Mechanical Engineering
University of Miami
P.O. Boz 248294 - Coral Gables
Florida - 33124-0624 - USA
^(*)Permanent address: - Laboratory of Transmission & Technology of Heat
Mechanical Engineering Dept. - Universidade Federal do Rio de Janeiro
EE/COPPE/UFRJ
Cidade Universitária - C.P. 68503 - Rio de Janeiro, RJ - 21945-970 - BRASIL

ABSTRACT. Developing turbulent flow between parallel plates is analyzed, by making use of the generalized integral transform technique to obtain a hybrid numerical-analytical solution of the governing boundary layer equations for incompressible steady flow. The streamfunction-only formulation is preferred over the primitive variables one, in light of the improved convergence rates achievable, for the related eigenfunction expansions, with the former choice. Also, a well-established algebraic turbulence model is adopted for the required flow diffusivities, and numerical examples are employed to illustrate the computational performance of the proposed approach.

In recent years, many advances have been made in the study of the advective modeling methods with higher accuracy and computational efficiency for the advection equation. These methods are sometimes named as 'shock-capturing' schemes, or as 'TVD(total-variation diminution)' which are referring to the oscillation-suppression . To achieve a satisfactory numerical modeling of convection is always a dilemma to the researchers in the field of computational fluid dynamics. On the one hand, the second-order methods or other higher-order methods give high-order accuracy, but at the same time, nonphysical oscillatory behavior in regions where steep gradients exist may be generated. Central difference scheme(CDS) is one of the example. This scheme may lead to unrealistic oscillatory behavior in an implicit solution or to non-convergent solutions in an explicit computation in regions where convection strongly dominates . On the other hand, using the classical first-order upwind difference scheme(UDS), the oscillations will be replaced by the unacceptable global artificial diffusion. In 1979, proposed the quadratic upstream interpolation for convective kinematics scheme (QUICK) for quasi-steady flow situations. The methods have the desirable simultaneous properties of high accuracy, inherent numerical convective stability, algorithmic simplicity and a physically appealing foundation. Bram Van proposed the MUSCL approach, which stands for monotone upstream-centered schemes for conservation laws. In this method, in order to generate higher spatial approximations, the state variables at the interfaces are obtained from an extrapolation between the neighboring cell averages.

In this paper, a new technique, Characteristic Convective with Monotonic Conservation (CCMC) Scheme, is proposed. The procedures of the method in solving the pure one dimensional convective equation are presented. Finally, a set of bench-mark test problems, which includes three critical test profiles and has been tested in Leonard's , is used to exam the new scheme. 

 Consider the unsteady one-dimensional pure convection equation of a scalar, ,

(1)

Where u is velocity. We consider a 1-D domain divided uniformly in the x-dir at points for with . Eqn. (1) can be integrated in time over a time step and in space over a control volume at station from to . This gives

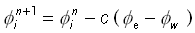
where is the Courant number. The subscript notation refers to the west and east side of the control volume faces. The superscript designates the time level. How to determine a better convective interpolation of the control volume faces is a key in solving advective equation. In the following section, CCMC provides another technique in finding find face values.

 For purely convective problems, as the case here, the solution of from the Eqn.(1) will read

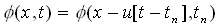
If the scalar versus position x is plotted at different time periods, the curve of will move along the characteristic direction with a convective speed u at different time steps. The west face of the i-th node of control volume is the face of interest and is denoted as . The variation of the versus time t can be plotted into a curve. This curve is called the convective characteristic curve. The convective characteristic curves for slope and curvature of can be construct in the similar way. These two curves provide a tool to construct the convective interpolation,, without phase angle shift. The details will be discussed in the following section. However, the over-shoot and under-shoot can be reduced by the consideration of the local behavior of the profile. This could be solved by the help of the normalized variable diagram and the 'limiter'.

There are three bench mark test problems examined in Leonard's . They are unit step function, sine-squared wave and semi-ellipse function. These are selected on the basis of simplicity and ease of reproducibility, and are intended to represent basic characteristics of behavior that might be encountered in practice. Finally, the results obtained from the proposed method, characteristic convective with monotonic conservation, are compared with those results presented in Leonard's , CDS, UDS, and MUSCL. Overall performance is slightly better than the MUSCL at the smaller Courant number. This technique gives sharp results for the step simulation at all Courant numbers. It also generates a degree of artificial stair-casing for sine-squared and semi-ellipse simulation at all Courant numbers.

1. Roe (1985). Some Contributions to the Modelling of Discontinuous Flows. In E. Engquist, S. Odher, and R.J.C. Sommerville, editors, Proc. 1983 AMSSIAM Summer Seminar on Large Scale Computing in Fluid Mechanics, Lectures in Applied Mathematics., pages 163-193. Philadelphia, 1983. SIAN.
2. Roache. Computational Fluid Dynamics. Hermosa Publishers, Albuquerque, NM, 1972.
3. Leonard (1979). A Stable and Accurate Convective Modelling Procedures Based on Quadratic Upstream Interpolation. Comp. Math. Appl. Mech. Engng., 19:59-98, 1979.
4. Van Leer (1977) Towards the Ultimate Conservative Difference Scheme. V. A Second Sequel to Godunov's Method. J. Comput. Phys., 32:101-136, 1979.
5. Leonard (1991). The ULTIMATE Conservative Difference Scheme Applied to Unsteady One-Dimensional Advection,. Computer Methods in Applied Mechanics and Engineering, 88:17-74, 1991.

ABSTRACT 

We consider the mathematical model for an adiabatic tubular chemical reactor which processes an irreversible exothermic chemical reaction. For steady state solutions, the model can be reduced to the ordinary differential equation

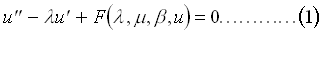
with boundary conditions

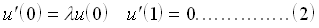
 where

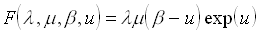
(see [1]). The unknown represents the steady state temperature of the reaction, and the parameters , and represent the Peclet Number, the Damkohler Number and the dimensionless adiabatic temperature rise respectively. This problem has been studied by numerous authors (e.g. [1], [2], [3]) who have demonstrated numerically the existence of solutions (sometimes multiple solutions), for particular parameter ranges.

In order to develop general results concerning the solution of (1)-(2), we convert the problem into an Hammerstein integral equation  

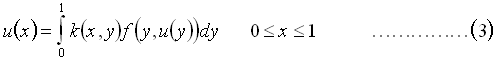
where is defined by

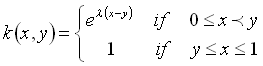
and 

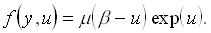
Existence and uniqueness results are achieved for specific ranges of the parameter .

Our main concern is to consider the application of a novel numerical procedure known as Adomian's Method to approximate this unique solution. It has been claimed that this method is particularly well suited for the solution of Hammerstein integral equations ([4]). An advantage of this method is that it produces an analytic approximation to the solution, i.e. a function defined on [0,1] , rather than approximate numerical values at a discrete set of points.

Adomian's method is used for solving solving operator equations of the form  

where is a nonlinear mapping from a Banach space into itself and is known. It is assumed that and can be expanded as infinite series  

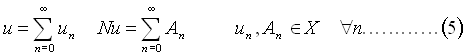
Here, , are the so-called Adomian's polynomials, (although, as we demonstrate, they are not always polynomials). depends on . By setting 

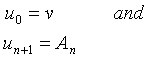
*we formally solve (4), and have an iterative procedure allows the successive calculation of , .

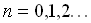This method is applied to the Hammerstein integral equation (3) in two cases: (i) and (ii) b = 0 . In the first case the method appear to converge rapidly, (although no convincing proof of convergence is known to us) and in the latter case the method gives the known unique trivial solution.

The solutions achieved in case (i) using Adomian's method is compared with numerical solutions achieved by application of the Contraction Mapping Principle and by using a simple shooting method applied to the original boundary value problem (1)-(2). For all calculations, the Computer Algebra Software, Maple, is used. Good agreement between the results of Adomian's method and the other methods is demonstrated. Since the Contraction Mapping Principle gives an iteration procedure which is known to converge to the unique solution, this strongly suggests that Adomian's method converges to the unique solution in this case.

References

1. Poore, A.B. A Tubular Chemical Reactor Model. A Collection of Nonlinear Model Problems Contributed to the Proceeding of the AMS-SIAM. p28-31, 1989.
2. Heinemann, R. Poore, A. Multiplicity, Stability, and Oscillatory Dynamics of the Tubular Reactor. Chemical Engineering Science. 36, 1411-1419. 1981.
3. Heinemann, R. Poore, A. The Effect of Activation Energy on Tubular Reactor Multiplicity. Chemical Engineering Science. 37, 128-131. 1982.
4. Some, B. Some Recent Numerical Methods for Solving Nonlinear Hammerstein Integral Equations. Mathematical Computer Modelling. 18, 55-62. 1993.

COMPUTATION OF TRANSIENT BUOYANCY DRIVEN FLOWS USING A FINITE ELEMENT PROJECTION TECHNIQUE

R.L. Sani* and D. Veyret**
*Dept. of Chemical Engineering, University of Colorado,
Boulder, CO 80309-0424 USA
** I.U.S.T.I., Université de Provence
5, rue Enrico Fermi 13453 Marseille cedex 13 France

A Galerkin finite element projection method for the numerical modeling of transient buoyancy driven flows is presented. Time accurate solutions are obtained by using a semi-consistent mass projection algorithm which is shown to have better phase speed accuracy than similar finite difference or lumped mass finite element algorithms. Its accuracy is discussed and validated by comparison of numerical experiments with an exact solution.

The mathematical model used for the system is the coupled linear momentum and energy equations employing the Boussinesq approximation.

plus appropriate boundary and initial conditions.

The basis of the finite element based algorithm is the use of a projection method to approximate the solution of the Boussinesq equations. One rewrites the equations in the form:

plus appropriate boundary and initial conditions where

Then one can interpret the solution of the system in the following manner: given u, the vector F(u,T) is known and can be projected on to the subspace of solenoidal vectors and the subspace of curl-free vectors , i.e.,

where P is a projection operator. This viewpoint is equivalent to restricting the solution of the equations to the space of solenoidal velocity vectors. The scheme utilized in the finite element algorithm is an approximation wherein one utilizes an approximation to , for example, and computes the intermediate velocity field from

then projects onto the space of solenoidal vectors via

and then accepts v as the solution at the current time. While this description contains the essential features of the scheme, the actual scheme must address such issues as the appropriate boundary conditions for and the appropriate form of .

A Galerkin finite element spatial discretization coupled with a semi-implicit temporal discretization is used to discretize the equations. The noteworthy features are that only a sequence of uncoupled, symmetric, positive definite algebraic systems must be solved for the temperature field and each velocity component and a discrete Poisson equation for the projection and update. Thus, this forms the basis of an efficient scheme which is amenable to the implementation of iterative solution techniques. Another noteworthy feature is that the consistent mass matrices have been in the discretized linear momentum and energy equations. This leads to an increased phase accuracy which is essential for accurate modeling of convectively dominated flows and concomitant thermal transport.

Some numerical experiments validating the temporal accuracy of the scheme as well as the numerical modeling of some complex 2D and 3D transient buoyancy driven flows will be presented.

ON THE INTEGRAL TRANSFORM SOLUTION OF THE HEAT DIFFUSION EQUATION IN A SLAB WITH RADIANT FLUX AT THE OUTER SURFACE

A. G. Oliveira Filho. * and C. M. Hackenberg. **
* Military Institute of Engineering (IME), Chem. Eng. Dept.,
Praça Gen. Tiburcio 80, 22290-270-Rio de Janeiro-RJ, Brazil.
** PEQ/COPPE/UFRJ, Chem. Eng. Dept.,
P.O. Box 68502, 21945-970-Rio de Janeiro-RJ, Brazil.

ABSTRACT

In this work, some known solutions of the transient heat transfer equation in a slab with thermal radiation are reviewed. One notices that the traditional way to deal with this kind of problem is to obtain a lumped parameter transport equation from thermal energy flux balance at the body's surface and to include global radiation as one of its terms. Boundary conditions are either constant or homogeneous and the transient temperature profile is thereafter obtained through integration.

Although many applications are found in the literature that utilize these classical solutions, they will not provide accurate resuits in high temperature processes, such as in elevated pressure combustion chambers. Lumped analysis is not possible due to Biot Number limitations when diffusive transient behaviour plays an important role inside the solid.

Here, the diffusion equation in a solid slab is analitically solved with radiant flux at the outer boundary by the Integral Transform Technique and also by a functional method that uses the Basset-Duhamel Theorem for arbitrary boundary value problems. Thus, treating the surface temperature as an arbitrary function of time, the problem may be solved through computational codes. It's important to point out that the Integral Transform Technique generates a Sturm-Liouville problem whose eigenvalues and eigenfunctions are calculated by computation.

In a first step, the outer surface temperature function is solved utilizing a linearized form of the boundary condition. The non-linear boundary condition is also analyzed and the solution is then worked out through a first order approximation of the resulting functional integral equation at the outer surface. It is shown that the solutions converge to the existing lumped parameter solutions for highly thermal conductive materials, as expected. Hence, the procedure developed here is general enough to include all ranges of Biot Numbers.

Media composed of double-periodic phases with different (arbitrary) conductivity are ñonsidered. Within each phase temperature is a harmonic function and along interfaces two conjugation conditions hold (continuity of temperature and normal flux component) as well as periodicity conditions along the boundaries of elementary cells. For specific examples of composites (chequer-board, regular triangles, rectangular inclusions) explicit analytic solutions are derived in terms of the thermogradients. For other cases standard FDM procedures in terms of temperature are used and compared with analytic formulae. Bulk values of the field (total dissipation, effective conductivity) are calculated and compared with the approximate results of Rayleigh, Wiener, Odelevskii, Dul'nev and Zarichnjak, Bakhvalov and Panasenko. For the chequer-board composite the hodograph of effective conductivity is shown to coincide exactly with an ellipse while effective resistivity is a curve inversely symmetric with this ellipse about a circle. For the case of quadrangular inclusions, and for the specific case of a field oriented along one of the sides, the value of effective conductivity is shown to vary from to 1 /.

As limiting cases of parquets, the temperature fields are studied above the cooling surfaces. For the case of ideally conducting walls periodic fingers of optimal dissipation potential are derived and shown to coincide with the classical contours of Polubarinova-Kochina. In the class of semi-elliptic protrusions with an arbitrary conductivity ratio of the wall and environment, two non-trivial local extrema of total flux exist alongside two global ones. Rectangular fingers are shown to exhibit intuitively obvious behaviour at the large scale but less trivial field distribution exist near these tips. Another limiting pattern derived from the chequer-board composite is a fault in the standard layering. This defect is shown to provide more intensive conduction in one area of the composite and less intensive in others. For isolated inclusions in homogeneous matrixes (which model caverns or macropores) the non-trivial interaction between two neighboring cavities is studied. For the case of heat dissipation from a wall underlying flow of a viscous fluid the Couette-type regime is considered, and optimal riblets are established. Shape optimization is performed for inclusions placed in 2-D flows with the corresponding total heat flux depending on the Peclet number. 

1. Kacimov, A.R. Optimization of the protrusion shape for a Couette type flow, Optimal Control Applications and Methods, Vol. 15, pp 93-203, 1994.
2. Kacimov, A.R., and Obnosov ,Yu.V., Explicit, rigorous solutions to 2-D heat transfer: Two- component media and optimization of cooling fins, International J. Heat and Mass Transfer, Vol. 40, pp 1191-1196, 1997.
3. Kasimov, A.R., and Obnosov, Yu.V. Explicit solutions to problems of shape and regime optimization in steady heat transfer, Proceedings of I Russian Natl. Conference in Heat Transfer, Moscow, Vol.8, pp 91-96, 1994.
4. Obnosov ,Yu.V., Solution of a Markushevitch problem in the class of doubly-periodic functions with orthogonal periods. Sov.Phys.Dokl., Vol. 36, pp 73-74, 1991.
5. Obnosov , Yu.V., Solution of a problem of R-linear conjugation for a triangular regular checkerboard field, Sov.Phys.Dokl., Vol. 37, pp 46-48, 1992.
6. Obnosov ,Yu.V., Exact solution of a problem of R-linear conjugation for a rectangular checkerboard field. Proc. Royal Soc. London A, Vol.452, pp 2423-2442, 1996.

VERIFICATION OF TEMPERATURE PROFILES IN POROUS MEDIA WITH EXPERIMENTAL DATA

S. S. Helvacý, S. Yapar

Abstract is not available.

Among the fire retardant systems¹ there exist a peculiar class - so-called "intumescent systems", which posses the property to produce on their surface under conditions of external heat flow protective coke layer - foamed char (FC)². This layer can be tens times thicker than initial coating and protect polymer from the external influence. Practically all authors, who investigate behaviour of intumescent systems, agree that heat-protective function of FC is one of the main factors which explain great efficiency of intumescent coatings. Moreover, it has been shown³ that efficiency of the intumescent fire retardant system correlate with the thermoprotection properties of foamed char.

There exist a number of works devoted to numerical simulation on intumescent system burning^4-7 and investigation of thermal conductivity of foamed char layer^8-9. However practically in all existing works foamed char cap was considered as a uniform medium. But it is known that radiation can play a significant role and affect on the heat transfer processes in porous media⁹. So we need in mathematical model of heat transfer in foamed chars which can accurately takes into consideration as all mechanisms of heat transfer (conduction, radiation etc.) as well as influence of external factors - heat losses through substrate, external heat flow and so on. The aim of present work is to present three-dimensional model of heat transfer into porous media at high temperatures and conduct some analysis of contribution of each heat transfer mechanisms into total heat flux. 

Thermo-protection properties (TPP) of FC the was investigated by the following method. The sample (char plate 3-7 cm thickness) was placed on the asbestos table. Up surface was subjected by the continuous heat flow from CO₂-laser (10.6 nm wavelength, 5 W/cm² power of the beam). The responce of the thermocouple (Pt - Pt+10%Rh, 50 mkm wire diameter), located on the back side of the sample, vs. time was registered. 

Theoretical model

FC was considered as a porous medium. Total volume was separated on the cube "element cells". The edge length of each cell was 10^-2 mm. It was Each cell can be either empty or filled by char material. The initial distribution of filled cells was made in accordance with integral foamed char characteristics - their effective density, average pores diameters, etc. Pores with fixed diameter d₀ were distributed in the model char cap in random order. Vertical cut of the model char cap presented on the fig. 1.

Heat transfer was computed in the follows way. If two filled cells are separated by some (one or more) empty then heat flow between them will be

,

where l _aer - heat conductivity of the air, n - number of empty cells, T_i - temperatures of the cells, e - blackness coefficient of the char, s - Stefan-Boltzman constant.

In the case of contacted filled cells, their heat exchange will be

,

where l _c - heat conductivity of the char material.

For the cells, located on the up surface external heat flow Q will give their addition to the heat flow to the cell. For these cells heat flux from the up side will be the next:

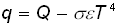
Note, that in this expression external heat flow supposed to be recalculated on the cell facet area, i.e. d₀².

The lowest layer, which contact with substrate supposed totally filled. In the expression of heat flow to this layer we need to introduce the member, which will describe heat losses through substrate. In present model this member was written in the follows manner:

,

where g is the coefficient of heat losses, T₀ - environmental temperature.

For the each time step cells temperatures was computed. Than in accordance with above equations we can compute total heat flux to the each cell and from these data we can compute new cells temperatures. Initial distribution of temperatures was supposed stationary and for each cell equal to T₀. Time interval in calculations was 10^-2 s.

In such model the average temperature on the lowest layer will represent the response of thermocouple, located on the back side of the sample. In further discussion as TPP we'll use the maximal temperature of this layer. The char in the model is considered as indestructible - it provide existence of this temperature. 

In order to compare experimental and theoretical results TPP of real intumescent system on the base of carbamide-formaldehyde resin with intumescent addition (PER+APP) have been investigated. This systems is notable for the uniform foamed char, which it produce during burning. Comparison of the experimental and theoretical data indicates that supposed model provide good agreement with experiment. All calculations were made on the base of real char characteristics.

In order to study heat transfer in foamed chars we should answer some questions. First, we need to know the influence of FC structure on their TPP. Secondly, the role of substrate heat conductivity should be examined. And the last - we have to know the contribution of each heat transfer mechanism (radiation, conduction, etc.) to the total heat flux. When we'll be able to answer all these questions we'll can to conclude that we know all features of heat transfer in FC. Some aspects of these questions already have been discussed in detail⁹.

First of all let us study the influence of char structure on their TPP (maximum temperature of the last layer). From the analysis it can be seen the decreasing of pore diameters lead to decreasing of back side temperature. It should be noted here that contents of air in FC was supposed more than 70%, this point has been previously examined¹⁰. Behaviour of described dependence shows us one important aspect of heat transfer - radiation play a significant role. Indeed, if we separate two heated plate by third (with intermediate temperature), it will lead to decreasing of radiation flow, but the conductive flow remain practically unchanged. Increasing of FC cap height lead to decreasing of back side temperature. In first rough approximation we can speak about liner dependence of back side temperature vs. char cap height and average pores diameter.

Some words about influence of substrate. In order to take it into account we introduced in our model coefficient of heat losses through substrate g . In fact this term represent thermal conductivity of the substrate. From the examination of temperature response for equivalent char caps on different substrates we can conclude that in first approximation value T-T₀ is reverse proportional to the g . On the base of this expression we can estimate efficiency of the intumescent coating on any substrate in the case when we know it for any particular substrate.

1. Aseeva, R.M. and Zaikov, G.E., Combustion of polymeric materials, Nauka, Moscow, 1981
2. Camino, G., Costa, L., Martinasso, G., Intumescent Fire-retardant Systems, Polymer Degrad. and Stab., Vol. 23, pp. 359-376, 1989
3. Reshetnikov, I., Antonov, A., Rudakova, T., et al., Some aspects of intumescent fire retardant systems, Polymer Degrad. and Stab., Vol. 54, pp. 137-141, 1996
4. Gibov, K.M., Zhubanov, B.A., Dovlichihin, T.H., et al., About fire retardation mechanism of intumescent paints, Proceedings of Int. conf. "Nehorlavast Polymernych Materiolov", Bratislava, 1976, pp. 69-71
5. Buckmaster, J., Anderson, C., Nachman, A., A Model for Intumescent Paints, Int. J. Eng. Sci., Vol. 24, No. 3, pp. 263-276, 1986
6. Zverev, V.G., Isakov, G.N., Nesmelov, V.V., et al., Heat Transfer Mechanism and Fire Insulation Properties of Some Intumescent Materials, J. of Polym. Mat., Vol. 20, No. 1-2, pp. 91-101, 1993
7. Butler, K., Baum, H., Kashiwagi, T., Three-Dimensional Modeling of Intumescent Behavior in Fires, Proceedings of 5^th Int. Symp. on Fire Saf. Sci., Melbourne, 1997
8. Anderson, C.E., Ketchum, D.E., Mountain, W.P., Thermal Conductivity of Intumescent Chars, J. of Fire Sci., Vol. 6, pp. 390-410, 1988
9. Reshetnikov, I.S., Khalturinskij, N.A., About modelling of intumescent systems burning, Russian Journal Chem. Phys., Vol. 16, No. 2, pp. 102-107, 1997
10. Gnedin, Ye., Kozlova, N. et al. Structure of foam cokes formed in pyrolysis and burning of polymers containing foaming fire-retardant systems, Vysokomolek. Soed., Vol. 33(A), pp. 1568-1575, 1991
11. Kanary, K., Heat conductivity of high polymers, Denki sikinse hose daigaku, Vol. 176, 1973 

The work reported in this paper is concerned with the moisture migration process that causes drying of the soil involving buried electrical power cables. Numerical simulations have been performed for periodic and non-periodic geometries, and for two types of soils: one natural and other artificial. The results showed that, for initial times, the two geometries give very similar temperature and moisture content profiles in the vicinity of the cable. It was also observed that for the natural soil used the drying process is more intense than for the artificial soil. 

The study of simultaneous heat and mass transfer processes in soils is of great interest in different engineering and environmental applications. The work reported in this paper is mainly concerned with the heat and mass transfer process that occurs in soils that involve underground electrical power cables. The electrical current passing through these cables generates heat which has to be dissipated by the surrounding soil in order to keep the cable temperature at an acceptable level. The heat generated and dissipated by the cable induces a moisture migration in the soil surrounding it. This, in turn, increases the thermal resistance of the soil which starts to behave as a thermal insulator. As a consequence, the temperature at the surface of the cable can reach values which are higher than the maximum operating level, causing damage, and even rupture, of the cable. Considering the high costs involved in buried power cable systems, it is of interest to understand and to predict the behavior of the moisture front migration in the surrounding soil. In this work, two types of soils, one natural and other artificial (backfill), and two distinct geometries, one periodic and other non-periodic, were investigated. The main objective was to compare the behavior of the temperature and moisture content profiles for the two geometries studied.

The governing equations of the problem are the energy and moisture content transport equations, which for unsaturated porous media can be written as¹:

(1)

(2)

where T is temperature and q is the volumetric moisture content (ratio between the liquid volume and the total volume of the medium); t is time and x and y are the spatial coordinates; C is the volumetric heat capacity; k_* is the soil apparent thermal conductivity; r is the density of the liquid; h_lv is the latent heat of vaporization; DTv and Dq v are the difusivities of the vapor associated with the temperature and moisture content gradients, respectively; DTl and Dq l are the difusivities of the liquid associated with the temperature and moisture content gradients, respectively; and KH is the hydraulic conductivity of the porous media. These governing equations are based on the Philip and De Vries model² . The physical properties and diffusivities were considered to vary with both temperature and moisture content of the porous material. In this work, the expressions used for the computation of these properties were obtained experimentally by Hartley et al.³

For simplicity, only cables with square cross section were considered. The geometries of interest are schematically represented in Figs. 1(a) and (b). For the periodic situation (Fig. 1 (a)), the calculation domain was restricted to a single cable, with cyclic conditions applied along lines A-B and C-D. Fig. 1 (b) represents the non-periodic situation with three cables buried. For this case, due to symmetry along line E-F, only half of the geometry was included in the calculation domain. The surface of the cable is impermeable to mass flux and is maintained at a constant temperature T_c. Other boundary conditions can be seen in Figs. 1 (a) and (b). Initially the soil is at a uniform temperature T_i and uniform moisture content q _i. Two initial values of q _i, representing intermediate and practically saturated soils, were analyzed. Results are presented in terms of moisture content isocurves, and nondimensional temperature and moisture content profiles for different stages in time and for the two geometries considered.

The governing equations were discretized using a Finite Volume Method with the fully implicit scheme for time discretization. Computations were performed with nonuniform grids and varying time steps. Two line-by-line iterative algorithms were used to solve the set of governing equations: The tridiagonal and cyclic tridiagonal matrix algorithms (TDMA and CTDMA). The cyclic algorithm is required for lines of nodes along which the periodic boundary conditions apply. At each time step, convergence of the iterative solution procedure was assumed when the sum of the absolute values of the residues of the governing equations were less than 10^-8.

Fig. 2 shows a comparison of the moisture migration front (along a vertical line passing through the center of the cable) for the case of the native soil with an intermediate initial moisture content (q _i = 0.15), and the periodic and non-periodic geometries studied. Immediately close to the cable, and for all times, the moisture content always presents the smallest values due to the high temperature and the heat dissipated by the cable. For initial times (2.4 hours), it is observed an increase of the moisture content above the initial value in the region nearby the cable. This is because, at the beginning of the process, the water present in the soil close to the cable evaporates and starts to migrate. Eventually, this vapor encounters colder regions and condenses, thus increasing the moisture content of that particular region. For longer periods of time (300 hours), the increase of the moisture content above the initial value, occurs in regions further away from the cable. It is also observed in Fig. 2 that, initially, the two geometries present practically the same moisture profiles. However, as time evolves, the periodic geometry presents slightly higher levels of moisture content in the adjacent vicinity of the cables. This happens because, in reality, the periodic geometry represents a situation of several cables buried in an in-line arrangement, rather than the three cables represented by the non-periodic geometry. Thus, it would be expected that with the periodic conditions imposed, the moisture content would be somewhat higher in the cable surroundings.

A numerical investigation of the drying process that occurs in soils in the neighborhood of buried power cables considering periodic and non-periodic geometries has been presented. The results have shown that, for initial times, the two geometries give very similar temperature and moisture content profiles. However, as time is advanced, the periodic geometry gives rise to higher temperature and moisture content of the soil in the neighborhood region of the cables. It was also observed that for the natural soil used, the drying process is more intense than for the artificial soil or backfill.

The authors wish to thank the support of the Brazilian government (CNPq) and the Research Foundation of Rio Grande do Sul (FAPERGS).

1. Damasceno Ferreira, L.S., Heat Transfer and Moisture Content Migration in Soils Surrounding Buried Power Cables, Ph.D. Thesis, Mech. Eng. Dept., UFSC, Brazil, 1993 (in Portuguese).
2. Philip, J.R., De Vries, D.A. , Water Movement in Porous Media under Temperature Gradients, Trans. American Geophysics Union, Vol. 29, pp. 222-232, 957.
3. Hartley, J.G., Black, W., Bush, R.A., Martin Jr, M.A., Thermal Stability of Soils Adjacent to Underground Transmission Power Cables, Technical Report, Georgia Institute of Technology, 1982.

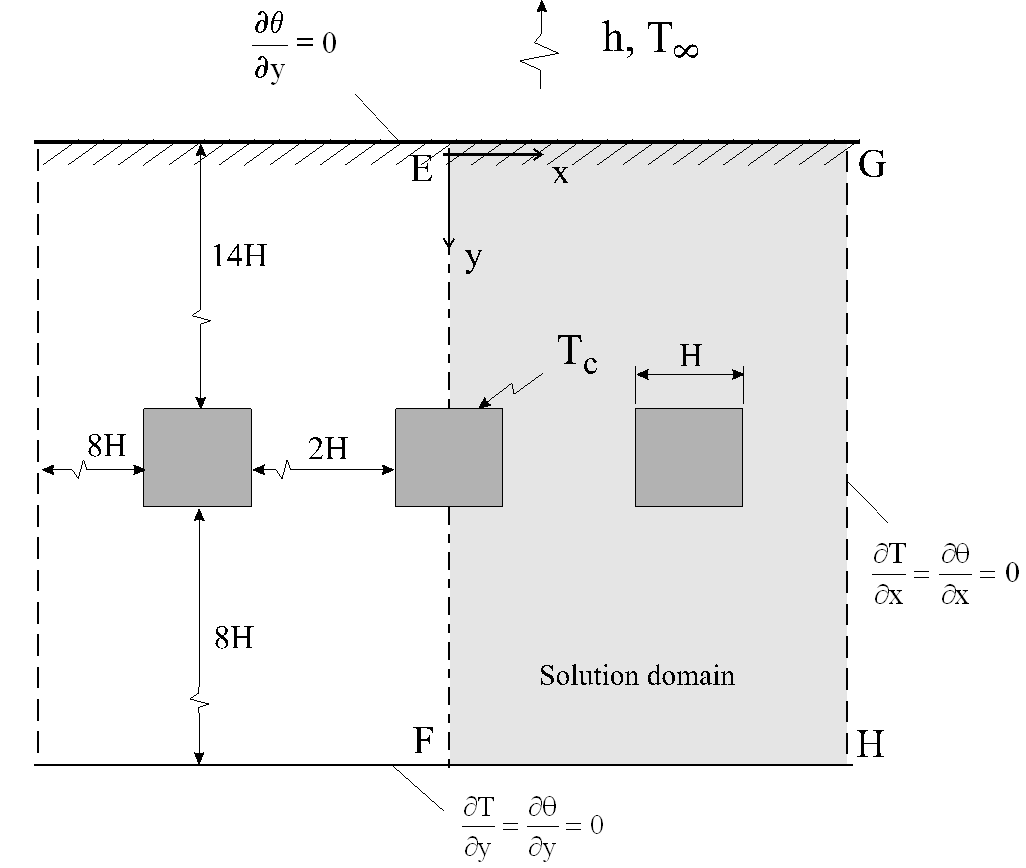
Fig. 1 - Geometries investigated (not to scale): (a) periodic, and (b) non periodic.

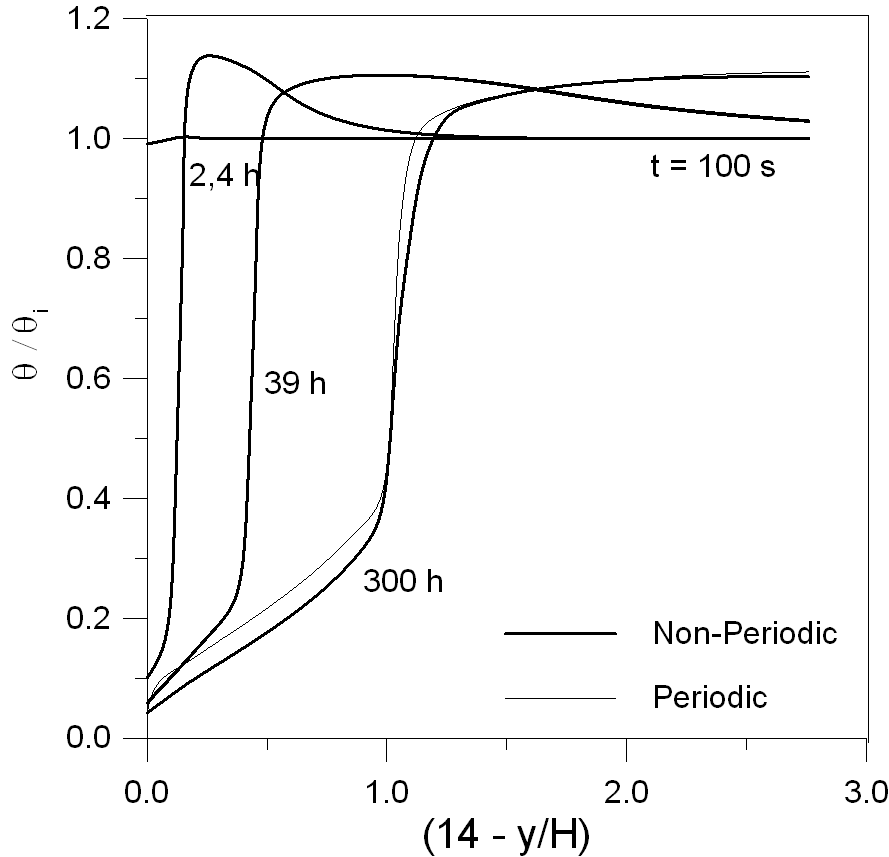
Fig. 2 - Moisture migration front along the y coordinate.

A STUDY ON THE BOUNDARY ELEMENT SOLUTION OF HEAT CONDUCTION PROBLEMS

Ý. Ekmekçi, N. Sözbir, Ü. Uysal, Ý. Çallý
Department of Mechanical Engineering, Sakarya University, Sakarya, Turkiye

ABSTRACT- This paper is concerned with the numerical solution of two dimensional steady state heat conduction problems with Boundary Element Method. In order to obtain an approximated solution of a boundary value problem with Boundary Element Method, influence type functions which are called fundamental solutions are used as weighing functionsand in this manner, approximate solution is fully satisfy our governing equation in the domain exactly, while this approximated solution is being forced to satisfy weighted integral on the boundary. The development of the method is generalized to include the first, second and third kind of boundary conditions as well as non-linear radiation conditions. A variety of illustrative problems are analyzedwith this method and their solutions are compared to those obtained analytically. The solutions for the examples indicate that the Boundary Element Method is very efficient and accurate for solving most of the condition problems. This method has no inherent limitations such as the geometric complexity, kind of boundary conditions. As in most of the practical calculations of heat transfer, boundary fluxes and temperatures are only needed informations. However complete temperature distribution can be directly obtained with minimum effort.

A NEW ALGORITHM FOR THE SOLUTION OF HEAT CONDUCTION PROBLEMS WITH THE FINITE DIFFERENCE METHOD

H. Ý. Saraç* , N. Sözbir**, Ý. Ekmekçi**, Ü. Uysal**, Ý. Çallý**
* Department of Mechanical Engineering,
Kocaeli University, Kocaeli, Turkiye
** Department of Mechanical Engineering,
Sakarya University, Sakarya, Turkiye

ABSTRACT- In this paper, a new application of solving systems of linear equations obtained by applying the finite-difference method to two-dimensional steady state conduction problems is proposed. This proposed new algorithm is composed of three steps: (i) transformation of the original system to an auxiliary linear system, (ii) solution of this auxiliary system by Gauss-Siedel iteration method, and (iii) determination of the roots of original system using the solution vector of the auxiliary linear system.