Session 1

Chairman: G. de Vahl Davis

With the growing capacity of computers and continuing improvement in numerical codes, the question of the exactness of numerical solutions to describe real fluid flow is of primary importance. Often results from idealised models, limited only to global description in terms of non-dimensional flow and heat flux characteristics, are accepted and successfully applied in engineering applications. However, there is a wide class of practical problems where knowledge of just the general behaviour of flow is not sufficient to obtain a full quantitative explanation of the phenomena. Examples include the distribution of fuel or soot in a combustion chamber, the transport of impurities in crystal growth, and the propagation of pollution in air and water. In such cases the knowledge of some specific flow details is necessary for the full control of the investigated phenomenon. Improvement in the accuracy of theoretical and numerical models and their validation using experimental data become the necessary steps to solve such problems.

For the thermally driven flow the velocity and temperature fields are primary quantities that characterise a given flow. In the past, the point measurements were preferred to validate numerical codes. Despite the high accuracy characterising point methods (e.g. Laser Doppler Anemometry), limited number of simultaneously acquired values makes their use for the validation procedure potentially questionable. Therefore, we firmly believe that 2-D or 3-D flow field acquisition methods are the only alternative, especially for transient phenomena. With this objective in view new experimental techniques were developed by the author and his co-workers and applied to the study of heat and mass transfer problems in flow of liquids.

The primary method is based on a computational analysis of the colour and displacement of liquid crystal tracers¹, and it is used to determine both the temperature and velocity fields of the flow. It combines Digital Particle Image Thermometry (DPIT) and Digital Particle Image Velocimetry (DPIV). Full 2-D temperature and velocity fields are determined from a pair of colour images taken for the selected cross-section of the flow. Furthermore, a 3-D flow structure can be reconstructed from a few sequential measurements, if the flow relaxation time is sufficiently long.

In some cases even apparently good agreement of measured and calculated velocity and temperature fields does not guarantee their equivalence. The residual discrepancies may result in evidently different flow patterns. Detection of these differences in not an easy task. For this purpose the second experimental method was introduced: automatic 3-D tracking of single tracer particles suspended in the flow medium. Due to the strong sensitivity of the particle position to small additional forces or numerical inaccuracy, it could be demonstrated that observed and simulated trajectories are often far from being in acceptable agreement, even for well known standard problems. In several cases experimentally simpler 2-D particle tracking was found useful to demonstrate basic differences between observed and calculated flow patterns.

One of the main sources of observed differences is the three dimensional character of the flow which complicates its numerical modelling. The thermal boundary conditions (TBC) taken at non-isothermal walls are in practice neither perfectly adiabatic, nor perfectly heat conducting, as is usually assumed in numerical models. In addition, the widely used Boussinesq approximation for the physical determination of the fluid flow is not strictly valid for real fluids. In particular, dependence of viscosity on temperature for such liquids as glycerine or oils may generate severe discrepancies between expected and observed flow patterns.

In this paper our attempts to understand and explain observed discrepancies between measured and calculated convective flow patterns are reviewed for three investigated topics on natural convection: differentially heated cavity, lid-cooled cavity and natural convection with phase change (freezing of water). To compare experimental results numerical simulations of transient and steady states were performed using numerical codes developed by the CFD group at News South Wales University (G. de Vahl Davis, E. Leonardi and G. Yeoh). The velocity-vector potential finite difference formulation of 3-D Navier-Stokes was used. These computational models were adopted to simulate as closely as possible the physical experiment. Specifically, either the heat flux through the non-isothermal walls was computed to match the measured wall temperature, or the measured values of the temperature of the walls were used in the calculations. Furthermore, the coupled solid-fluid heat conduction problem including bounding walls was solved together with momentum equation to improve modelling of the physical experiment. The effect of variable fluid properties on the resulting simulation was checked.

The first study concerns a popular „bench mark” case, low Rayleigh number natural convection (Ra=20.000-100.000) in a cubical cavity with differentially heated end walls^2-3. Two opposite vertical walls are isothermal, the other four walls are nominally insulators of finite thermal diffusivity. A heat flux both through and along the walls is generated due to temperature gradients existing between the fluid inside the cavity and the surrounding atmosphere and also along the front and back walls, the lid and the floor of the box.

The main flow structure consists of one or two spiralling motions, responsible not only for recirculation of the liquid from the hot to the cold wall, but also for „cross-flow” from the side walls to the cavity center and back. The 2-D flow pattern observed in the centre symmetry plane can be well reproduced numerically. However, severe discrepancies appeared when 3-D structures were compared. It soon became obvious that the 3-D flow structure depends very sensitively on the thermal properties of the four non-isothermal walls. Depending on modelled conditions splitting of the spiralling structures, changing their pitch and even reversing direction was obtained. By imposing measured values for the side walls temperature fields, as new boundary conditions in the numerical code, it was possible to obtain good agreement.

In the second example investigated, the top wall of the cube is isothermal at low temperature, whereas the other five walls are non-adiabatic, allowing a heat flux from the external fluid surrounding the box. The temperature of the external bath is kept constant. Due to forced convection in the bath it can be assumed that the temperature at the external surfaces of the box is constant and equals the bath temperature. The temperature field at the inner surfaces of the walls adjusts itself depending on both the flow inside the box and the heat flux through and along the walls. This configuration was selected to investigate convective flow with and without a phase change (freezing of water at the top wall) ⁴. To some extent it resembles a vertical Bridgman configuration used for crystal growth.

Natural convection in the cavity with a cooled top wall exhibits a complex character. Physically this configuration has some similarity to the Rayleigh-Bé nard problem. However, due to the different thermal boundary conditions at the side walls, the flow structure is different. The cubic symmetry of the box imposes a strong downward flow along the vertical axis of symmetry. However, before this stable final flow structure is achieved, several dramatic changes in its pattern are observed. The final stable configuration consists of eight symmetrical flow cells with spiralling structures transporting fluid up along the side walls and down in a central cold „jet” along the cavity axis. Comparison of numerical and experimental results for the centre plane of symmetry indicated some minor discrepancies in the temperature and velocity fields. Serious discrepancies were noticed for temperature distribution observed for the horizontal cross sections. It indicated, that the physically realised 3-D flow structure is different from the predicted one. Closer investigations showed that the thermal boundary conditions posed for the five non-isothermal walls were triggering different flow patterns, even if global flow conditions are apparently untouched. Physically it is possible for a flow pattern with two opposite sequences to develop. Either the flow spirals inwards in the central plane and outwards on the diagonal plane, or the other way around. Therefore only slight change in the thermal boundary conditions may easily modify the flow pattern. This was confirmed by replacing the side walls of low conductivity Plexiglas by thin glass walls.

The numerical simulations performed using the 3-D model for wall heat conductivity confirmed the triggering mechanism of TBC on the observed flow pattern. Inclusion of the side walls in the computational domain and solving the coupled fluid-solid heat conduction problem improved agreement with the observed flow pattern. Furthermore the observed temperature distribution as well as its symmetry were fully recovered in the numerical results.

If the phase change takes place at the cold wall, the complicated flow pattern which appears when convection starts, becomes visible in the „star-like” structure of the solidus (ice). The growing boundary interacts with the flow pattern passing through several asymmetrical forms. Hence, both ice structure and the flow pattern developed were initially strongly asymmetric, before asymptotic steady symmetrical configuration was recovered. Difficulties encountered to reproduce numerically both the transient and final states will be discussed. It was found, that the formulations of the thermal boundary conditions, as well as those of the initial flow conditions and the fluid properties need verification to achieve agreement with experimental data.

Our experience shows that solving complex problems may be eased when experimental feed back is present. In most cases, it was simplification of the thermal boundary conditions at apparently „unimportant” side walls, that was responsible for difficulties in numerical modelling. As a result of the use of both experimental and numerical methods the fine structures of the thermal flow were understood fully. This is because of the difficulties in predicting changes of the flow pattern, which are triggered by a minor modification of the thermal conditions at usually idealised „side walls”. It is however impractical and usually impossible to take into account all possible factors creating the „environment” of an investigated case. Properly planned experimental „bench-marks” may elucidate sensitiveness of the flow to such secondary flow conditions, that is otherwise hard to predict.

1. Hiller, W., Kowalewski, T.A., Simultaneous measurement of the temperature and velocity fields in thermal convective flows, Flow Visualisation IV, (Editor Claude Veret), pp. 617-622, Hemisphere, Paris 1987.
2. Hiller, W.J., Koch, St., Kowalewski, T.A., de Vahl Davis, G., Behnia, M., Experimental and numerical investigation of natural convection in a cube with two heated side walls, Proc.of IUTAM Symposium, Cambridge UK, Aug. 13-18, 1989, (Edits. H.K. Moffat & A. Tsinober), pp 717 - 726, CUP 1990.
3. Yarin, A., Kowalewski T.A., Hiller, W.J., Koch, W.J., Distribution of particles suspended in 3D laminar convection flow, Physics of Fluids 8, pp. 1130-1140, 1996.
4. Kowalewski, T. A. Cybulski A., Experimental and numerical investigations of natural convection in freezing water, Int. Con. on Heat Transfer with Change of Phase, Kielce (Poland), Dec. 8-10, 1996, in Mechanics vol. 61/2, pp. 7-16.

The purpose of this paper is to invite interested researchers to partake in a comparison exercise to compute convection of air in a cubical enclosure, which is heated differently at two vertical side walls.The determination of buoyancy-driven flow ant heat transfer in a cubical cavity is a simple model problem of considerable practical interests. The problem also provides an excellent test of numerical methods and computer codes being used for the calculation of viscous convective flows. For the basic laminar two-dimensional flows in an air-filled square cavity, benchmark numerical solution has been suggested by G. de Vahl Davis¹.

We invite contributions to the solution of three-dimensional flow of a Boussinesq fluid of Prandtl number 0.71 in an cubical cavity with Y-vertically upwards ². Assume that all components of the velocity are zero on all the boundaries, that the boundaries at Z=0 and Z=1 and at Y=0 and Y=1 are insulated, and that T=0 at X=0 and T=1 at X=1. Calculate the flow and thermal field for Rayleigh numbers 10 ⁴,10 ⁵, 10 ⁶.

The following results should be supplied:

average Nusselt number on hot wall;

isolines of local Nusselt numbers on hot wall;

maximum and minimum local Nusselt numbers on hot wall and its locations;

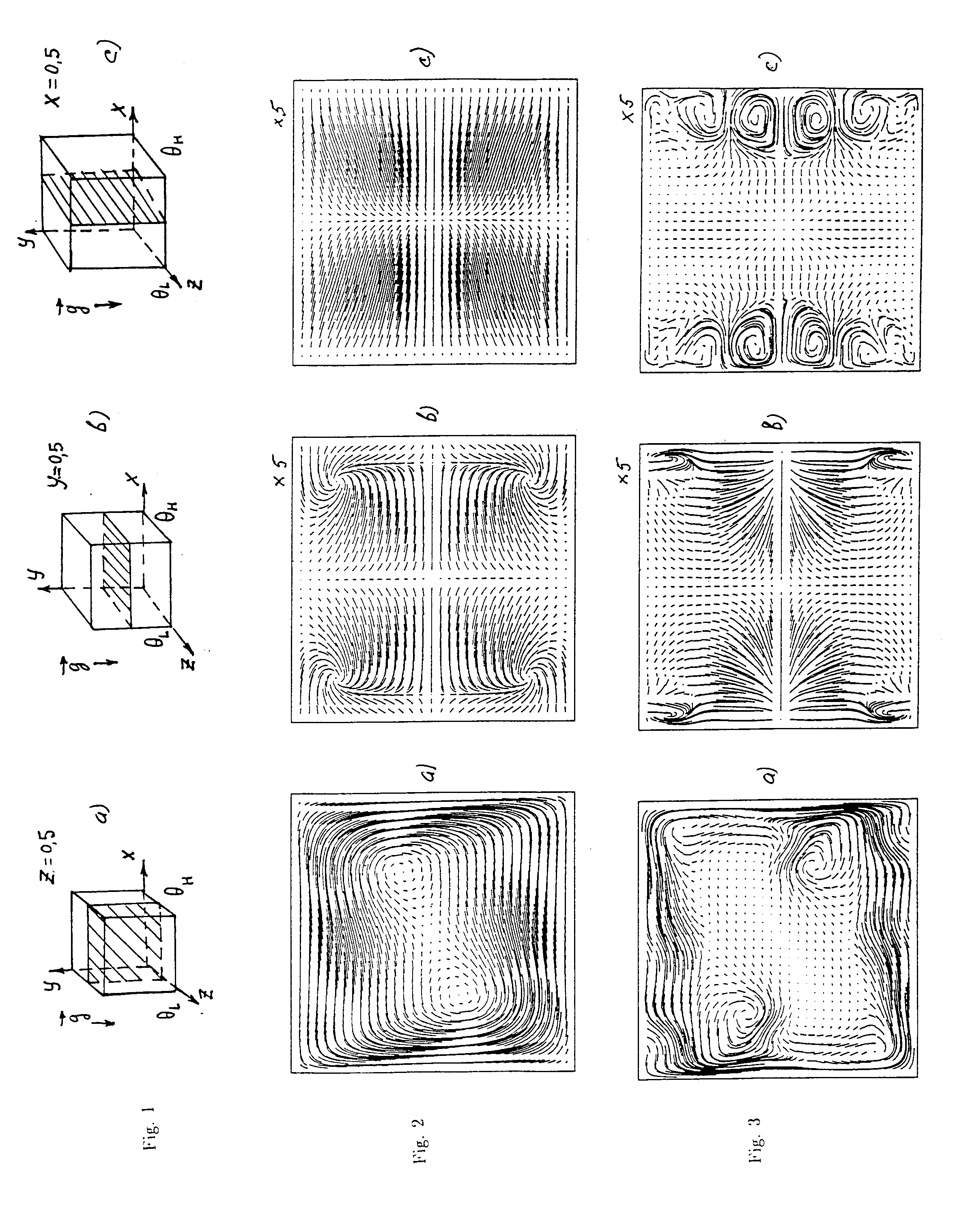
profiles of vertical Y-component of velocity V (X, Y=0.5) at vertical plane Z=0.5, fig.1a;

maximum this velocity and its location ;

profile of horizontal X-component of velocity V (Z, X=0.5) at horizontal plane Y=0.5, fig.1b;

maximum this velocity and its location;

profile of horizontal Z-component of velocity V(Y, Z=0.5) at vertical plane X=0.5, fig.1c;

maximum this velocity and its location;

isolines of temperature T at the vertical plane Z=0.5 and flow structure in three middle sections, represented at fig.1-- a,b,c;

In addition contribution should describe the method used and give relevant computational detail ( grid, computer, CPU time, storage etc.)

We use two codes -Scheme I for primitive and Scheme II for vorticity-potential function formulations of the governing equations on the base of Navier-Stokes equations in Boussinesq approximation. Explicit variant of the projection method was applied for the Scheme I³ . The main characteristics of Scheme II are the control volume formulation, regular non-uniform staggered grid, ADI, second order time integration. The codes have been tested using benchmark of driven 3D cavity for Reynolds numbers 400 to 3200⁴ and of the thermal gravitational convection in a cavity with differently heated vertical walls for four Ra numbers: 10⁴,10⁵, 10⁶, 8.6* 10⁶. The flow structures in three planes (fig.1-a,b,c,) are shown on fig.2-a,b,c for Ra= 10⁵ and instantaneous flow at t= 300 (nonstationary regime) on fig.3-a,b,c for Ra=8.6* 10⁶

.

For the steady state solution some comparison is done (Table 1). The comparison has been done using the following grids: 86 * 65 * 65 with reduced grid spacing near hot and cold walls (current work) and 62 * 62 * 62 nonuniform grid².

Table 1

Overall Nusselt Number on the heated wall

Fig.4--a,b,c demonstrates isolines of local Nusselt number on hot wall for three Rayleigh numbers 10⁴,10⁵, 10⁶ consequently.

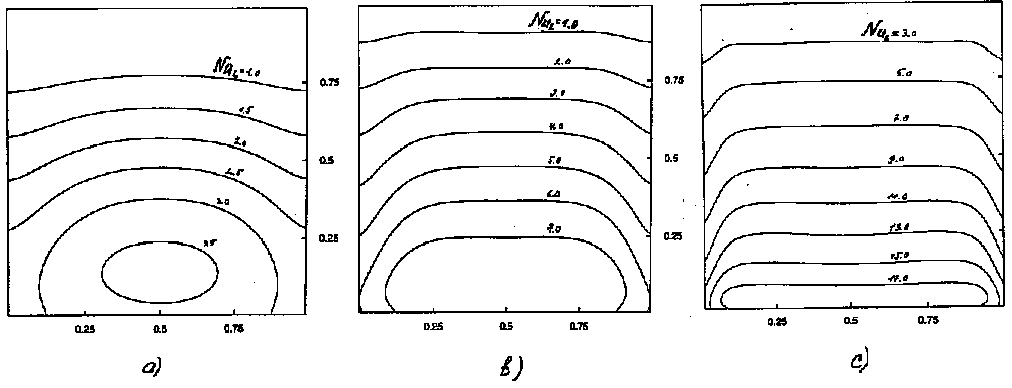
Fig.4

1. Davis G.de V. Natural convection of air in a square cavity: a bench mark numerical solution. Int. J. Numer. Meth. Fluids, vol.3, pp. 249-264, 1983.
2. Fusegi T., Hyin J.M. and Kuwahara K. A numerical study of 3D natural convection in a differently heated cubical enclosure. Int. J. Heat Mass Transfer, vol.34, pp. 1543-1557, 1991.
3. Nikitin S.A. Numerical investigation of 3D convection problems. Sci. Report, Inst. for Problems in Mech., RAS, 1989, 52p.
4. Bessonov O., Brailovskaya V., Polezhaev V. and Roux B. Lecture Notes in Computer Science, vol.964, pp. 385-399, 1995.

In recent years numerous experimental and numerical studies or analytical solutions, have been performed to explain the principal mechanism of energy transfer occurring during the melting or solidification. Application of numerical methods for freezing problem necessitate to solve non-linear partial differential equations of variable properties fluid coupled with moving solid/liquid interface. Due to the problem complexity, it is not a trivial task to determine precisely an error of the numerical results impeded by inevitable model simplifications. Hence, full field measurements of velocity and temperature gain their great importance. However, most of the available experimental data on freezing are limited to general observations of the phase change front and point measurements of the temperature.

Aim of the present investigation is to create an experimental benchmark for natural convection in freezing water. This benchmark consists of the interface position, temperature and velocity fields. An experimental investigation was performed for a 38 mm cubical box with four 6 mm thick Plexiglas walls. Two vertical opposite metal walls were differentially heated. The temperature of cold and hot wall was -10^oC and +10^oC, respectively. Distillate water was selected as a flow medium for its well known thermophysical properties and well defined temperature of the phase change (0^oC). Special effort was made to properly establish thermal boundary conditions at four non-isothermal walls.

The experimental set-up consists of the convection box, two thermostats, two specially constructed halogen light sources, the frame grabber (IC-PCI ITI), the three chip CCD colour camera (JVC) and three axis stepping motors. The flow field was illuminated with a 2mm thin sheet of white light and observed at perpendicular direction. Both velocity and temperature fields were monitored using Thermochromic Liquid Crystal (TLC) tracers¹. Particle Image Thermometry (PIT), which is based on temperature-dependent reflectivity of TLC, was applied to measure 2-D temperature fields. Particle Image Velocimetry (PIV) was used to evaluate 2-D velocity vectors from tracers displacement. Changing with help of the stepping motors the position and orientation of the illuminating light sheet, the entire flow field could be analysed in successive steps. So far experiments have been performed on water at an initial temperature 0.5^oC. The experiment started when temperature of the two metal walls was simultaneously changed.

Our main interest was directed to collect quantitative information about velocity and temperature fields for the two vertical planes, at the cavity centre and at neighbourhood of the front wall. The flow images were collected periodically every 60s or 120s for approximately two hours. When the temperature difference was applied, a thin layer of ice was formed within several seconds at the cold wall. The thickness of the layer increased with a flat vertical ice-water front moving towards to the hot wall. With passing of time (approx. 10min), convection flow established over the entire water region with one clock-wise and one anti-clockwise recirculation region. The interface exhibited evident curvature (comp. Fig. 1), which strongly depends on the hot wall temperature.

Experimental results were compared with numerical simulations performed using modified 3-D finite difference code ICE3D². Solutions were obtained using a mesh of the size 21x21x21 for the fluid domain and 21x21x11 for the solid domain. The computational model has been designed to simulate, as closely as possible, the specifications and temperatures of the physical experiment. The adiabatic and nonadiabatic thermal boundary conditions at four non- isothermal walls were imposed to check their influence on the flow structure. Furthermore numerical simulations were performed using the 3-D model for wall heat conductivity solving the coupled fluid-solid heat conduction problem.

The computational and experimental results have been found to be generally in a reasonable agreement, except regions close to the bottom wall. Our attempts to elucidate the observed discrepancies and to improve modelling will be presented.

REFERENCES

1. Hiller, W. J., Koch, St., Kowalewski, T.A. & Stella, F. ,Onset of natural convection in a cube, Int. J. Heat Mass Transfer, 36, pp. 3251-3263, 1993.
2. Yeoh, G.H., Natural convection in a solidifying liquid, Ph.D. Thesis, University of New South Wales, Sydney, Australia, 1993.

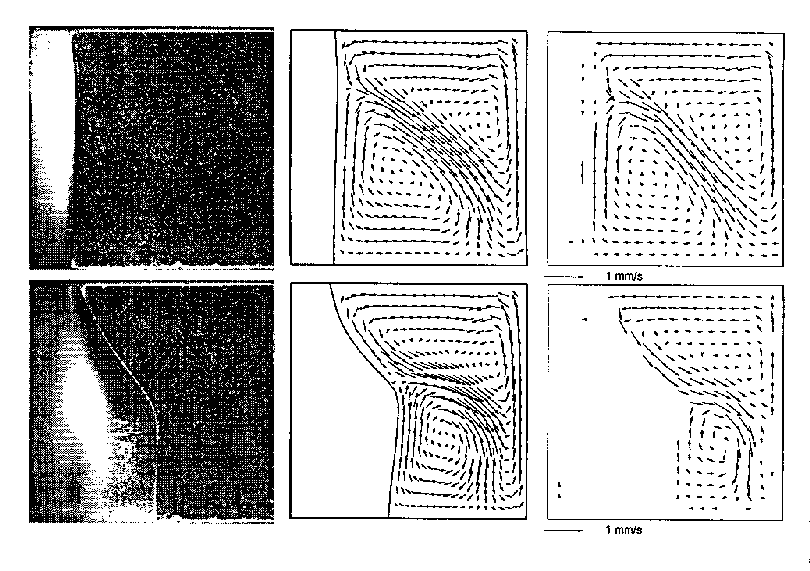
Figure 1. Freezing in the differentially heated cavity at the centre vertical cross-section.

Two time steps: 660s (top row) and 100min (bottom row); Interface images (left), numerical (middle) and PIV measured (right) velocity vectors.