|
Session 14
TURBULENCE
Chairman: R. Shah
PERFORMANCE OF RNG TURBULENCE MODELLING FOR TURBULENT FORCED CONVECTIVE HEAT TRANSFER IN DUCTS
Masoud Rokni and Bengt Sundén
Division of Heat Transfer, Lund Institute of Technology, 221 00 Lund, Sweden
ABSTRACT
This investigation concerns numerical calculation of turbulent forced convective heat transfer and fluid flow in straight ducts using the RNG (Re-Normalized Group) turbulence method.
A computational method has been developed to predict the turbulent Reynolds stresses and turbulent heat fluxes in ducts with different turbulence models. The turbulent Reynolds stresses and other turbulent flow quantities are predicted with the RNG k-e model and the RNG non-linear k-e model of Speziale. The turbulent heat fluxes are modeled by the simple eddy diffusivity (SED) concept, GGDH (Generalized Gradient Diffusion Hypothesis) and WET (Wealth µ Earning x times) methods. Two wall functions are used, one for velocity fields and one for temperature field. The Jayatillika’s P-function is thus abandon. The models are implemented in an arbitrary three dimensional channel.
Fully developed condition is achieved by imposing cyclic boundary conditions in the main flow direction. The numerical approach is based on the finite volume technique with a non-staggered grid arrangement. The pressure-velocity coupling is handled by the SIMPLEC-algorithm. The convective terms are treated by the van Leer scheme while the diffusive terms are handled by the central-difference scheme. The hybrid scheme is used for solving the k and e equations.
The overall comparison between the models are presented in terms of the friction factor and Nusselt number. The secondary flow generation is also of major concern.
Secondary motion of Prandtl’s second kind takes place in non-circular straight ducts in the plane perpendicular to the main flow direction and is turbulence-driven. Secondary motions are of importance since they redistribute the kinetic energy, influence the axial velocity and thereby affect the wall shear stress and heat transfer. A standard linear k-e model does not have the ability to predict secondary flows, but adding non-linear terms into the constitutive relation for the Reynolds stresses allows the model to predict secondary flows without solving additional equations. In order to develop the capability of a non-linear k-e model to predict friction factors and Nusselt numbers in ducts, a new model is presented in this investigation. Speziale’s non-linear k-e model is combined with the RNG (Re-Normalized Group) k-e model. Near the walls, the wall functions are used for both the momentum equations and the temperature field, respectively.
The idea of the dynamic Re-Normalization Group (RNG) is; systematic removal of the small scales of turbulence to a point where large scales are resolvable. To approach this idea the following consideration is necessary; remove the small scales by defining dynamic equations for the large scales and averaging them over an infinitesimal band of the small scales. Yakhot et al (1992) further developed this model and expressed an RNG k-e model which can be used with wall functions and does not need the turbulent viscosity modification. The modification is introduced in the dissipation rate equation instead,
  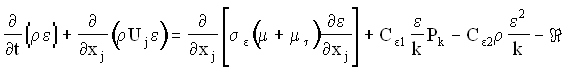 (1) (1)
where s e =1.39, Ce 1 =1.42, Ce 2 =1.68 according to Yakhot et al, 1992. The production term Pk is expressed as
 where where  (2) (2)
and  is defined as
 where where  (3) (3)
In equation (3), h 0 = 4.38 is fixed and b RNG = 0.012 (in applications b RNG can be varied between 0.01 and 0.015, see Yakhot et al (1992)).
A non-linear constitutive relation for the eddy viscosity in incompressible flow proposed by Speziale (1987) is used in this investigation. The Reynolds stresses in this model are determined according to
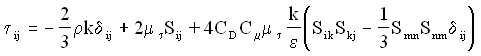
 (4) (4)
and  is the frame-indifferent Oldroyd derivative of is the frame-indifferent Oldroyd derivative of  expressed as expressed as
 (5) (5)
In eq. (4), CD = CE =1.68.
A modified wall function for the temperature field is applied, namely
 (6) (6)
where k t = 0.46 is employed here. For a cold wall and a medium with Pr = 0.72, the value of Bt is set to 2.0 . The point T+ = 5.83 is used to dispose the intersection between the sublayer and the log layer.
The predicted secondary velocity field using the non-linear RNG k-e model is shown in Fig. 1a. Figure 1b shows the streamwise velocity contours predicted by the non-linear RNG k-e model with different b RNG. Due to the presence of the secondary motions the contours are bulged towards the corner. Figure 1b shows that the effect of b RNG is restricted to the region where the secondary velocities are very small (close to the center-line). Stronger bulging is obtained in this region if b RNG is increased. The following calculations have been carried out with b RNG = 0.015.

The average friction factors predicted by this model agree very well with the Blasius correlation. The calculated Nu-numbers obtained by the GGDH and WET concepts are also in decent agreement with Dittus-Boelter correlation. However, the SED underestimates the Nusselt numbers, see Fig. 2.

An important conclusion is that the non-linear RNG k-e model is less grid dependent than the non-linear k-e model without using RNG method if the near wall region is treated by employing wall functions. This conclusion is very important when the RNG method is employed in a wavy duct using wall functions. The number of grid points can thus be decreased and thereby less computational effort is needed.
REFERENCES
- Speziale, C. G., 1987, ”On Non-linear K-l and K-e Models of Turbulence”, J. Fluid Mech., Vol. 178, pp. 459-475.
- Yakhot, V., Orszag, S. A., Thangam S., Gatski, T. B., Speziale, C. G., 1992, ”Development of Turbulence Models for Shear Flows by a Double Expansion Technique”, Phys. Fluids, Vol. A 4, No. 7, pp. 1510-1520.
A NUMERICAL STUDY OF HEAT TRANSFER IN SWIRL FLOWS
A.Smirnov, V.Golovitchev and J.Chomiak
Dept. Thermo and Fluid Dynamics
Chalmers University of Technology
Gothenburg Sweden
INTRODUCTION
Computing heat transport in turbulent swirl flows can be a difficult task given the complexity of recirculation patterns that can arise in such flows1. The standard single closure models are known to perform poorly in predicting swirl flows2, therefore, corrections to the basic model are necessary to account for the effects of swirl. One simple way to introduce these corrections is by using so-called Richardson number based modifications3. These modifications allow to retain the simplicity and efficiency of two-equation models. The disadvantage of this method lies in an empirical coefficient with a rather uncertain value, used to scale the Richardson number corrections.
In this study we performed computation of heat transfer in a turbulent swirl flow through a pipe using a k-e
turbulence model with gradient Richardson number correction4. The value of the empirical constant for the Richardson number was selected from the maximum flow-rate principle5.
CASE STUDY
Experimental data of Kutateladze 6, et al cover the case of heat transfer in a pipe where a swirling jet is entering close to the pipe wall (Fig. 1). Since a strong shear layer is created close to the wall due to such an arrangement it provides a good test case for heat transfer models between the wall and the bulk of the fluid. The inlet tangential velocity component initiates swirling motion in the bulk of the flow downstream of the inlet. There are two basic arrangements considered: in case a apart from the swirling wall jet the main flow is entering the pipe through the axial region; in case b the central axial region is closed and only the wall jet is entering the pipe.

Figure 1. Swirling flow in a pipe:
(a) open central inlet (b) closed central inlet
Flow regime in case a where the central inlet channel is open is similar in character to a simple shear layer flow. There are no recirculation zones in this case and the flow has a parabolic character in contrast to thecase b where a strong central recirculation zone is present and the flow is hyperbolic.
SOLUTION METHOD
The computations were performed using the a k-e
turbulence model model corrected for swirling flow by use of the Richardson number3-4. Computations were performed on a Cartesian grid. The uneven grid spacing was employed so as to resolve the high gradients of the flow field close to the wall-jet inlet. Grid spacings were smallest at the wall-jet inlet and expanded in both radial and axial directions with an expansion coefficient of 1.02.
The value of the Richardson correction constant was selected from the principle of maximum flow-rate7 which in its alternative formulation says that for the given flow-rate the pressure drop should be minimal. One can thus improve predictions by selecting the value of the Richardson constant corresponding to the minimum pressure drop.
RESULTS
Fig. 2 shows the computed flow-field at three different cross-sections within the chamber. The value of Richardson correction constant of 0.003, selected from the principle of maximum flow-rate, gives the best agreement with the experimental data in case b. Case a showed a much weaker sensitivity to the Richardsson constant. Since, strictly speaking, the principle works only for flows close to the critical regime, we would expect it to work better in case b, where the central recirculation pattern is present and, therefore, the critical regime within the chamber exists.
Fig.3 shows predicted wall temperature distribution compared with experimental data. In case a the wall temperature gives the right gradient but the absolute value is shifted by about 10-15oC. This shift could be a result of initial transition behavior close to the inlet. The lack of more detailed data on the heat transfer within the inlet channel did not allow us to compute the temperature increase in this section of the tube. Nevertheless, in case b both the absolute value and the trend of the temperature distribution were predicted very well.
The results show that conventional Richardson number correction techniques may still offer a viable tool for heat transfer computations in turbulent swirl flows.
REFERENCES
- Gupta, A.K., Lilley, D.G. and Syred, N., Swirl Flows, Abacus Press, 1984.
- Gupta, A.K., Beer, J.M., Louis, J.F., Busnaina, A.A. and Lilley, D.G., Flow aerodynamics modeling of an MHD swirl combustor: calculations and experimental verification. Trans. Am. Soc. Mech. Engrs, J.Fluids Engng, 104:385-392, 1982.
- Sloan, D.G., Smith, P.J. and Smoot L.D. Modeling of swirl in turbulent flow systems. Prog.Energy Combust.Sci., 12:163-250, 1986.
- Launder, B.E., Priddin, C.H. and Sharma, B.I. The calculation of turbulent boundary layers on spinning and curved surfaces. Trans. Am. Soc. Mech. Engrs, J.Fluids Engrg, 99:231-239, 1977.
- Smirnov, A.V. and Chomiak, J., Maximum flow principle in swirl flow modeling. Svenska Mekanikdagar, Svenska Nationalkommitten för Mekanik, Luleå 1997.
- Kutateladze, S.S., Volchkov, E.P. and Terekhov, V.I., Aerodynamics and Heat and Mass Exchange in: Bounded Vortex Flows. Academy of Sciences of USSR. Siberian branch. Institute of Thermophysics, Novosibirsk, Russia, 1987.
- J.K. Vennard and R.L. Street. Elementary Fluid Dynamics. John Wiley & Sons, Inc., New York, London, 1975.
a) b) b)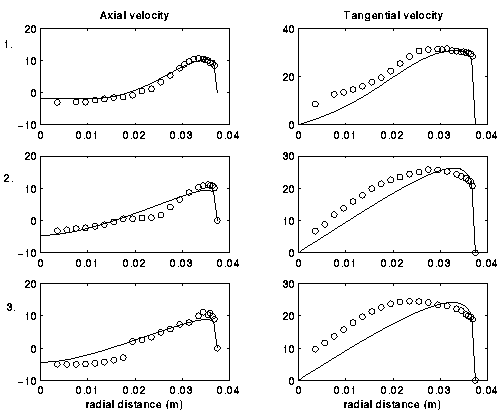
Figure 2. Axial and tangential velocity distributions: (a) open central inlet, (b) closed central inlet.
Axial distances: 1. x=0.046, 2. x=0.136, 3. x=0.246
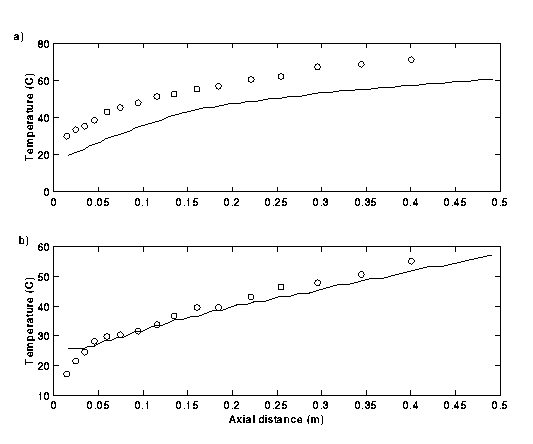
Figure 3. Wall temperature distribution: a) open central inlet, b) closed central inlet
THE FUNCTION OF THE VISCOUS SUBLAYER IN NUMERICAL SIMULATION OF TURBULENCE RECIRCULATING FLOW WITH HEAT TRANSFER
A. Shklyar and A. Arbel
Institute of Agricultural Engineering
A.R.O., The Volcani Center
P.O. BOX. 6 Bet Dagan 50250, Israel
INTRODUCTION
Heat transfer in recirculating flow without buoyancy or mass transfer through the surface was
studied by numerical simulation for the case of separating and reattaching flows downstream of a
backward-facing step. Two-layers  models with modified wall functions were used. This method
yields accurate results with fewer node points within the boundary layer then the low Reynolds
number method (for a backward-facing step, Abe et. al.l used a grid with up to 509xl49 points ).
The standard X smodel for anisotropic eddy viscosity can yield good prediction of the reattachment
point but with a l00x200 grid. Thangam and Speziale2, undoubtedly, grid refinement can alleviate
some problems, but for normal engineering accuracy with many variable parameters it is unsuitable.
The use of a wall funetion allows the effect of the gradient in the vicinity of the wall to be
overcome, and enables empirical information to be introduced. There are many kinds of wall
function - ranging from one dimensional (Wolfstein3) to those including accelerated flow and
turbulent flow on porous flat walls ( Antonia, Zhu and Sokolov4). models with modified wall functions were used. This method
yields accurate results with fewer node points within the boundary layer then the low Reynolds
number method (for a backward-facing step, Abe et. al.l used a grid with up to 509xl49 points ).
The standard X smodel for anisotropic eddy viscosity can yield good prediction of the reattachment
point but with a l00x200 grid. Thangam and Speziale2, undoubtedly, grid refinement can alleviate
some problems, but for normal engineering accuracy with many variable parameters it is unsuitable.
The use of a wall funetion allows the effect of the gradient in the vicinity of the wall to be
overcome, and enables empirical information to be introduced. There are many kinds of wall
function - ranging from one dimensional (Wolfstein3) to those including accelerated flow and
turbulent flow on porous flat walls ( Antonia, Zhu and Sokolov4).
In a two- or three-layer model, (Amano5) there is always a uncertainty about the location of the
boundary between the viscous sublayer and the inner part of the turbulent layer. For equilibrium
flow yV+  11 ( V-boundary of the viscous sublayer). 11 ( V-boundary of the viscous sublayer).
Experimental data on velocity profiles close to the walls for separated and reattaching flows reported
by Davenport6 and Adams and Johnston7 show the yV+ is greatly reduced. It is known that rapid
variations in shear stress normal to the wall can appreciably modify the additive constant in the log
law. Treatment based on relating the sublayer thickness, nondimensionalized by using the near-wall
turbulent kinetic energy, to the local turbulence intensity was used by Ciofalo and Collinsy8 for an
explicit function.
MATHEMATICAL AND PHYSICAL MODEL
An a equation for yv of the form kpl/2yv/v = Rev (Rev=20.4) was proposed by Launder and Spalding9
and was modified to kpl/2yv/v = Rev by Chieng and Launder10; Johnson and Launderll, Launder12
made Rev a linear function of the ratio of the rate of diffusive inflow of turbulent energy to the rate
of turbulent energy dissipation in the sublayer;

the kinetic energy gradient is evaluated on the turbulent side of the viscous sublayer. Time-averaged Navier-Stokes
and energy equations using the high-Reynolds-number C turbulence model proposed by
Launder and Spalding9 were utilized. The Bossinesq viscosity model approximation was used with
the  turbulence model. Inlet profiles for u, turbulence model. Inlet profiles for u,  , ,  are specified for experimental conditions ( Vogel
and Eatonnl3), 2.5 m upstream of the step corner), u is taken from the experimental data and the
corresponding profiles for are specified for experimental conditions ( Vogel
and Eatonnl3), 2.5 m upstream of the step corner), u is taken from the experimental data and the
corresponding profiles for  and and  are computed from model formulated for channel flow. are computed from model formulated for channel flow.
Conditions for velocity, using relationships for  V were
applied at all the walls. Launder and Spalding9 proposed
that close to the wall there is a linear viscous sublayer, but
for first point at the wall we use a numerical solution of the
momentum equation without any assumptions concerning
pressure gradient, velocity gradient along the surface, etc.
The turbulence length scale is based on the distance from
the wall; the mean generation rate of turbulence energy PaV,
and the mean dissipation rate V were
applied at all the walls. Launder and Spalding9 proposed
that close to the wall there is a linear viscous sublayer, but
for first point at the wall we use a numerical solution of the
momentum equation without any assumptions concerning
pressure gradient, velocity gradient along the surface, etc.
The turbulence length scale is based on the distance from
the wall; the mean generation rate of turbulence energy PaV,
and the mean dissipation rate  V are taken from Launder12.
Rev was constructed as a function of ß=Pav V are taken from Launder12.
Rev was constructed as a function of ß=Pav av, Rev=ReO + (Reo-Rer)( av, Rev=ReO + (Reo-Rer)( 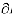 Rev/ Rev/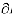 ß). Fig. 1 shows the behavior of the ß
in the function Rev = Reo(1-a exp(-ß2/b2)): ß is unity
downstream of the reattachment point, but in recirculation
zone it is 0.45. Use of the function for Rev was proposed by
Johnson and Launder11 assuming linear extrapolation of the ß). Fig. 1 shows the behavior of the ß
in the function Rev = Reo(1-a exp(-ß2/b2)): ß is unity
downstream of the reattachment point, but in recirculation
zone it is 0.45. Use of the function for Rev was proposed by
Johnson and Launder11 assuming linear extrapolation of the
 v from two points on the boundary of the viscous sublayer
- for example, y+ for reverse flow is 5, but the second point
may lie at 100. v from two points on the boundary of the viscous sublayer
- for example, y+ for reverse flow is 5, but the second point
may lie at 100.

NUMERICAL SOLUTION PROCEDURE
An iterative numerical procedure was applied to the present physical system, by means of code
froml4. The hybrid central/upwind differences were used for the convective terms and a central
difference for the diffusion terms. Upwind differencing was used when the grid Peclet number in
a given direction was greater than or equal to 2; otherwise, central differences were employed. This
procedure incorporates the SIMPLER solution technique of Patankarl5. Poisson's equation for
pressure was solved by the method of successive overrelaxation (SOR). The convergence eriterion
adopted was that the sum of the normalized residuals should be on the order of 1.E-7.
RESULTS
Fig. 2. presents the experimental profile of the Stanton
number (St). Curves for grid with y axis from 60 to 100
practically coincide (only 40 points along x axis).
Furthermore, x axis grid to 200 doesn't affect reattachment
point and curve form. All the calculations demonstrated
here were done on a grid 60x40. Fig. 3 shows the y+ of the
viscous sublayer; a sharp minimum is predicted near the
reattachment point; in the recirculation zone y+ is not higher
than 5, in agreement with the experimental results of
Adams and Johnston7. The wall shear stress distribution
also is well predicted.

REFERENCES
- Abe, K., Kondoh, T. and Nagano,Y. A new turbulent model for predicting fluid flow and heat transfer in separating and reattaching flows - II. Thermal field calculations,Int. J. Heat Mass Trans. vol. 38, pp.l467-1489,1995.
- Thangam, S. and Speziale, C.G. Turbulent flow past a backward-facing step: critical evaluation of two-equation models. AIAA J., vol. 30, pp. 1314-1320,1992.
- Wolstein, M. The velocity and temperature distribution in one-dimensional flow with turbulence augmentation and pressure gradient, Int. J. Heat Mass Trans., vol. 12, pp. 301-318, 1969.
- Antonia, R.A. and Zhu, Sokolov, M. Effect of concentrated wall suction on a turbulent boundary layer, Phys. Fluids 7, pp. 2465-2474,1995.
- Amano, R.S. Development of a turbulence near-wall model and its application to separated and reattached flows, Num. Heat Trans. vol 7, pp. 59-75, 1984.
- Davenport, W.J. Separation Bubbles at High Reynolds Number: Measurement and Computation, Ph. D. Thesis, Dept. of Eng., Univ. of Cambridge, (froms),1985.
- Adams, E.W. and Johnston, J.P. Flow structure in the near-wall zone of a turbulent separated flow, AIAA J., 26, pp. 932-939,1988.
- ciofalo, M. and Collins, M.W.
 predictions of heat transfer in turbulent recirculating flows using an improved wall treatment, Num. Heat Trans.,B,lS, pp. 2I-47, 1989. predictions of heat transfer in turbulent recirculating flows using an improved wall treatment, Num. Heat Trans.,B,lS, pp. 2I-47, 1989.
- Launder, B.E. and Spalding, D.B. The numerical computational of turbulent flow. Comp. Meth. App. Mech. Eng. 3, pp. 269-289, 1972.
- Chieng, C.C. and Launder, B.E. On the calculation of turbulent heat transfer downstream from an abrupt pipe expansion, Num. Heat Trans. ,3, pp. 189-207, 1980.
- Johnston, R.W. and Launder, B.E. Discussion of "On the calculation of turbulent heat transfer downstream from an abrupt pipe expansion", Num. Heat Trans. 5., pp. 493-496, 1982.
- Launder, B.E, On the computation of convective heat transfer in complex turbulent flows, Trans. ASME, 110, pp. 1112-1128,1988.
- Vogel, J.C. and Eaton, J.K. Combined heat transfer and fluid dynamic measurements downstream of a backward-facing step, Trans. ASME,107, pp. 922-929,1985.
- Shklyar, A. Numerical simulation of multiphase flow. Problems in mechanics and applied mathematics. Trans. MFTI, Moscow,1990.
- Patankar, S.V., Numerical Heat Transfer and Fluid Flow, New York, Hemisphere. 1980.
|

