|
Session 8
CONVECTION
Chairman: V. I. Polezhaev
CONVECTIVE HEAT TRANSFER OVER A 3-D BACKWARD FACING STEP
Darrell W. Pepper and David B. Carrington
Department of Mechanical Engineering
University of Nevada, Las Vegas
4505 Maryland Parkway
Las Vegas, NV 89154-4027
INTRODUCTION
A well known benchmark problem for evaluating fluid flow models is flow over a backward facing step. This problem has been examined in considerable detail for 2-D flow1,2; incorporation of heat transfer into the classic problem was assessed in 1992 at the ASME Winter Annual Meeting3.
The reasons for analyzing flow over a backward facing step are the simplicity of the problem, ease of establishing a numerical model, and known (expected) results at various Reynolds numbers. Numerical results by Gartling2 illustrate the use of the backward facing step as an example problem case for assessing outflow boundary conditions. Sohn4 likewise used the backward step problem for evaluating the commercial finite element code FIDAP for laminar and turbulent flows. An international symposium on numerical methods included the backward step with steady isothermal flow conditions as a suggested benchmark problem5. Vradis and Nostrand6 analyzed the flow over a 2-D backward step with the bottom channel wall heated and the top channel wall cool.
Numerical simulations of the fluid patterns over a 3-D step have been conducted by Shih and Ho7, Williams and Baker8, and recently by Chiang and Sheu9. Experimental studies by Armaly et al1 measured the separation and reattachment points for a wide range of Reynolds numbers for the isothermal case. Three-dimensional effects appeared to be significant for Re>400.
PROBLEM DEFINITION
The same geometry and boundary conditions used for the hydrodynamic case by Gartling2, and the experimental investigation conducted by Armaly et al1, are employed in this study. The 3-D channel has an initial height of 0.5 cm and is 12 cm wide, with the top and bottom walls heated at a constant flux of 400 W/m2; the side walls are adiabatic. The flow area suddenly expands into a channel height of H=1.0 cm, as shown in Fig. 1. The velocity and temperature profiles at the step are parabolic and assumed uniform over the width of the channel.

Figure 1. 3-D Step Geometry
The Navier-Stokes and energy equations are given in non-dimensional form as3
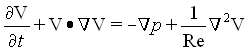 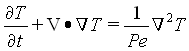
where the Reynolds and Peclet numbers are defined as Re = VH/ n = 100<Re<800 and Pe = VH/a . An explicit, isoparametric finite element scheme is used with Petrov-Galerkin weighting and local h-adaptation to solve the governing equations. In h-adaptation, the mesh refines in regions with the greatest activity, and unrefines where the solution is smooth.
RESULTS
Two-dimensional simulations were first conducted, and results compared with those in the literature1-3. Streamlines and temperature profiles for the 2-D backward facing step are shown in Fig. 2(a-d). The model performed as expected, producing a recirculation zone at the base of the step with a length of 6H, as seen in the streamline pattern shown in Fig. 2(a), which is in close agreement with results from Gartling2 for Re = 800. The 2-D isotherm pattern is seen in Fig. 2(b), and agrees with results obtained by others in the ASME benchmark study3. The h-adapted mesh and velocity vectors are shown in Fig. 2(c), and indicates where the mesh has begun to refine within the top and bottom wall recirculation zones. Figure 2(d) shows the velocity vectors at all nodal points.

Figure 2. Results for 2-D Step
Figure 4 shows the velocity vectors near the midplane of the 3-D backward facing step, and clearly indicates the occurrence of lower and upper (weak) recirculation zones, similar to those predicted by Williams and Baker8 and Chiang and Sheu9. The reattachment length on the lower wall compares with results obtained by Armaly et al1 and Williams and Baker8.

Figure 4. Midplane Velocity Vectors for 3-D Step - Re = 800.
The variation in reattachment length along the bottom wall, at the base of the step, is shown for both 2- and 3-D configurations.

Figure 5. Reattachment Length vs Re
CONCLUSIONS
The h-adapting, finite element algorithm produces results similar to those found in the literature for both 2- and 3-D flow over a backward facing step. Three-dimensional results tend to more correctly match experimental data. Portability of the code permitted computations to be performed on a 166 MHz PC, an SGI O2, and an SGI Origin 2000 parallel computer.
REFERENCES
- Armaly, B. F., Durst, F., Pereira, J. C. F., and Schonung, B., Experimental and Theoretical Investigation of Backward-Facing Step Flow, J. Fluid Mech., Vol. 172, pp. 473-496, 1983.
- Gartling, D. K., A Test Problem for Outflow Boundary Conditions - Flow Over a Backward-Facing Step, Int. J. Num. Meth. Fluids, Vol. 11, pp. 953-967, 1990.
- Blackwell, B. F. and Pepper, D. W., Benchmark Problems for Heat Transfer Codes, HTD Vol. 222, ASME, NY, 89p., 1992
- Sohn, J., Evaluation of FIDAP on Some Classical Laminar and Turbulent Benchmarks, Int. J. Num. Meth. Fluids, Vol. 8, pp. 1469-1490, 1988.
- Gresho, P. M., Seventh Int. Conf. on Num. Meth. in Laminar and Turbulent Flow, Stanford Univ., Palo Alto, CA, July 15-19, 1991.
- Vradis, G. and Nostrand, L., Laminar Flow and Heat Transfer Downstream of a Confined Backward Facing Step Including Variable Viscosity Effects, ASME WAM, Dallas, TX, Nov. 25-30; HTD-157, 1990.
- Shih, C. and Ho, C.-M., Three-dimensional Recirculation Flow in a Backward Facing Step, ASME J. Fluids Eng., Vol. 116, pp. 228-232, 1994.
- Williams, P. T. and Baker, A. J., Incompressible Computational Fluids Dynamics and the Continuity Constraint Method for the Three-Dimensional Navier-Stokes Equations, Num. Heat Transfer Part B, Vol. 29, pp. 137-273, 1996.
- Chiang, T. P. and Sheu, T. W. H., Vortical Flow over a 3-D Backward-Facing Step, Num. Heat Transfer Part A, Vol. 31, pp.167-192, 1997.
RAYLEIGH-MARANGONI CONVECTION IN A POROUS CAVITY
M.Z.Saghir*, M. Hennenberg**, J.C. Legros*** and M.R. Islam****
*U.A.E University, Dept. of Mechanical Eng, Al Ain, U.A.E
** Chimie-Physique, Faculté des Sciences, U.L.B, Belgium
*** Microgravity Research Center, Faculté des Sciences Appliquées, U.L.B, Belgium
**** U.A.E University, Dept. of Chemical & Petroleum Eng., Al Ain, U.A.E
INTRODUCTION
Natural convection in a horizontal porous layer is one of the fundamental problems concerning heat transfer in porous media and has been studied extensively. Kladias and Prasad1 showed that the free convection in porous media is governed by the fluid parameters, namely Rayleigh and Prandtl numbers and the Darcy number (Da). It was demonstrated that the effect of the Darcy number is significant for Da > 10-4. The effect of Prandtl number was found to be quite significant at low values of the fluid Prandtl number (Prf), and is observed to diminish as the Prf increases beyond a value of unity. Bories2 conducted an experiment to study the mechanism of natural convection in a porous cavity. The cavity contained glass bead of equal size and shapes to achieve a porosity of 0,39. It was found that beyond the critical Rayleigh number Rac=4p 2, the flow regime did change from a conductive to a convective case. A convective cell similar to Bénard convection in a clear fluid was observed.
The main objective of this paper is to introduce and study numerically the interaction between the Marangoni convection and the natural convection in a square porous cavity. This numerical approach has been conducted for a Darcy number Da = 9x10-6 and for a porosity f equal to 0,39 in order to simulate the experimental setup close to that of Bories2. The flow is assumed to be Newtonian and in a steady state.
RESULTS AND DISCUSSIONS
The fluid used in our analysis is n-Hexane (C6H14). The finite element mesh consisted of 2100 quadrilateral elements. A finer mesh system was used near the free surface where the Marangoni effect was the most active. The boundary conditions as applied to this model are illustrated in Figure 1. The Rayleigh number Ra was set equal to 3,5x106. Figure 2 displays the stream function contours. This figure shows the presence of four convective cells rotating in different directions. The upper cells rotate in the same manner than the case of microgravity. In particular, the rotation starts from the center of the cavity toward the cavity wall. The two bottom cells rotate in an opposite direction of the upper cells. In particular, the flow takes place from the wall toward the center of the cavity.

Figure 1. Square cavity model and boundary conditions
For that reason, the two diagonal cells have the same flow direction and are joined together as it is displayed in Figure 2.

Figure 2. Stream lines y in the cavity for the Rayleigh-Marangoni case
The emergence of four-cell flow pattern in the Rayleigh-Marangoni problem in porous media has not been reported before to the best of the authors’ knowledge. This observation is reminiscent of the bifurcation phenomenon observed by Islam and Nanadakumar3 who studied mixed convection in porous media. This bifurcation phenomenon was further studied by the same authors, but in the context of flow instability and transition through periodic, quasi-periodic and chaotic flow regimes4. Such investigation in the Rayleigh-Marangoni problem in porous media is underway by the same authors. In the microgravity case, the flow exists only near the free surface5. In the gravity case and in the absence of the free surface, it was found that the flow takes place from the bottom of the cavity to the top. In our case, by including the surface tension effect or the Marangoni convection, a breakaway of these rolls leads to the emergence of four cells of different sizes and directions. Clearly, Marangoni convection enhances the convection in a porous cavity and explains the hexagonal shape of the flow, which were found in the Bories2 experiment.
CONCLUSIONS
In this analysis, a new approach to explore the importance of the surface tension driven flow problem in a porous medium was studied. Marangoni convection in porous media plays the same role as in a fluid in an open duct. However, the magnitude of the velocity is less pronounced in the porous medium convection. The interaction between the Marangoni and the Rayleigh convection lead to the formation of two pairs of counter-rotating cells in the porous cavity. This creates a distinctly different flow characteristic in the Marangoni-Rayleigh case from the one observed in Marangoni convection alone. Marangoni convection showed the formation of only two cells with the loci of the cells pressed close to the free surface of the cavity.
REFERENCES
- N. Kladias and V. Prasad, Natural Convection in Horizontal Porous Layers: Effects of Darcy and Prandtl Numbers, Transaction of the ASME, 926, Vol 111, November 1989.
- S. Bories, Sur les Mécanismes Fondamentaux de la Convection Naturelle en Milieu Poreux, Revue Générale de Thermique, Vol 108(7), pp1377-1402, 1970.
- Islam, M.R. and Nandakumar, K., Multiple Solution for Buoyancy-Induced Flow in Saturated Porous Media for Large Peclet Numbers, ASME Journal of Heat Transfer, Vol 108 (4), p. 866-871, 1986.
- Islam, M.R. and Nandakumar, K., "Transient Convection in Saturated Porous Layers With Internal Heat Sources", Int. J. Heat and Mass Transfer, Vol 33 (1), 151-161, 1990
- M. Hennenberg, M.Z. Saghir, A. Rednikov and J.C. Legros, Porous Media and the Bénard-Marangoni Problem, Transport in Porous Media Journal ,1997, in press.
INSTABILITY IN COMBINED HEAT AND MASS TRANSFER PROBLEMS IN POROUS MEDIA WITH TEMPERATURE DEPENDENT VISCOSITY
M.R. Islam* and M.Z. Saghir**
*Dept. of Chemical and Petroleum Engineering
**Dept. of Mechanical Engineering
UAE University, U.A.E.
INTRODUCTION
Exothermic chemical reactions can influence natural convection effects in a porous medium. This problem finds applications in several disciplines, such as, Chemical Engineering, Geological Engineering, Nuclear Engineering, and others. The combined heat and mass transfer problem in porous media is typical in tubular reactors, oxidation of solid materials in large containers, chemical vapour deposition systems, liquid explosives, and others. Experimental evidence indicates that the viscosity variation with temperature cannot be neglected. Little has been done in the past to investigate the role of viscosity dependence on the temperature in the presence of combined heat and mass transfers.
Only a few previous studies of natural or mixed convection in porous media have focused on studying the case of variable viscosity(1-5). Recently, Dona and Stewart2 have studied the effect of variable viscosity in natural convection in porous media. Lai and Kulacki3 solved boundary layer flow around a vertical surface in porous media. Most of these studied considered linear variation of viscosity with temperature. More recently, Jang and Leu4 presented steady-state results in buoyancy-induced flow of liquids in a porous medium using exponential variation of viscosity with temperature. The same was extended by Rao and Pop5.
In the present work, two-dimensional convection generated and sustained by an exothermic reaction in porous media is studied for the case of temperature-dependent viscosity. Previous studies indicate that chaotic flow can exist for a wide range of parameter values even when the viscosity is assumed to be constant6. A variable viscosity makes the governing equations more difficult to solve. This is particularly complicated when an exponential relationship between viscosity and temperature is assumed5. Previous studies conducted on the topic did not observe any instability because the numerical technique failed to converge for the unstable region. In this paper, we solve the problem of combined heat and mass transfer in a porous medium filled with a fluid of temperature dependent viscosity.
MATHEMATICAL FORMULATION
The transient effects of two-dimensional thermo-chemical convection is considered in this paper. Gatica et al. 7 provided the governing equations in dimensional forms. The flow equations, coupled with the continuity equation is given by

The mass balance equation, in its dimensionless form, is given by,

The energy balance equation is given by,

In order to incorporate the exponential dependence of viscosity on temperature, the following equation is introduced to the flow equation:

This results into an additional constraint for velocity vectors [Rao and Pop, 1994], such that,

In the above equation, s is the stream function, x is the angle of inclination, Ra1 is the thermal Rayleigh number, Ra2 is the concentration Rayleigh number, q is the temperature, a is the aspect ratio, v (u,v) is the velocity vector, C is the concentration, t is time, Da is the Dahmkohler number, B is the adiabatic temperature rise, m* is the viscosity, and x and z are the co-ordinate system. Note that all variables are dimensionless (except m).
The boundary and initial conditions are taken from Gatica et al. [1987]. The governing equations were solved using the Arakawa-Dufort-Frankel scheme that has an accuracy of Dt2 and Dx4, Dz4 (see Ref. 6 for detail).
DISCUSSION AND CONCLUSION
Flow behavior in this system is governed by several conventional parameters, such as, thermal and concentration Rayleigh numbers, Lewis number, Peclet number, aspect ratio, and the angle of inclination. Also, the temperature dependence of viscosity gives rise to another dimensionless parameter that includes the ratio of the viscous forces. Solutions were obtained for a wide range of each of the parameters listed above. Each case reaches chaotic pattern for an increasing value of the thermal or concentration Rayleigh number. However, the routes to chaos are different for different solution branches. These routes are profoundly affected by the magnitude of the dimensionless group that contains the viscosity terms. For higher values of this dimensionless group, periodic and quasi-periodic regimes were extremely short ‘lived’. A detailed study of the frequency of oscillations and power spectrum (FFT analysis) revealed that the instability in this system was reached with little frequency interlocking, as sharp peaks existed even for the chaotic flow regime (while the dimension of chaotic attractors confirmed the existence of chaos). However, as the thermal or concentration Rayleigh numbers were increased, a stable

Fig. 1 Map of Thermal and Concentration Rayleigh Number (m*=1)
steady-state regime re-appeared. The stability regime map was completed for the space of concentration vs. thermal Rayleigh number, thermal Rayleigh no. vs. viscosity dimensionless group, aspect ratio and the order of reaction. For the case of m*=1, the flow regime map is shown in Figure 1. From the patterns for different Rayleigh numbers, it can be seen that points linking each specific pattern results into near straight lines. In other words, the evolution of a regime at a particular thermal Rayleigh number is linearly related to the concentration Rayleigh number. This is not the case when viscosity is considered to be an exponential function of temperature. In those cases, the flow regime maps gave rise to shapes comparable to cusp catastrophe. For most cases, periodic and quasi-periodic solutions were observed in addition to chaotic and, of course, stable solutions.
REFERENCES
- Horne, R.N. and O’Sullivan, M.J., 1978, “Convection in a Porous Medium Heated from Below: The Effect of Temperature Dependent Viscosity and Thermal Expansion Coefficient”, J. Heat Transfer, vol. 100, 448-452.
- Dona, C.L.G., and Stewart, W.E., 1989, “Variable Property Effects on Convection in a Heat Generating Porous Medium”, J. Heat Transfer, vol. 111, 1100-1102.
- Lai, F.C., and Kulacki, F.A., 1990, “The Effect of Variable Viscosity on Convective Heat Transfer along a Vertical Surface in a Saturated Porous Medium”, Int. J. Heat Mass Transfer, vol. 33, 1028-1031.
- Jang, J.Y., and Leu, J.S., 1992, “Buoyancy-Induced Boundary Layer Flow in Liquids in a Porous Medium with Temperature Dependent Viscosity”, Int. Comm. Heat Mass Transfer, vol. 19, 435-444.
- Rao, K.N. and Pop, I., 1994, “Transient Free Convection in a Fluid Saturated Porous Media with Temperature Dependent Viscosity”, Int. Comm. In Heat and Mass Transfer, vol. 21, no. 4, pp. 573-581.
- Basu, A. and Islam, M.R., 1996, “Instability in a Combined Heat and Mass Transfer problem in Porous Media”, Chaos, Solitons, and Fractals, vol. 7, no. 1, pp. 109-123.
- Gatica, J.E., Viljoen, H.J., and Hlaveck, V., 1978, “Influence of Secondary Flows on Stability of Chemically Reacting Systems”, AIChE Journal, vol. 33 (8), pp. 1344-1350.
DIRECT NUMERICAL SIMULATION OF FLOW IN A RIBBED CHANNEL
Odile Labbé , Juliette Ryan and Pierre Sagaut
O.N.E.R.A., BP 72, 92322 Châtillon Cedex, France
The issue of turbine lifetime is an important one, particularly for modern turbines operating at high temperature regimes. A cooling design such as ribs may achieve an improved lifetime and complex mechanisms of heat transfer need to be well studied. In this paper, a direct numerical simulation is presented for a 3-D channel flow with two square ribs on the lower wall. The full unsteady compressible Navier-Stokes equations are solved with an original hybrid finite difference/finite element scheme. The Reynolds number of the simulation is 7 000 based on the bulk velocity at the inlet and the channel height. The present study is mainly to gather better understanding of the unsteady flow behavior in front of the obstacle and in the downstream region, from the rear of the rib to the reattachment point, where significant heat transfer variation is expected.
GOVERNING EQUATIONS
The governing equations of interest are the full unsteady Navier-Stokes equations for a compressible fluid. Considering the conservative form, the equations are written as follows:
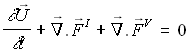
 denote inviscid and viscous fluxes respectively. For numerical stability reasons, the non-linear terms are written in the skew-symmetric form 1-2 The inflow and outflow boundaries are subsonic. The upper wall is adiabatic and the lower one alike the ribs are heated at a uniform temperature. denote inviscid and viscous fluxes respectively. For numerical stability reasons, the non-linear terms are written in the skew-symmetric form 1-2 The inflow and outflow boundaries are subsonic. The upper wall is adiabatic and the lower one alike the ribs are heated at a uniform temperature.
NUMERICAL PROCEDURE
A hybrid finite-difference/finite-element scheme is used for the solution of the previous problem. The finite element scheme uses the Galerkin method with Q1 hexaedral elements to approximate the derivatives on a structured grid. This scheme is applied to all variables as in the Group Finite Element Method 3 and is second-order accurate. For the convective part of the skew-symmetric form, an upwind finite difference scheme (Kawamura 4) is used which is third order accurate.
Time integration used a fully explicit Euler scheme suitable for the treatment of non-linear problems with a large number of discretization points.
RESULTS
The simulation was performed with 321´ 41´ 103 points on the computational domain shown in fig.1. The code has been parallelized on a PARAGON XPS5 computer, with NX library and we used 56 nodes for the computation. The programmation model is that of Single Program Multiple Data, that means each node sees the same program.
The main interest is the unsteady behavior of the flow. The fig.2 shows instantaneous spanwise vorticity contours at three times: t=166, t=168 and t=170. The flow is dominated by many eddies in the neighbourhood of the ribs. Most of these eddies are generated at the front top corner of the ribs and moves behind them as they grow. Fig.3 shows the heat flux on the lower wall and the ribs and two streamwise vorticity surfaces which correspond to the Kelvin-Helmoltz structures. Vortices increase the rate of kinetic energy flux and modify the velocity and temperature profiles and their gradients, so that heat transfer enhancement is important. All primitive variables, their gradient and their fluctuation, together with velocity-pressure and velocity-temperature correlations have been averaged. This data base is very useful to improve the turbulence models. Such a simulation can be used as a tool to understand the physical mechanisms involved. The full paper will describe the relationships between heat transfer, wall shear stress and coherent structure dynamics of the unsteady flows.
REFERENCES
- Lê, T.H. , Troff, B . Sagaut, P. K. Dang-Tran, K. and L. Ta Phuoc, L, PEGASE : a Navier-Stokes solver for direct numerical simulation of incompressible flows". To appear in Int. J. Numer. Methods Fluids.
- Labbé, O. , Lê, T.H. and Dang-Tran, K. , Numerical simulation of separated flow with heat transfer (Ed. C. Taylor, P. Durbetaki) , pp. 597 - 607, Numerical methods in Laminar and Turbulent Flow'95 , Pineridge Press,Swansea,1995.
- Fletcher, C. A. J. , Numerical Computation of Internal and External Flows, John Wiley and Sons 1988.
- Kawamura, T. and Kuwahara, K. , Computation of high Reynolds number flow around a circular cylinder with surface roughness". AIAA Paper 84-0340, 1984 .

Figure 1 : Geometry of computation domain

Figure 2 : Iso-spanwise vorticity at t=166,168 and 170.

Figure 3 : Iso-streamwise vorticity and heat flux at the walls at t=170
|

