POSTER SESSION 2
EFFECTS OF THE RADIATIVE TRANSFER OF THE VAPOR PHASE ON THE BOIL-OFF RATES
A. BENBRIK, M. RIGHI, A ELAHOUEL
National Institut of Hydrocarbons, Boumerdes, ALGERIA.
ABSTRACT
Algeria is one of the greatest producing countries of natural gas . For its export to consumer
countries it is liquified and stored at a temperature of -162oC in a cryogenic storage tanks of a
capacity of 56000 m3, and a pressure slightly greater than atmospheric pressure. Thermal insulation
of these tanks is realized by the perlite or the fiberglass. Despite that, the infiltration of the middle
ambient heat to the inner of the tank remains always present. Consequently the natural liquified gas
evaporates. These vapors are called Boil-off. The maximum boil-off designed is 0.08 % of the total
storage tank volume per day. The stored LNG is a mixture of Methane, and heavy Hydrocarbons
with a weak percentage of nitrogen, these vapors are mainly constiuted of Methane. The Boil-off
represents a sensitive loss. And also affects the physical and chemical properties of the LNG.
Cryogenic storage tanks are never completely flled. Enough vapor space is required to provide
adequate volume boiling. The minimum vapor space is about 1/2% of the total storage volume.
The heat transfer into the portion of the tank above the liquid level is controlled by convection and
radiant cooling on the inside surface; this vapor space heat leak cannot be neglected, or the
calculated Boil-off rate will be substantially low. The volume of the vapor varies accordingly to
the liquid level inside the tank. This vapor which is methane is considered as a semi transparent
media.
Our aim in this work is to study the influence of the transfer heat by thermal radiation of the semi
transparent media on the boil-off rate. The space of the vapor phase is limited by the roof of the
Tank, the cylindrical wall of the liner , and the surface of the liquid surface of LGN. Adjacent
surface temperatures are known, as well as their emissivity coefficients. The surface of the liquid is
considered black.
In this study we have to solve this problem of radiation effect in the semi transparent media by using
Discrete Ordinates Method. Specific cases of different storage parameters such as liquid level and
vapor pressure are taken into account.
Obtained results have confirmed the influence of the thermal radiation on the boil-off rate.
REFERENCES
- Adorjan, A.S., Heat Transfer in LNG Engineering, Hemisphere Publishing Corpration,1991.
- Neil, D., Hashemi, H.T. and Sliepcevich, C.M., Boil-off and Wall Temperatures in Aboveground LNG Storage Tanks, Advances in Cryogenic Heat Transfer, Chemical Engineering Progress Symposium Series.

A THEORETICAL AND EXPERIMENTAL INVESTIGATION OF A RADIATIVE COOLING SYSTEM
Moh'd A. Al-Nimr, Z. Kodah and B.E. Nassar
Mechanical Engineering Department.
J. U. S. T.
Irbid - Jordan
ABSTRACT
A radiative cooling system is built in Irbid-Jordan and utilized to cool
and store fluids by direct radiation to the low effective sky temperature. The
radiative cooling system is built to verify the validity of a mathematical model
proposed to describe the system dynamic thermal behaviour. The constructed,
radiative system has the ability to create a 15 oC reduction in the mean
temperature of a 120 liter capacity storage tank over one night, this implies
that the system can emit 13 MJ / (m2. night) to the sky. It is found that the
theoretical and the experimental predictions of the proposed model are in
good agreement.
EXPERIMENTAL STUDY OF RADIATIVE PROPERTIES OF PARTICLES DURING COAL CONVERSION PROCESS
Anatoly P. NEFEDOV, Olga S. VAULINA, Oleg F. PETROV,. Alex A. SAMARIAN
High Energy Density Research Center,
Russian Academy of Sciences, IVTAN, Moscow, Russia
ABSTRACT
The work described here represents our studies of radiative properties of
pulverized coal particles during conversion process. Experiments on a coal-
fired Meeker burner are detailed. To conduct experiments the novel optical
diagnostic techniques have been used which allowed to measure
temperatures of particles and gas; mean sizes, refractive index and
concentration of particles; optical density, and spectral emissivity of a cloud
of coal parricles. The spectral emissivity and single scattering albedo
measurements have been carried out at the different step of the conversion
process of coal particles. These measurements allowed to make a conclusion
about the contribution of the particle emittance into radiative transfer in the
flow of the combustion products.
APPLICATION OF THE BOUNDARY ELEMENT METHOD IN RADIATION
Ryszard A. Bialecki, Lukasz Grela*
Institute of Thermal Technology, Silesian Technical University, Gliwice, Poland1
*Power Plant Laziska, Poland
1. INTRODUCTION
The paper shows two new applications of the Boundary Element Method (BEM) in heat radiation:
solving radiation transfer problems in emitting absorbing media and solving heat transfer problems in
solids containing self irradiating portions of the boundaries.
BEM is a numerical technique used to solve boundary value problems1. The field of application of
this method is similar to the field methods as FEM and FDM. While in the field methods the original
differential equations are being discretized, the objects discretized in BEM are integral equations.
The latter are obtained by applying the reciprocity theorem to the boundary value problem at hand.
As a discretization technique of integral equations BEM is an efficient tool to handle integral equations
of heat radiation. Moreover, because the singular behaviour of the kernels arising in equations
of radiation and that of standard BEM are the same2, the application of BEM in radiation is
straightforward.
2. HEAT RADIATION IN PARTICIPATING MEDIA
Hottel's zoning method is a well established tool of solving radiative heat transfer problems. Several
improvements of the classic zoning technique have been reported in the literature3. It has been shown
recently2, that the original Hottel's formulation can be interpreted as a Galerkin discretization of the
integral equations of heat radiation.
From the standpoint of the numerical implementation, the main drawback of he zoning technique is
its long computer running time. Other inherent difficulty of this approach is the poor accuracy of
numerical evaluation of matrix entries (exchange areas). Geometries that stray form purely
rectangular or cylindrical are difficult to handle by zoning techniques. Boundary Element Method (BEM)
offers simple way to bypass all these difficulties.
Consider a volume V filled with participating medium and bounded by a surface S being a diffuse
emitter and reflector of radiation. For such a configuration the governing equations of heat radiation
link four functions: blackbody emissive power eb[T] of the surface S, blackbody emissive power of
the medium eb[Tm] filling the domain, radiative heat flux qr on the bounding surface, and radiative
heat source qvr within the domain. Energy balance on an differential surface element yields the first
governing integral equation2
 (1) (1)
where: b- radiosity, 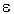 - emissivity, a- absorption coefficient, - emissivity, a- absorption coefficient, 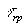 - transmissivity between current
point r and observation point p, K, K1 - kernel functions proportional to |r-p|-2. Surface and volume
integrals arising on the right hand side of Eq. 1 will be denoted as I and Iv, respectively. Similar
balance written for differential volume of the medium produces the second governing equation. This
equation is explicit in radiative heat sources. As numerical treatment of both governing equations is
analogous, only the first one will be discussed here. - transmissivity between current
point r and observation point p, K, K1 - kernel functions proportional to |r-p|-2. Surface and volume
integrals arising on the right hand side of Eq. 1 will be denoted as I and Iv, respectively. Similar
balance written for differential volume of the medium produces the second governing equation. This
equation is explicit in radiative heat sources. As numerical treatment of both governing equations is
analogous, only the first one will be discussed here.
The classic zoning discretization of Eq. 1 requires calculation of two types of double integrals: over
a product of two surface zones and over a product of a surface and a volume zone. For 3D problems
this means that four and five dimensional integrals should be evaluated. The dimensionality of inte-
gration can be reduced by two when instead of applying Galerkin technique, nodal collocation is
used. The idea behind this approach is to require that Eq. 1 is fulfilled for a set of nodal points. Ad-
ditional acceleration of computations can be achieved by converting the volume integral arising in
Eq. 1 into a surface integral of a line integral. This can be accomplished by carrying out the integra-
tion in spherical coordinate frame. The volume integral assumes then a form
 (2) (2)
where  denotes integration along a line connecting r and p. denotes integration along a line connecting r and p.
To carry out the surface integration arising in integrals Is and Iv the values of the kernel function K
at a set of quadrature nodes should be known. This set of points is the same for both integrals. Additionally,
both integrands contain a line integral. In the case of Is it is the transmissivity and in the
case of Iv it is the integral in braces in Eq. 2. Both line integrals can be evaluated analytically. To
do this, the medium is subdivided into cells and constant (but different) values of temperature and
absorption coefficient is assumed within each cell. To carry out the integration three quantities
should be known for each cell: the length of the ray within a given cell, the temperature of the cell
and its absorption coefficient. All these quantities are calculated when discretizing the surface integral
Is. Thus, all quantities needed to discretize the volume integral Iv are already calculated when
processing the surface integral Is. The most time consuming procedure of the Hottel's zoning
method, ie., the discretization of the volume integrals is performed in BEM almost for free.
Poor accuracy of numerical integration has been reported in the literature on zoning technique.
Some authors propose to use regression or Lagrangian multipliers to correct the values of the calculated
entries of the zoning matrices3. It has been shown2 that the reason of the error is the singular
behaviour of the kernel functions K. The accuracy of numerical integration of such functions is poor
because the polynomial interpolation used in quadratures cannot approximate singular variation of
the integrand. The same problem has been encountered in standard BEM, where several techniques
of handling this difficulty have been developed. The method used in the present work is based on a a
priori error estimate of the Gaussian quadrature. This error is expressed in terms of the relative dis-
tance of the surface element and the observation point4. It can be therefore checked, before the integration
is carried out, whether the accuracy is below the prescribed threshold. If not, the surface
element is subdivided into two subelements. The error of integration is then estimated for these subelements.
If necessary, the subelements are further subdivided. The subdivision strategy is based on
the octree algorithm used in computer graphics to store images. When using BEM, the conservation
relations on the entries of the matrices can be satisfied with practically arbitrary accuracy, limited
solely by the finite representation of numbers in the computer.
3. COUPLING OF HEAT RADIATION, CONVECTION AND CONDUCTION
Self irradiation of concave portions of boundaries makes the solution of the corresponding heat conduction problem
difficult. In realistic problems, this portion of the boundary exchanges heat both by
radiation and convection. The energy conservation equation for such boundary can be written as
q = h(T - Tf) + qr where q- conductive heat flux, Tr- temperature of the radiating concave
boundary, f- temperature in the core of the fluid, h- heat transfer coefficient. Radiative heat flux
qr is a solution of an integral equation, the boundary condition at concave boundary is therefore non
local. It depends on temperatures of all points of the boundary that can be seen from a given point.
Heat conduction problems in bodies containing radiative cavities require simultaneous solution of the
differential equation of heat conduction and the integral equation of heat radiation. Steady state heat
conduction in bodies consisting of several subregions of different conductivity are analyzed. The
surface of the cavity is a gray and diffuse emitter and reflector of radiation. The medium filling cavities
formed by concave boundaries is transparent to radiation. BEM is used in both conductive and
radiative portions of the analysis.
BEM discretization of heat condition problem yields a set of algebraic equation having a form HT = Gq + Zqr
. Where H, G and Z known matrices of constant coefficients.Vectors T, q and
qr contain nodal values of boundary temperatures, conductive and radiative heat fluxes, respectively.
Discretized equation of heat radiation has an appearance Aeb[Tr]+Bqr. A and B are known
matrices of constant coefficients, vector eb stores nodal values of blackbody emissive powers at
points placed on the radiating concave surface.
Equations of heat conduction and radiation are coupled by the presence of the radiative heat fluxes
and temperatures at radiating boundaries. An efficient strategy of solving these sets has been developed.
The first step is to eliminate the radiative heat fluxes from radiation and conduction equations
using static condensation. The next step is the elimination of all unknowns except the temperatures
of the radiating surfaces. The eliminations are carried out using a direct linear equations solver. The
resulting nonlinear set of equations has the minimum possible number of unknowns. Newton Raphson
solver proved to be a very efficient tool of solving the final set of equations. The technique has
been extended to handle nonlinear material properties.
REFERENCES
- Banerjee, P.K., Boundary Element Methods in Engineering, McGraw Hill, London, 1994
- Bialecki, R.A., Solving Heat Radiation Problems Using the Boundary Element Method, Computational Mechanics Publications, Southampton and Boston, 1993.
- Howell, J.R., Thermal radiation in participating media: the past, the present, and some possible futures. J. Heat Transf. Vol.110, No.4, pp 220-1229, 1988.
- Bialecki, R.A., Dallner, R. and Kuhn, G., Minimum distance calculation between a source point and a boundary element, Eng. Anal. Bound. Elem., Vol. 12, No.12, pp 211-218, 1994.
1 Financial support of the Polish Committee of Scientific Research under grant T10B01411 is gratefully acknowledged herewith
APPLICATION OF NARROWBAND MODEL TO STUDY THE GAS PHASE RADIATIVE EFFECTS ON THE BURNING OF A SOLID FUEL
Hasan Bedir and James S. T'ien
Department of Mechanical and Aerospace Engineering
Case Western Reserve University, Cleveland, Ohio 44106, USA
ABSTRACT. Gas phase radiative effects on the burning of a solid fuel (PMMA) in a stagnation
point flow geometry are investigated using a statistical narrowband model. Flame profiles
calculated with and without the gas phase radiation are presented.
1. INTRODUCTION
Radiative heat transfer changes the temperature field in a flame and this modifies flame
properties such as thickness and extinction boundaries and species production because of strong
coupling between chemical kinetics and temperature field. Therefore accurate modeling of radiation
is necessary [1]. Narrowband models are considered to be the most accurate radiation
treatment of nongray gases like carbondioxide and water vapor except for the line by line method.
In this paper coupled system of mass, momentum, energy and radiative transport equations are
solved numerically to show the effect of gas phase radiation on the burning of a solid fuel.
2. MATHEMATICAL MODEL
An axisymmetric stagnation point configuration is adopted for the solid fuel laminar diffusion
flame analysis. The combustion model, with one step second order gas phase chemical reaction
and a one step Arrhenius solid pyrolysis reaction, is similar to that described in [2, 3]. A radiative
source term is added to the energy equation and the surface energy balance is modified to take
into account the gas phase radiation.
The flame is assumed to be an infinite planar medium between two black walls, one at the solid
fuel temperature and the other at ambient temperature. The thermodynamics properties are
assumed to vary only with the direction perpendicular to the walls (y). Carbon dioxide, water
vapor and fuel vapor are the only participating gases considered, soot radiation is neglected.
Radiative source term in the energy equation is calculated from nongray radiative transport
equation for an absorbing and emitting medium written in terms of mean transmittance over a
narrowband [4]. A statistical narrowband model with an exponential tailed inverse line strength
distribution [5] is used to calculate transmittance of CO2 and H2O. Mean band parameters
data, generated by Soufiani and Taine from their line by line calculations [6] using HITRAN
92 database, are employed. Statistical narrowband model parameters of MMA vapor are taken
from [7]. Transmittance of nonisothermal and inhomogeneous medium is approximated by the
transmittance of an equivalent isothermal and homogeneous medium (Curtis-Godson approx.).
The radiative transport equation is discretized according to SN discrete ordinates method (20
direction Gaussian quadrature) and solved numerically to obtain radiative heat flux and its
divergence. These values are used in the combustion model to calculate the temperature and
species profiles which are coupled back to the radiative transport equation. This iterative
procedure is repeated until the solution is converged.

Figure l: Effect of gas phase radiation on temperature and species partial pressures. PMMA burning in air, stretch rate is 10 s-1.

Figure 2: Spectral heat flux to the fuel surface and ambient.
3. RESULTS
Fig. 1 shows the effect of gas phase radiation on the burning of PMMA in air for the case with
stretch rate (velocity gradient of the air jet) of 10 s-l. When the gas phase radiation is included
the maximum flame temperature is lower (7%). The reaction zone where oxidizer and fuel meet
and reacts moves closer to the fuel surface, hence there are less products at the ambient side of
the flame. Fuel burning rate, determined through a surface pyrolysis law, is a function of the
net heat flux at the fuel surface. Since the flame temperature is lower, conduction heat flux to
the surface is decreased when the gas phase radiation is included. However the radiation from
the flame to the surface makes up for this decrease and the burning rate is 4% larger for this
particular flame. The spectral radiation heat fluxes are shown in Fig. 2. Surface radiative heat
loss (qw+) and ambient radiation (qe-) are blackbody radiations at corresponding wall and ambient
temperatures. The contributions of various gas bands to the flame radiation to the surface (qw-)
and flame radiation to ambient (qe+) can be seen from the flgure. The largest contribution is by
the strong 4.3  CO2 band followed by MMA vapor bands. CO2 band followed by MMA vapor bands.
The authors acknowledge the support by NASA Microgravity Science and Applications Division grant NAG3-1046
4. REFERENCES
- Rhatigan, J.L., Bedir, H., T'ien, J.S., Gas phase radiative effects on the burning and extinction of a solid fuel, Combust. and Flame, in press.
- T'ien, J.S., Combust. and Flame, Vol.65, pp 31-34,1986.
- T'ien, J.S. et al, Combust. and Flame, Vol.33, pp 55-68, 1978.
- Kim, T.K., Menart, J.A., and Lee, H.S., J. Heat Transf., Vol.ll3, pp 946-951, 1991.
- Malkmus, W., J. Opt. Soc. Am., Vol.57, pp 323-329, 1967
- Soufiani, A. and Taine, J., Int. J. of Heat and Mass Transf., Vo1.40, p 987,1997.
- Park, S.H., Stretton, A.J., Tien, C.L., Combust. and Flame, Vol.62, pp 257-271, 1988.
NUMERICAL SIMULATION OF RADIATIVE-CONVECTIVE INTERACTION IN NOZZLES OF LASER PLASMA ACCELERATORS
S. T. Surzhikov
Institute for Problems in Mechanics Russian Academy of Sciences, Moscow, Russia
Laser Plasma Accelerator (LPA) is defined as a Laval nozzle, inside which gas is heated
up by means of laser radiation (Fig.l).

Fig.l Scheme ot the Laser Plasma Accelerator
In the study a radiative mode of LPA is investigated. Distinctive feature of the radiative
mode of LPA is the fact that cold gas overfilling on laser plasma is heated up to temperature
of unitary ionization by means of own thermal radiation of laser plasma.
The 2D radiative gas-dynamic model of LPA is developed, in which selective radiating
heat exchange of laser plasma with environment is taken into account. The governing
equation of the gas flow in the plane Laval nozzle are the Navier-Stokes equations, mass and
energy conservation equations, heat radiative and laser radiative transfer eduations:

are the density, specific internal energy,
pressure, velocity components along x and y axes, respectively; Wx,g, Wy,g are the group heat
radiative flux eomponents along x and y axes; Ug is the group density of heat radiative
energy,  are the spectral and group radiative intensities; index b denotes
characteristics of a black body; are the spectral and group radiative intensities; index b denotes
characteristics of a black body;  is the direction of radiation propagation, is the direction of radiation propagation,  is the element
of solid angle; kg is the group absorption coefficient, is the element
of solid angle; kg is the group absorption coefficient,  is the laser radiation absorption
coefficient; is the laser radiation absorption
coefficient;  are the heat conductivity coefficient and dynamic viscosity coefficient; are the heat conductivity coefficient and dynamic viscosity coefficient;  is
the specific heat at constant volume; eo is the specific internal energy at the temperature To;
yL(x) is conventional boundary of laser beam. The group functions (fg = kg, Ug, Wx,g, Wy,g) are
obtained by the following integration of the corresponding spectral functions
(fw = kw, Uw, Wx,w, Wy,w): is
the specific heat at constant volume; eo is the specific internal energy at the temperature To;
yL(x) is conventional boundary of laser beam. The group functions (fg = kg, Ug, Wx,g, Wy,g) are
obtained by the following integration of the corresponding spectral functions
(fw = kw, Uw, Wx,w, Wy,w):  , where , where  is the g-th wavenumber scale range. The
total radiative heat flux is obtained by the following summation: is the g-th wavenumber scale range. The
total radiative heat flux is obtained by the following summation:  , where Ng is
the number of spectral groups. , where Ng is
the number of spectral groups.
The multigroup model of the group absorption coefficient kg is calculated at the atmospheric
pressure in the temperature region 300-20000 K with the temperature step  T= 200 K. The 18
spectral groups are taken into account in the spectral region 2000-150000 1/cm. The
thermophysical properties T= 200 K. The 18
spectral groups are taken into account in the spectral region 2000-150000 1/cm. The
thermophysical properties 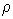 (T), (T),  (T) , and equilibrium composition of heated air are
calculated at the same temperature points. (T) , and equilibrium composition of heated air are
calculated at the same temperature points.
The numerical scheme used to calculate the steady-state solution via a pseudotransient
formulation is based on a second order finite difference discretization of the flux gradients
and a separate time-integration method. The full implicit schemes are used for solution of all
equations. The typical results of the calculations are shown on Fig.2.
It is necessary to stress that the problem under consideration is the strongest self-consistent
problem when temperature and gas dynamic distributions are developed each from other. And
the radiative heat transfer processes are of primary importance in determining the gas
dynamically fields inside the Laval nozzles of the LPA.

Fig.2 The isotherms (dashed lines) in the curvilinear coordinate system and distribution of the temperature along the x-axis (line with crosses) in the symmetry plane (the scale on the right, the temperature in kK) in a subsonic Laval nozzle at PL=30 kW/cm and uo=3 m/sec. The laser radiation and gas flow are directed from left to right
MODELING OF HEAT AND MOISTURE TRANSFER IN THIN CAPILLARY-POROUS MATERIALS UNDER HIGH INTENSITY HEATING BY RADIATION
R.Sh. Enalejev, W.A. Katchalkin
Department of Cybernetics, Kazan Chemical Technological University, Russia
INTRODUCTION
Investigation of heat and moisture transfer into thin capillary-porous materials under high intensity
heating by radiation has both theoretical and practical value in solving of many problems in such
spheres as heat protection of aerocosmic construction [1], intensification of drying processes [2],
determination of high intensity heating mechanism [3].
However, mechanism of interior mass and energy transfer into thin materials accompanied by phase
transformation is still insufficiently known, because it is difficult to measure the field of potential
transfer.
Mathematical description of transfer process circumscribe the system of nonlinear differential
equations of parabolic type. Complicacy of equations and absence of sufficient data on process
characteristics causes insuperable mathematical difficulties during the solution of compatible heat and
mass transfer equations.
That is why we suggest the simplified mathematical models for investigation of interaction processes
of high intensity radiation with thin capillary-porous materials. Construction of models is based on
the mathematical simulation method.
HEAT AND MASS TRANSFER MODEL
The results of mathematical modeling of heat and moisture transfer process in wet textile materials
under pulsed radiant heating are presented in this paper. Adequacy of mathematical model to
experimental data was determined according to parameters which characterize joint heat and
moisture transfer: temperature of sample, loss of sample mass due to radiation, heat balance of
heating process of material and moisture evaporation.

Figure1. Model of heat and moisture transfer
As it is shown on figure 1, the process of vigorous vaporization of moisture on the whole body of
the sample begins just from the very start of radiation process. The process of ebullition of moisture
begins when the temperature on the surface is about 85°C. Under further heating the ebullition
border moves deep down the material, the rate of deepening depends on intensity of radiation,
moisture - content, thermophysical and optical properties of material. Ebullition border divides
material into dry and wet zones. Depending on heating intensity temperature of deep layers behind
the mobile border may mount to the temperature of ebullition, and this causes the advent of the
second mobile border.
Ebullition zone is observed between the two mobile borders; due to vigorous vaporization an excess
pressure arises here. Under the influence of pressure gradient molar flows of vapour and free water
are formed. The movement of free water in high temperature zone is accompanied by its further
evaporation.
Preliminary calculations have shown that diffusion flows of heat and moisture are negligible.
MATHEMATICAL FORMULATION
To determine the temperature fields and moisture content it is necessary to solve the system of
nonlinear differential equations of heat conductivity with volumetrical source of heat, mobile borders
of phase transition and equation of moisture conductivity.
Absence of data on pressure gradient excludes the possibility of solving the equation of moisture
conductivity in its classical formulation [4].
That is why we suggest expressing the rate of evaporation in the equation of moisture conductivity
through the part of absorbed radiation energy spent on evaporation of moisture. It is possible to
realize such an approach by introducing of differential Cossovitch criterion
 (1) (1)
which (for differential volume) characterizes the ration of heat spent on evaporation -Jm(u,x) to heat
absorbed by wet material due to radiation Q(u,x).
Then we can present the equation of energy mathematical formulation in the following way
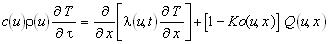 (2) (2)
CONCLUSIONS
- The mathematical model adequately describing the process of heat and moisture transfer in thin capillary-porous materials under the influence of intense light radiation is presented.
- The main mechanisms of inner heat and moisture transfer are determined by mathematical modeling method and their quantitative estimation is also carried out.
- The usage of high temperature sources of radiation can increase the rate of drying tens times as much in comparison with other ways of intense heating
REFERENCES
- Al. Kuryachii . Evalution of system efficency of radiation-evaporating heat protection of flying apparatus. // Mechanics of liquids and gases, 1995, pp. 24-36.
- Chen and D. Pei. A mathematical model of drying processes. // Int. J. Heat Mass Transfer. Vol. 32. ? 2 ,1989,pp 297-310.
- M.D.Mikhailov. Exact solution of temperature and moisture distribution in a porous half-space with moving evaporation front, Int. J. Heat Mass Transfer 18,1975, pp 797-804 .
- A.V.Luikov. Systems of differential equations of heat and mass transfer in capillary-porous bodies. Int. J. Heat Mass Transfer 18, 1975, pp 1-14.
NUMERICAL SIMULATION OF THERMAL STRESSES TAKING PLACE IN SEMITRANSPARENT MATERIALS UNDER LASER RADIATION.
Katasonov A.A., Kokurina G.P., Rumynsky A.N.,
Russia, Kaliningrad, Moscow Region, TsNIIMASh
One of the reasons of materials destruction under laser radiation is occurrence
of thermal stresses due to non-uniform material heating. Investigations of thermal
stresses in opaque and transparent materials were carried out in a lot of works, this
being not so for semitransparent materials because in this case it is necessary to take
into account additionally the process of radiation/conduction heat transfer in
scattering media.
In this work ìn non-connected thermal elasticity approximation we consider
thermal stresses induced by continuos laser radiation in semitransparent materials
with due regard for consumption and scattering of both falling radiation and that from
heated material.
We consider a cylinder of elastic-isotropic uniform material. Axisymmetrical
radiation flux with Gaussian intensity radius distribution, reaching its stationary
regime at some characteristic time to falls on its face surface along the normal.
The complete set of equations describing thermal elastic effect of laser
radiation upon semitransparent material includes equations of radiation/conduction
energy transfer (energy transfer equation and parabolic heat conduction equation with
a source member) and equations of thermoelasticity.
We suppose that the radiation energy transfer equation is valid for this media,
semitransparent material is a grey media with transparent boundaries, and all
materials characteristics are temperature independent.
The consideration of radiation transfer may be divided into two independent
problems:
- radiation transfer due to falling laser one;
- radiation transfer due to that from heated material.
The calculation of radiation transfer due to falling laser one should be carried
out in the most thorough way because of its mono-direct character, so the radiation
energy transfer equation in exact formulation should be used. We write this equation
in the integral form and use Monte-Carlo method local estimators with Calos'
modification) for the calculation of radíation consumption for the established regime
of laser beam.
The diffusion approximation of radiation energy transfer equation may be
used for the calculation of radiation transfer due to that from heated material for
every time moment.
The appearance of other equations is obvious.
The solution of the whole problem may be divided into following independent
stages:
- the consumption of radiation due to falling laser one is calculated once for the established regime;
- the calculation of radiation/conduction heat transfer for selected time period;
- the calculation of thermal stresses for chosen time moments.
It is very convenient to use the finite elements method for the solution of
equations of heat conduction and thermoelasticity and for the calculation of
absorption of radiation from heated material.
The calculations were carned out for specimens of hypothetical ceramics with
both radius R and thickness L equal to 1 cm, energy flux in the beam centre
Fo=1.5 kWt/cm2, beam effective radius ro=0.2 cm. At calculations we varied
specimen optical length  and single-scattering albedo qe . and single-scattering albedo qe .
Analysis of calculations results shows that thermal stresses distribution
significantly depends on optical parameters of sernitransparent materials. First of all
thìs effect manifests itself in behaviour of axial component of stress tensor  up to
change of sign. up to
change of sign.
BASE RADIATION HEAT TRANSFER DURING OPERATION OF ROCKET ENGINES
Rumynsky A.N., Katasonov A.A., Osipov V.A., Pugatchev V.A.
Russia, Kaliningrad, Moscow Region, TsNIIMASh
The problem of vehicle base heating due to thermal radiation of exhaust
gaseous and two-phase jets (solid fuel engines) is known to be important for design of
rockets heat protection. Determination of radiation from such jets is rather difficult
and includes some separate problems:
- calculation of exhaust gaseous or two-phase jets from nozzle exit and determination of its parameters (pressure, temperature, chemical composition of gas mixture, thermal and phase state of condensed particles);
- calculation of gas emission and optical properties of particles (absorptíon and scattering coeff cients and phase function);
- determination of radiation heat lux to the vehicle elements.
Each of these problems enumerated in turns requires the preliminary decision
of a number of questions. For example, the calculation of two-phase flow in nozzle
must be carried out before determination of parameters in exhaust jet. Furthermore
the thermodynamic calculation in combustion chamber should be obtained.
The calculation of thermal radiation from some gaseous jets for multi-nozzle
engine is a separate problem. The interaction of supersonic jets will take place during
vehicle operation. This interaction leads to appearance of the shock waves and, as a
result, to the existence of regions in which gas will have high temperature and
pressure. These regions are main sources of thermal radiation to the vehicle elements.
The problems mentioned above are solved using a number of simplifications
which have to meet the following demands:
- the method must allow to calculate radiation flux with acceptable accuracy (for engineer applications);
- the program must allow to carry out calculations at the acceptable time.
Because of these demands some questions are artificially simplified. For
example, non-equilibrium chemical reactions in gas phase are excluded, particles are
considered to be monodisperse, wave interaction between gas jets is calculated using
oblique shock formulae, etc.
The programs for determination of radiation characteristics from gaseous or
two-phase jet use three large modules:
- "INIT" - calculation of equilibrium gas mixture in nozzle and so, determination the initial condition for next modules;
- "JET" - calculation of two/single - phase flow in axisymmetrical jet flow parameters, extended into flooding flow (Godunov's method is used);
- "RAD" - determination of radiation heat flux to arbitrary point of vehicle base (Ruminsky's undetermined coefficients method is used for the calculation of radiation transfer in scattering media, Reardon's line model for the gas emittance and Mie' theory for particles emittance are used.
The comparison of the results of these calculations with available
experimental data shows good agreement.
|

