SESSION 2
NEW APPROACHES FOR MODELING RTE
Chairman: M. Lallemand
WAVELETS AND THE DISCRETE ORDINATES METHOD IN THE SOLUTION OF THE RADIATIVE HEAT TRANSFER EQUATION
Yildiz Bayazitoglu, Ye Wang, Bryan Y. Wang
Department of Mechanical Engineering and Materials Science
Rice University, Houston, USA
ABSTRACT. Nongray radiative heat transfer through an absorbing, emitting, and nonscattering
medium between two infinite parallel heated plates is analyzed. The discrete ordinates method
(DOM) is combined with the wavelet method to evaluate spectral dependence. The results for the
case of radiative equilibrium are given and compared with those obtained by other methods.
NEW DISCRETE P1 - APPROXIMATION APPROACH TO SOLUTION OF RADIATIVE TRANSFER EQUATION IN MULTIDIMENSIONAL AND COMPLEX DOMAINS
V.S. Yuferev, M.G. Vasil'ev, E.N. Kolesnikova
A.F. Ioffe Physical -Technical Institute of Russian Academy of Sciences,
St. Petersburg, Russia
Advanced method for the solution of multi-dimensional radiative heat transfer problems is
developed. The basic idea of the method lies in construction of the special subdivision of the total
solid angle surrounding an arbitrary point into a set of smaller solid angles (cells) and in
representation of radiation intensity in each solid angle by P1 -approximation. Similar approach was
suggested for the first time thirty years ago in Ref. [1] as applied to neutron transport problem and
then later independently in Refs. [2-3] for solution of radiant transport equation and has shown
excellent results in solving different 1-D radiative heat transfer problems. The close approach has
been used in Ref. [4] for mitigation of ray-effect in neutron transport problems. The essence of the
proposed method can be formulated by the following way.
Let us divide the total solid angle surrounding an arbitrary point into M smaller solid angles in such
a manner that  where cells where cells 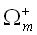 , , 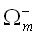 are symmetric to each other relative to the
center of a unit sphere, while the radiant intensity in each solid angle are symmetric to each other relative to the
center of a unit sphere, while the radiant intensity in each solid angle  is given by an expression
analogous to P1 -approximation (for simplicity the grey radiation is considered): is given by an expression
analogous to P1 -approximation (for simplicity the grey radiation is considered):
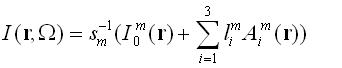 (1) (1)
where  are the direction cosines and are the direction cosines and  . Radiant transport equation is satisfied in the
mean over each elementary cell and the system of the second order partial differential equations with
respect to the local zeroth- or first moments of radiation intensity are derived in rectangular and
cylindrical coordinates. Subdivision of a unit sphere [1] can be carried out by different ways. The
simplest one consists in the arrangement of . Radiant transport equation is satisfied in the
mean over each elementary cell and the system of the second order partial differential equations with
respect to the local zeroth- or first moments of radiation intensity are derived in rectangular and
cylindrical coordinates. Subdivision of a unit sphere [1] can be carried out by different ways. The
simplest one consists in the arrangement of  in such a manner that its boundaries coincide with
the coordinate lines of spherical coordinate system. On the other hand, in our approach the
elementary solid angles in such a manner that its boundaries coincide with
the coordinate lines of spherical coordinate system. On the other hand, in our approach the
elementary solid angles  can depend on spatial coordinates, that is, can be varied from point to
point. The latter is one of the main advantages of the proposed method because permits to take into
account the specific features of the problem under consideration and thus to get required accuracy
using quite coarse angular partitions. Note that both approaches [1,4] do not offer such possibility. It
is shown that if the subdivision does not depend on spatial coordinates, the coefficients Ajm are
determined from the following system of equations can depend on spatial coordinates, that is, can be varied from point to
point. The latter is one of the main advantages of the proposed method because permits to take into
account the specific features of the problem under consideration and thus to get required accuracy
using quite coarse angular partitions. Note that both approaches [1,4] do not offer such possibility. It
is shown that if the subdivision does not depend on spatial coordinates, the coefficients Ajm are
determined from the following system of equations
 (2) (2)
where  , while R>mn and Hilnq are expressed through the zeroth and second
moments of scattering phase function, while the zeroth moments I0m are connected with Ajn in the
following manner , while R>mn and Hilnq are expressed through the zeroth and second
moments of scattering phase function, while the zeroth moments I0m are connected with Ajn in the
following manner

The boundary conditions to Eq. (2) in the case of the diffuse reflection take the form
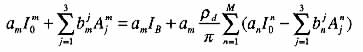
where
 , , 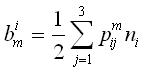
On the other hand, in the case of axisymmetric problems the spatially variable subdivisions have to be
used. In particularly, introducing at the surface of a unit sphere the set of lines 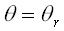 and and  , ( , (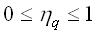 )
, where )
, where 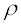 is normalized radial coordinate and is normalized radial coordinate and  are the polar and
azimuth angles of a spherical coordinate system, the following set of equations relative to I0rq are
obtained (here for simplicity the scattering is absent) are the polar and
azimuth angles of a spherical coordinate system, the following set of equations relative to I0rq are
obtained (here for simplicity the scattering is absent)
 (3) (3)
where I0,irq is normalized to srq and signs "+" and "-" correspond to different values of i. In this
case the coefficients srq, p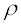 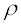 rq and p rq and p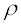 zrq turn out to be dependent on radial coordinate zrq turn out to be dependent on radial coordinate 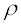 . .
As examples, the radiative transfer in a plane layer of absorbing and linear scattering media and
radiative heat transfer in a circular cylinder with specularly reflective side surface have been
considered. In latter case we have used the spatially dependent subdivision with respect to both
angle  and and  in order to take into account the phenomenon of the total inner reflection. This gave
possibility at the first time to calculate the radiative heat transfer in the optically dense circular
cylinder of finite length with transparent specular side surface. Some attention was given also to the
application of the proposed method to the calculation of radiative transfer in a non-participating
media. in order to take into account the phenomenon of the total inner reflection. This gave
possibility at the first time to calculate the radiative heat transfer in the optically dense circular
cylinder of finite length with transparent specular side surface. Some attention was given also to the
application of the proposed method to the calculation of radiative transfer in a non-participating
media.
REFERENCES
- Lebedev V.I., PNI- Equations, J. Numer. Math. and Math. Physics, Vol. 7, No. 4, pp 813-824, 1967 (in Russian).
- Yuferev V.S., Generalization of Differential Approximation for Calculation of Radiative-Conductive Heat Transfer in a Rectangular Enclosure with Transparent Specularly Reflective boundaries, High Temperature, Vol. 33, pp 961-967, 1995 (in Russian).
- Yuferev V.S. and Vasil'ev M.G., New Approach to Solution of Radiant Transport Equation, submitted to publication in JQSRT.
- Briggs L.L., Miller W.F., and Lewis E.E., Ray-Effect Mitigation in Discrete Ordinate-Like Angular Finite Element Approximation in Neutron Transport, Nuclear Sci. and Eng., Vol. 57, pp. 205-217, 1975.
|

